python树的孩子链存储结构
...........................................................................................................................................................
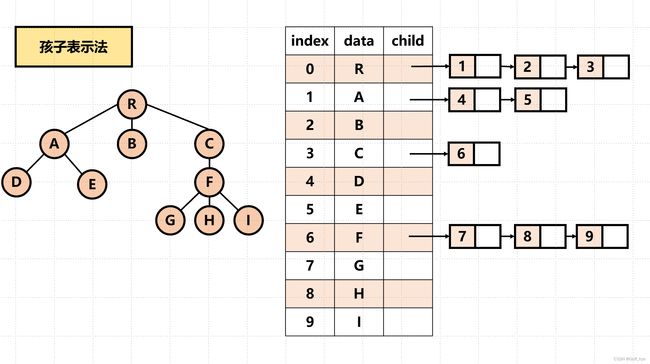
树的孩子链存储结构是一种树的存储方式,它使用孩子兄弟表示法来表示树的结构。在这种存储结构中,树的每个节点都有一个指向其第一个孩子的指针和一个指向其下一个兄弟的指针。这样,可以通过这些指针来表示树的层次结构和节点之间的关系。
...........................................................................................................................................................
具体来说,对于每个节点,可以使用一个结构体来表示,其中包括节点的数据域以及指向其第一个孩子和下一个兄弟的指针。通过这种方式,可以轻松地遍历树的节点,查找节点的孩子和兄弟节点,以及进行其他操作。
...........................................................................................................................................................
..........................................................................................................................................................
树孩子链存储结构在一些应用中比较常见,特别是对于动态树结构的表示和操作,它可以提供比较灵活的存储方式,并且可以节省一定的存储空间。然而,由于需要额外的指针来表示孩子和兄弟节点的关系,可能会增加一定的存储开销,并且在一些操作上可能会比较复杂。因此,在选择树的存储结构时,需要根据具体的应用场景和需求来进行选择。
...........................................................................................................................................................
代码:
...........................................................................................................................................................
class Node():
def __init__(self,data=None):
self.data=data
self.next=None
class stree():
def __init__(self):
self.data=[]# 存储节点类
# 传入结点进入存储的列表结构
def creat(self,arr):# 将节点类创建并传入
for i in range(len(arr)):
p = Node(arr[i])
self.data.append(p)
# 建立节点和节点之间的关系
def creat_s(self,i,j):#i为建立节点的下标,j为连接下标
p = self.data[i]
while p.next!=None:
p = p.next
q = Node(self.data[j].data)
p.next=q
# 遍历操作
def display(self):
for i in range(len(self.data)):
if i==0:
print(self.data[i].data,end=' ')
p = self.data[i].next
while p!= None:
print(p.data,end=" ")
p = p.next
print()
# 添加结点建立联系
def add(self,i,e):# i为e的父节点下标
# 将新节点添加进存储结构的操作
q = Node(e)
self.data.append(q)
# 将新节点和对应i节点建立关系的操作
p = self.data[i]
while p.next != None:
p = p.next
c = Node(e)
p.next = c
# 删除对应i结点下标值为e的结点(方法要求不能删除父结点)
def delx(self,i,e):
p = self.data[i]
while p.next.data!=e and p.next!=None:
p = p.next
p.next=p.next.next
# 找到对应i结点下标值为e的结点,对其修改为值n_e
def change(self,i,e,n_e):
p = self.data[i]
while p.data!=e and p!=None:
p = p.next
if p!=None:
p.data=(n_e)
# 查找对应i结点下标值为e的结点
def find(self,i,e):
p = self.data[i]
while p.data != e and p != None:
p = p.next
if p != None:
return p
a = stree()
a.creat(["A","B","C"])
a.creat_s(0,1)
a.creat_s(0,2)
a.display()
# a.add(0,'D')
# a.display()
# a.delx(0,'D')
# a.display()
# a.change(0,"C",'E')
# a.display()
# print(a.find(0,"E").data)...........................................................................................................................................................
孩子链存储结构相对于其他树的存储结构,具有一些优势:
1. 灵活性:孩子链存储结构可以很容易地表示不规则的树形结构,因为每个节点只需存储其孩子节点和兄弟节点的指针,而不需要预先知道树的深度或者每个节点的孩子个数。
2. 节省空间:相对于其他存储结构,孩子链存储结构可以节省一定的空间,因为它不需要为每个节点都存储孩子节点的个数,只需存储指向孩子节点和兄弟节点的指针。
3. 动态性:孩子链存储结构适合表示动态树结构,因为它可以方便地插入或删除节点,而不需要移动整个树的结构。
4. 方便的遍历和操作:通过孩子链存储结构,可以方便地遍历树的节点,查找节点的孩子和兄弟节点,以及进行其他操作,如搜索、插入、删除等。
孩子链存储结构在某些情况下具有更好的适用性和效率,特别是对于动态树结构的表示和操作。然而,它也有一些缺点,比如可能会增加一定的存储开销,并且在一些操作上可能会比较复杂。因此,在选择树的存储结构时,需要根据具体的应用场景和需求来进行选择。
...........................................................................................................................................................
Guff_hys_python数据结构,大数据开发学习,python实训项目-CSDN博客