78. 子集_39. 组合总和_46. 全排列

总结：

for(int i = begin; i < nums.length; i++) {
	dfs(i+1)  // 1,2,3; 2,3; 3  回溯过后，也要接着向后 78.子集
}

for(int i = begin; i < nums.length; i++) {
	dfs(i) // 1,1,2; 2,2,3,4;... 元素可以重复，全局不重复靠顺序,即回溯时for的i++  39.组合总和
}

for(int i = 0; i < nums.length; i++) {
	if(!used[i]) {
		dfs(depth+1,)  // 元素不重复靠used,  全局不重复靠顺序,即回溯时for的i++ ，46. 全排列
	}
}

不同：
每种元素只出现一次：for(int i = begin,) path.add(nums[i]); dfs(nums,i+1)
每种元素出现次数不限制：for(int i = begin,) path.add(nums[i]); dfs(nums,i)

相同：

• 不重复，即即[1,2] [2,1]算一种，按顺序添加元素，可以不重复
  for(int i = begin; i < nums.length; i++); 当回溯到上一层时，上一层之前的选过的就不能选，因为i会++；从上一次选的后一个元素开始选。
  其实是：按顺序取，只会出现[1,2]，最终答案只会出现[1,2]这个答案。

• 48全排列，for(int i = 0; ) 每次不会从i+1开始选，而是三个都可以选，used保证不重复

• 保证全局不重复，都是采用一个思想，for(int i = ) 回溯到上一层后，之前选的不选，

每种元素值出现一次，不同顺序算重复：78子集
- for循环和没有for循环，进入下一层i+1,和index+1的注意点。
每种元素出现多次，不同顺序算重复：39.组合总和
- 48全排列，用used保证

横向比较

nums = [1,2,3,4,5] nums.length = 5;
第一种情况：参考78.子集
要求：每种元素最多只能出现一次；不重复(按顺序添加元素，可以不重复)，即[1,2] [2,1]算一种；列出所有组合

• 每一层有多个选择，for

• 回溯，向上弹一层，需要丢失这一层的元素，path.pop()；

• 为保证不重复性，需要保持顺序。对应：dfs(nums,index,path,res);
  path.add(nums[i]);dfs(nums, i+1,path,res); --> for(int i = begin) index = index+1；

• 每到达一个节点，path都是满足要求的。对应：在for里面res.add(new ArrayList(path));

• 回溯到上一层时，上次到达这层选择就能再选了，需要从他后一个开始选择；对应：dfs(nums,index,path,res);
  path.add(nums[i]);dfs(nums, i+1,path,res); --> for(int i = begin) i = i++;

---

第二种情况：
要求：

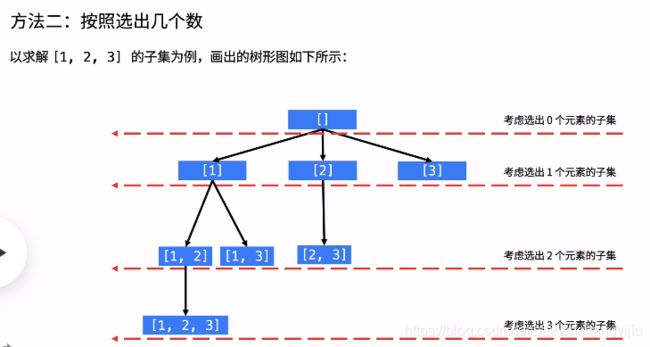
78. 子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        // 第一层：nums.length个选择 
        // 按顺序深入下一层，
        // 回溯时，之前选择的不选择

        List<List<Integer>> res = new ArrayList<>();
        Deque<Integer> path = new ArrayDeque<>();
        dfs(nums, 0, path, res);
        return res;
    }


    private void dfs(int[] nums, int begin, Deque<Integer> path, List<List<Integer>> res) {
        res.add(new ArrayList(path));

        for(int i = begin; i < nums.length; i++) {
            path.addLast(nums[i]);
            dfs(nums, i+1, path, res);
            path.removeLast();
        }
    }
}

public class Solution {

    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        int len = nums.length;
        if (len == 0) {
            return res;
        }
        Stack<Integer> stack = new Stack<>();
        dfs(nums, 0, len, stack, res);
        return res;
    }

    private void dfs(int[] nums, int index, int len,
                     Stack<Integer> stack, List<List<Integer>> res) {
        if (index == len) {
            res.add(new ArrayList<>(stack));
            return;
        }
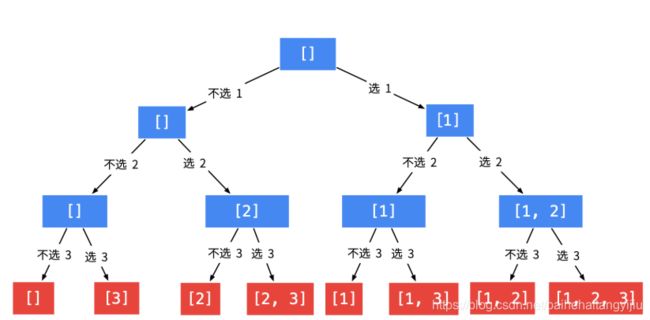
        // 当前数可选，也可以不选

        // 不选，直接进入下一层
        dfs(nums, index + 1, len, stack, res);

        // 选了有，进入下一层
        stack.add(nums[index]);
        dfs(nums, index + 1, len, stack, res);
        stack.pop();
    }

}

作者：liweiwei1419
链接：https://leetcode-cn.com/problems/subsets/solution/hui-su-python-dai-ma-by-liweiwei1419/

---

---

39. 组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

所有数字（包括 target）都是正整数。
解集不能包含重复的组合。
示例 1：

输入：candidates = [2,3,6,7], target = 7,
所求解集为：
[
[7],
[2,2,3]
]
示例 2：

输入：candidates = [2,3,5], target = 8,
所求解集为：
[
[2,2,2,2],
[2,3,3],
[3,5]
]

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
    
        List<List<Integer>> res = new ArrayList<>();
        Deque<Integer> path = new ArrayDeque<>();

        dfs(candidates, 0, target, path, res);
        return res;
    }


    private void dfs(int[] nums, int begin, int target, Deque<Integer> path, List<List<Integer>> res) {

        if(target < 0) {
            return;
        }

        if(target == 0) {
            res.add(new ArrayList(path));
            return;
        }

        for(int i = begin; i < nums.length; i++) {
            path.addLast(nums[i]);
            dfs(nums, i, target - nums[i], path, res);
            path.removeLast();
        }
    } 
}

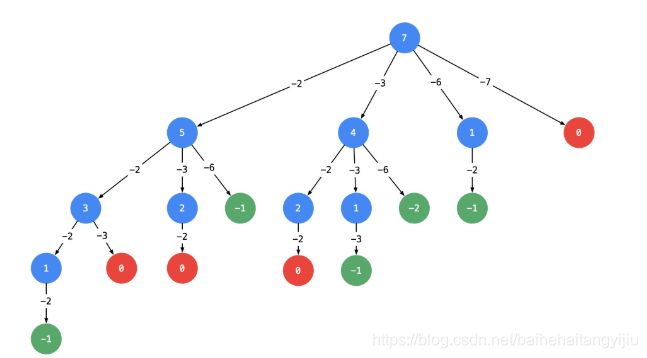
剪枝：

根据上面画树形图的经验，如果 target 减去一个数得到负数，那么减去一个更大的树依然是负数，同样搜索不到结果。基于这个想法，我们可以对输入数组进行排序，添加相关逻辑达到进一步剪枝的目的；

排序是为了提高搜索速度，对于解决这个问题来说非必要。但是搜索问题一般复杂度较高，能剪枝就尽量剪枝。实际工作中如果遇到两种方案拿捏不准的情况，都试一下。

public class Solution {

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> res = new ArrayList<>();
        if (len == 0) {
            return res;
        }

        // 排序是剪枝的前提
        Arrays.sort(candidates);
        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates, 0, len, target, path, res);
        return res;
    }

    private void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> res) {
        // 由于进入更深层的时候，小于 0 的部分被剪枝，因此递归终止条件值只判断等于 0 的情况
        if (target == 0) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = begin; i < len; i++) {
            // 重点理解这里剪枝，前提是候选数组已经有序，
            if (target - candidates[i] < 0) {
                break;
            }
            
            path.addLast(candidates[i]);
            dfs(candidates, i, len, target - candidates[i], path, res);
            path.removeLast();
        }
    }
}

---

---

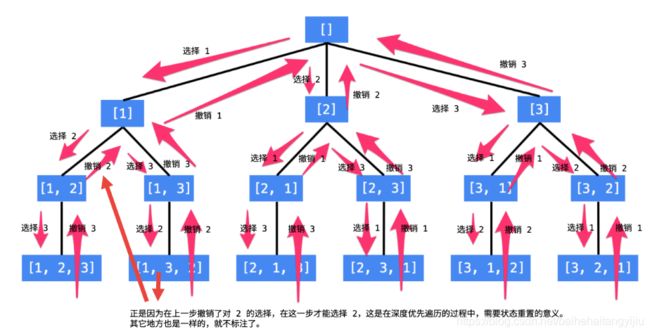
46. 全排列

给定一个 没有重复 数字的序列，返回其所有可能的全排列。
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

class Solution {
    public List<List<Integer>> permute(int[] nums) {
       // 元素不能重复，used取过了，就不能再取了，当到达叶子节点时，添加结果
       // 没有顺序，即[1,2,3] [2,3,1]是不同的：即每一层都要遍历所有元素，不能按顺序取for(int i = 0)
       // 为了保证整体不重复，要顺序举例，for(int i = 0; i++)


       List<List<Integer>> res = new ArrayList<>();
       Deque<Integer> path = new ArrayDeque<>();

        boolean[] used = new boolean[nums.length];

       dfs(nums, 0, path, used, res);
       return res; 
    }


    private void dfs(int[] nums, int index, Deque<Integer> path, boolean[] used, List<List<Integer>> res) {
        if(index == nums.length) {
            res.add(new ArrayList(path));
            return;
        }

        for(int i = 0; i < nums.length; i++) {
            if(!used[i]) {
                used[i] = true;

                path.addLast(nums[i]);
                dfs(nums, index+1, path, used, res);
                path.removeLast();
                used[i] = false;
            }
        }
    }
}