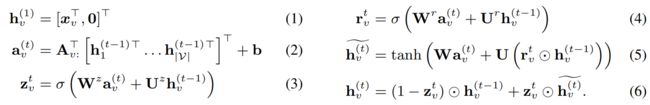GGNN:GATED GRAPH SEQUENCE NEURAL NETWORKS
论文
相较于之前的文章,模型最大的修改即为,使用门控循环单元并且将网络的展开循环控制在一个固定的次数。
一个可达模型:
例如网络需要在给定一个图的情况下,判断节点s是否可达节点t:
模型初始化:
设 定 N o d e A n n o t a t i o n s { x s = [ 1 , 0 ] T x t = [ 0 , 1 ] T x v = [ 0 , 0 ] T ( v ≠ s o r t ) 每 个 节 点 h v = [ x v , 0 ] 即 将 n o d e a n n o t a t i o n 填 充 后 , 将 剩 余 部 分 全 部 设 置 为 0 设定Node Annotations\left\{\begin{array}{l} x_s=[1,0]^T\\ x_t=[0,1]^T\\ x_v=[0,0]^T(v\neq s \ or \ t )\end{array}\right.\\ 每个节点h_v=[x_v,0]即将node \ annotation 填充后,将剩余部分全部设置为0 设定NodeAnnotations⎩⎨⎧xs=[1,0]Txt=[0,1]Txv=[0,0]T(v=s or t)每个节点hv=[xv,0]即将node annotation填充后,将剩余部分全部设置为0
在计算时只需输入s节点的表示作为第一个参数,t的表示为第二个参数,使得传播矩阵在(0,0)位置的值为1即可
由此,在此模型中我们将节点标签作为附加输入。
GGNN
A ∈ R D ∣ V ∣ × 2 D ∣ V ∣ A ∈ R^{D|V|×2D|V|} A∈RD∣V∣×2D∣V∣
A v : ∈ R D ∣ V ∣ × 2 D : v 在 A 对 应 的 两 列 A_{v:} ∈ R^{D|V|×2D}:v在A对应的两列 Av:∈RD∣V∣×2D:v在A对应的两列
a v ( t ) ∈ R 2 D a^{(t)}_v ∈ R^{2D} av(t)∈R2D包含从两个方向的边激活
等 式 1 是 隐 藏 节 点 的 表 示 。 等 式 2 是 通 过 输 入 和 输 出 边 在 图 的 不 同 节 点 之 间 传 递 信 息 的 步 骤 , 参 数 取 决 于 边 的 类 型 和 方 向 。 等式1是隐藏节点的表示。\\ 等式2是通过输入和输出边在图的不同节点之间传递信息的步骤,参数取决于边的类型和方向。 等式1是隐藏节点的表示。等式2是通过输入和输出边在图的不同节点之间传递信息的步骤,参数取决于边的类型和方向。
其 中 : σ ( x ) = 1 / ( 1 + e − x ) l o g i s t i c s i g m o i d f u n c t i o n , ⊙ e l e m e n t − w i s e 乘 法 \color{red} \tiny 其中:σ(x) = 1/(1 + e−x) \ logistic \ sigmoid \ function, \odot \ element-wise乘法 其中:σ(x)=1/(1+e−x) logistic sigmoid function,⊙ element−wise乘法
我们最初尝试了一种普通的递归神经网络风格的更新,但在初步实验中,论文发现这种类似GRU的传播步骤更有效。
输出
对于每个节点的输出仍然可以使用函数 o v = g ( h v ( T ) , x v ) o_v=g(h_v^{(T)},x_v) ov=g(hv(T),xv)
对于graph-level的输出可以使用以下方法: