【算法】NOIP2003神经网络

题目描述

        人工神经网络（Artificial Neural Network）是一种新兴的具有自我学习能力的计算系统，在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。对神经网络的研究一直是当今的热门方向，兰兰同学在自学了一本神经网络的入门书籍后，提出了一个简化模型，他希望你能帮助他用程序检验这个神经网络模型的实用性。

        在兰兰的模型中，神经网络就是一张有向图，图中的节点称为神经元，而且两个神经元之间至多有一条边相连，下图是一个神经元的例子：

神经元〔编号为1）

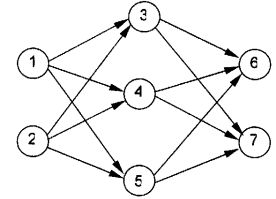
        图中，X1—X3是信息输入渠道，Y1－Y2是信息输出渠道，C1表示神经元目前的状态，Ui是阈值，可视为神经元的一个内在参数。神经元按一定的顺序排列，构成整个神经网络。在兰兰的模型之中，神经网络中的神经无分为几层；称为输入层、输出层，和若干个中间层。每层神经元只向下一层的神经元输出信息，只从上一层神经元接受信息。下图是一个简单的三层神经网络的例子。

兰兰规定，Ci服从公式：

（其中n是网络中所有神经元的数目）

        公式中的Wji（可能为负值）表示连接j号神经元和 i号神经元的边的权值。当 Ci大于0时，该神经元处于兴奋状态，否则就处于平静状态。当神经元处于兴奋状态时，下一秒它会向其他神经元传送信号，信号的强度为Ci。

        如此．在输入层神经元被激发之后，整个网络系统就在信息传输的推动下进行运作。现在，给定一个神经网络，及当前输入层神经元的状态（Ci），要求你的程序运算出最后网络输出层的状态。

输入描述:

第一行是两个整数n（1≤n≤200）和p。

接下来n行，每行两个整数，第i＋1行是神经元i最初状态和其阈值（Ui），非输入层的神经元开始时状态必然为0。

再下面P行，每行由两个整数i，j及一个整数Wij，表示连接神经元i、j的边权值为Wij。

输出描述:

包含若干行，每行有两个整数，分别对应一个神经元的编号，及其最后的状态，两个整数间以空格分隔。 仅输出最后状态非零的输出层神经元状态，并且按照编号由小到大顺序输出！ 若输出层的神经元最后状态均为0，则输出 NULL。

示例1

输入

5 6
1 0
1 0
0 1
0 1
0 1
1 3 1
1 4 1
1 5 1
2 3 1
2 4 1
2 5 1

输出

3 1
4 1
5 1

思路

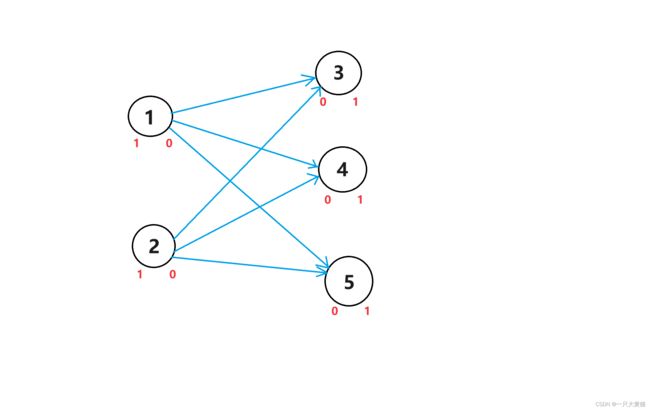
根据样例我们可以得到一张图：（边权均为1）

其中入度位0的点为输入点，出度为0的点位输出点。

只有当上一层的点全部遍历之后才会遍历下一层的点，因此我们可以先求出该有向无环的拓扑排序。

然后根据拓扑排序一次遍历该图的所有点（例如便利到点1，会遍历所有以点1位直接前驱的点），遍历点1之后，3、4、5的状态均为1，遍历点2之后3、4、5均为2，将所有输出点的状态减去阈值，就为最终状态。

（拓扑排序在我之前的文章中有介绍，在此就不多赘述......）

代码 

#include
using namespace std;
const int N = 200 * 200 + 10;
int n,m;
int h[N],ne[N],e[N],w[N],idx;
int dist[N],u[N];
int in[N],out[N];
bool flag[N];

void add(int a,int b,int c)
{
    e[idx] = b,ne[idx] = h[a],w[idx] = c,h[a] = idx ++;
}

void top_sort()
{
    queue q;
    for(int i = 1; i <= n; i ++)
        if(!in[i]) q.push(i);

    while(!q.empty())
    {
        int t = q.front();
        q.pop();
        for(int i = h[t]; ~i ;i = ne[i])
        {
            int j = e[i];
            in[j] --;
            if(dist[t] > 0) dist[j] += w[i] * dist[t];
            if(in[j] == 0)
            {
                q.push(j);
            }
        }
    }
}

int main()
{
    memset(h,-1,sizeof h);
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)
    {
        int a,b;
        cin >> a >> b;
        u[i] = b;
        if(a == 0) dist[i] = a - b;
        else dist[i] = a;
    }

    while(m --)
    {
        int a,b,c;
        cin >> a >> b >> c;
        out[a] ++;
        in[b] ++;
        add(a,b,c);
    }

    top_sort();
    bool f = false;
    for(int i = 1; i <= n; i ++)
    {
        if(!out[i] && dist[i] > 0)
        {
            cout << i << " " << dist[i] << endl;
            f = true;
        }
    }
    if(!f) cout << "NULL" << endl;
    return 0;
}

链接：登录—专业IT笔试面试备考平台_牛客网
来源：牛客网