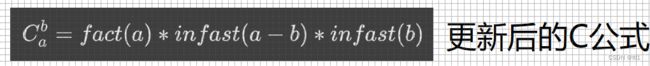C++混合笔记
目录
先上一波最短路模板：
Dijkstra朴素：（链式前向星）
Dijkstra堆优化：(链式前向星)
SPFA:
Bellman_ford
1：Trie
2.并查集
组合数原公式：
组合数公式：
编辑
逆元预处理来求：
在 编辑可用
代码 ：
组合数卢卡斯定理：
代码：
卡特兰数：
编辑
01背包转移方程：
01背包注意事项：
01背包代码：
01背包空间优化版（滚动数组）：
时间复杂度：编辑
完全背包转移方程：
完全背包变量意思：
完全背包朴素版：
复杂度：编辑
完全背包时间优化版：
复杂度：编辑
完全背包时间+空间优化版（滚动数组）：
复杂度：编辑
多重背包转移方程：
多重背包朴素写法（暴力）：
复杂度：编辑
多重背包时间+空间优化版：（二进制分组优化）
复杂度：编辑
多重背包超级优化（单调队列）：
复杂度：编辑
分组背包转移方程：
编辑
分组背包空间优化版：（滚动数组）
线性DP：
经典例题1：数字三角形
最长上升子序列求序列:
先上一波最短路模板：
Dijkstra朴素：（链式前向星）
#include
using namespace std;
const int inf=1e9;
int Begin[100010],Next[100010],To[100010],W[100010],e;
int n,m;
int dis[510];
bool vis[510];
void add(int a,int b,int c)
{
To[++e] = b;
W[e] = c;
Next[e] = Begin[a];
Begin[a] = e;
}
int dijkstra()
{
for(int i=1;i<=n;i++)
{
int pos=-1,mi=INT_MAX;
for(int j=1;j<=n;j++)
{
if(dis[j]>n>>m;
for(int i=1;i<=n;i++)
{
dis[i] = inf;
}
dis[1] = 0;
// vis[1] = 1;
for(int i=1;i<=m;i++)
{
int a,b,c;
cin>>a>>b>>c;
add(a, b, c);
}
cout< Dijkstra堆优化：(链式前向星)
#include
using namespace std;
typedef pair PII;
const int inf=1e9;
int Begin[200010],Next[200010],To[200010],W[200010],e;
int n,m;
int dis[200010];
bool vis[200010];
priority_queue,greater> pq;
void add(int a,int b,int c)
{
To[++e] = b;
W[e] = c;
Next[e] = Begin[a];
Begin[a] = e;
}
int dijkstra()
{
pq.push({0,1});
for(int i=1;i<=n;i++)
{
auto a=pq.top();
pq.pop();
int pos=a.second;
if(vis[pos])
{
continue;
}
vis[pos] = 1;
for(int j=Begin[pos];j;j=Next[j])
{
int v=To[j];
if(dis[pos]+W[j]>n>>m;
for(int i=1;i<=n;i++)
{
dis[i] = inf;
}
dis[1] = 0;
// vis[1] = 1;
for(int i=1;i<=m;i++)
{
int a,b,c;
cin>>a>>b>>c;
add(a, b, c);
}
cout< SPFA:
#include
#include
#include
#include
using namespace std;
const int N = 100010;
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int spfa()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue q;
q.push(1);
st[1] = true;
while (q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
return dist[n];
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
int t = spfa();
if (t == 0x3f3f3f3f) puts("impossible");
else printf("%d\n", t);
return 0;
} Bellman_ford
#include
using namespace std;
struct edge{
int a,b,w;
}ed[10010];
int n,m,k;
int dis[10010],backup[10010];
int bellman_ford()
{
for(int i=1;i<=k;i++)
{
memcpy(backup,dis,sizeof(dis));
for(int j=1;j<=m;j++)
{
int a=ed[j].a,b=ed[j].b,w=ed[j].w;
dis[b] = min(dis[b],backup[a]+w);
}
}
if(dis[n]>0x3f3f3f3f/2)
{
cout<<"impossible";
exit(0);
}
return dis[n];
}
int main()
{
cin>>n>>m>>k;
for(int i=1;i<=m;i++)
{
cin>>ed[i].a>>ed[i].b>>ed[i].w;
}
memset(dis,0x3f,sizeof(dis));
dis[1]=0;
int t=bellman_ford();
cout< 1：Trie
int son[100010][26],cnt[100010],idx;
char s[100010];
void insert(char s[])
{
int p=0;
for(int i=0;s[i];i++)
{
int u=s[i]-'a';
if(!son[p][u])
{
son[p][u] = ++idx;
}
p = son[p][u];
}
cnt[p]++;
}
int find1(char s[])
{
int p=0;
for(int i=0;s[i];i++)
{
int u=s[i]-'a';
if(!son[p][u])
{
return 0;
}
p = son[p][u];
}
return cnt[p];
}2.并查集
int fa[100010];
int find(int x)
{
if(fa[x]!=x)
{
return fa[x] = find(fa[x]);
}
}
int insert(int a,int b)
{
fa[find(a)] = find(b);
}组合数原公式：
组合数公式：
在：
可用递推
代码：
#include
using namespace std;
const int N = 2010, mod = 1e9 + 7;
int c[N][N];
void init()
{
for (int i = 0; i < N; i ++ )
for (int j = 0; j <= i; j ++ )
if (!j) c[i][j] = 1;
else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}
int main()
{
int n;
init();
scanf("%d", &n);
while (n -- )
{
int a, b;
scanf("%d%d", &a, &b);
printf("%d\n", c[a][b]);
}
return 0;
} 逆元预处理来求：
在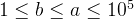 
可用
先定义两个东东：
更新后的组合公式：
代码 ：
#include
using namespace std;
typedef long long LL;
const int N = 100010, mod = 1e9 + 7;
int fact[N], infact[N];
int qmi(int a, int k, int p)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int main()
{
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}
int n;
scanf("%d", &n);
while (n -- )
{
int a, b;
scanf("%d%d", &a, &b);
printf("%d\n", (LL)fact[a] * infact[b] % mod * infact[a - b] % mod);
}
return 0;
} 组合数卢卡斯定理：
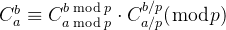
代码：
#include
using namespace std;
typedef long long LL;
int qmi(int a, int k, int p)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int C(int a, int b, int p)
{
if (b > a) return 0;
int res = 1;
for (int i = 1, j = a; i <= b; i ++, j -- )
{
res = (LL)res * j % p;
res = (LL)res * qmi(i, p - 2, p) % p;
}
return res;
}
int lucas(LL a, LL b, int p)
{
if (a < p && b < p) return C(a, b, p);
return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
int main()
{
int n;
cin >> n;
while (n -- )
{
LL a, b;
int p;
cin >> a >> b >> p;
cout << lucas(a, b, p) << endl;
}
return 0;
} 卡特兰数：
01背包转移方程：
01背包注意事项：
-
循环是0~m。
-
下标要注意。
- 每次循环开始时，f[i][j] = f[i][j-1]。
- f[i][j] = f[i][j-1]后要加判断：if(j>=v[i])否则会访问负下标。
- 结合代码会好看一些。
01背包代码：
#include
using namespace std;
int a[1010];
int v[1010],w[1010];
int f[1010][1010];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>v[i]>>w[i];
}
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
f[i][j] = f[i-1][j];
if(j 01背包空间优化版（滚动数组）：
#include
using namespace std;
int a[1010];
int v[1010],w[1010];
int f[1010];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>v[i]>>w[i];
}
for(int i=1;i<=n;i++)
{
for(int j=m;j>=v[i];j--)
{
f[j] = max(f[j],f[j-v[i]]+w[i]);
}
}
cout< 时间复杂度：
完全背包转移方程：
![f_{i,j} = max(f[i][j],f[i-1][j-v_i]*k]+w[i]*k)](http://img.e-com-net.com/image/info8/b3713d95d73c46d0b427f15cc9e1c22d.png){kind=small}
完全背包变量意思：
i:下标
j:容量
k:每个物品个数
完全背包朴素版：
#include
using namespace std;
int a[1010];
int v[1010],w[1010];
int f[1010][1010];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>v[i]>>w[i];
}
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
for(int k=0;k*v[i]<=j;k++)
{
f[i][j] = max(f[i][j],f[i-1][j-v[i]*k]+w[i]*k);
}
}
}
cout< 复杂度：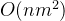
完全背包时间优化版：
#include
using namespace std;
int a[1010];
int v[1010],w[1010];
int f[1010][1010];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>v[i]>>w[i];
}
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
f[i][j] = f[i-1][j];
if(j>=v[i]) f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);
}
}
cout< 复杂度：
完全背包时间+空间优化版（滚动数组）：
#include
using namespace std;
int a[1010];
int v[1010],w[1010];
int f[1010];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>v[i]>>w[i];
}
for(int i=1;i<=n;i++)
{
for(int j=v[i];j<=m;j++)
{
f[j] = max(f[j],f[j-v[i]]+w[i]);
}
}
cout< 复杂度：
多重背包转移方程：
多重背包朴素写法（暴力）：
#include
using namespace std;
int a[1010];
int v[1010],w[1010];
int f[1010][1010];
int s[1010];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>v[i]>>w[i]>>s[i];
}
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
for(int k=0;k*v[i]<=j&&k<=s[i];k++)
{
f[i][j] = max(f[i][j],f[i-1][j-v[i]*k]+w[i]*k);
}
}
}
cout< 复杂度：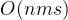
多重背包时间+空间优化版：（二进制分组优化）
#include
using namespace std;
int f[25000];
int v[25000];
int w[25000];
int cnt;
void change(int a,int b,int s)
{
int k=1;
while(k<=s)
{
cnt++;
v[cnt] = a*k;
w[cnt] = b*k;
s-=k;
k*=2;
}
if(s)
{
cnt++;
v[cnt] = a*s;
w[cnt] = b*s;
}
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
int a,b,s;
cin>>a>>b>>s;
change(a,b,s);
}
for(int i=1;i<=cnt;i++)
{
for(int j=m;j>=v[i];j--)
{
f[j] = max(f[j],f[j-v[i]]+w[i]);
}
}
cout< 复杂度：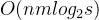
多重背包超级优化（单调队列）：
#include
using namespace std;
int dp[20010],pre[20010],q[20010];
int n,m;
int main()
{
cin>>n>>m;
for(int i=0;i>v>>w>>s;
for(int j=0;jq[head])
{
++head;
}
while(head<=tail&&pre[q[tail]]-(q[tail]-j)/v*w<=pre[k]-(k-j)/v*w)
{
--tail;
}
if(head<=tail)
{
dp[k] = max(dp[k],pre[q[head]]+(k-q[head])/v*w);
}
q[++tail] = k;
}
}
}
cout< 复杂度：
分组背包转移方程：
分组背包空间优化版：（滚动数组）
#include
using namespace std;
int v[110][110],w[110][110];
int s[110];
int f[110];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>s[i];
for(int j=1;j<=s[i];j++)
{
cin>>v[i][j]>>w[i][j];
}
}
for(int i=1;i<=n;i++)
{
for(int j=m;j>=0;j--)
{
for(int k=0;k<=s[i];k++)
{
if(v[i][k]<=j)
{
f[j] = max(f[j],f[j-v[i][k]]+w[i][k]);
}
}
}
}
cout< 线性DP：
经典例题1：数字三角形
题目链接
#include
using namespace std;
int f[1010][1010];
int a[1010][1010];
int main()
{
int n,m;
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
cin>>a[i][j];
}
}
memset(f,-0x3f,sizeof(f));
f[1][1] = a[1][1];
for(int i=2;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
f[i][j] = max(f[i-1][j],f[i-1][j-1])+a[i][j];
}
}
int ret=INT_MIN;
for(int i=1;i<=n;i++)
{
ret=max(ret,f[n][i]);
}
cout< 最长上升子序列求序列:
题目链接
#include
using namespace std;
int a[1010];
int f[1010];
int g[1010];
int main()
{
int n;
cin>>n;
// cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=1;i<=n;i++)
{
f[i]= 1;
g[i]=0;
for(int j=1;j