第十章 算法模式
10.1 递归
递归是一种解决问题的方法,它解决问题的各个小部分,直到解决最初的大问题。递归通常
涉及函数调用自身。
递归函数是像下面这样能够直接调用自身的方法或函数:
function recursiveFunction(someParam){
recursiveFunction(someParam)
}能够像下面这样间接调用自身的函数,也是递归函数:
function recursiveFunction1(someParam){
recursiveFunction2(someParam)
}
function recursiveFunction2(someParam){
recursiveFunction1(someParam)
} 假设现在必须要执行recursiveFunction,结果是什么?单单就上述情况而言,它会一直
执行下去。因此,每个递归函数都必须要有边界条件,即一个不再递归调用的条件(停止点),
以防止无限递归。
10.1.1 JavaScript 调用栈大小的限制
如果忘记加上用以停止函数递归调用的边界条件,会发生什么呢?递归并不会无限地执行下
去;浏览器会抛出错误,也就是所谓的栈溢出错误(stack overflow error)。
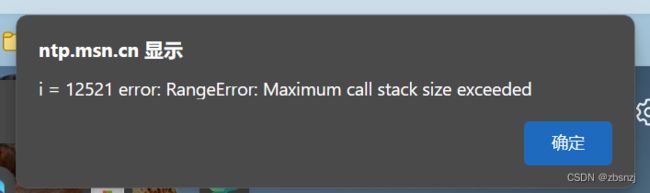
每个浏览器都有自己的上限,可用以下代码测试:
var i=0
function recursiveFn(){
i++
recursiveFn()
}
try{
recursiveFn()
}catch(ex){
alert('i = '+i+' error: '+ex)
}ECMAScript 6有尾调用优化(tail call optimization)。如果函数内最后一个操作是调用函数(就像示例中加粗的那行),会通过“跳转指令”(jump) 而不是“子程序调用”(subroutine call)来控制。也就是说,在ECMAScript 6中,这里的代码可以一直执行下去。所以,具有停止递归的边界条件非常重要。
10.1.2 斐波那契数列
斐波那契数列的定义如下:
1和2的斐波那契数是 1;
n(n>2)的斐波那契数是(n1)的斐波那契数加上(n2)的斐波那契数。
那么,让我们开始实现斐波那契函数:
function fibonacci(num){
if(num ===1 || num ===2){
return 1
}
return fibonacci(num-1)+fibonacci(num-2)
}我们已经知道,当n大于2时,Fibonacci(n)等于Fibonacci(n1)+Fibonacci(n2)。
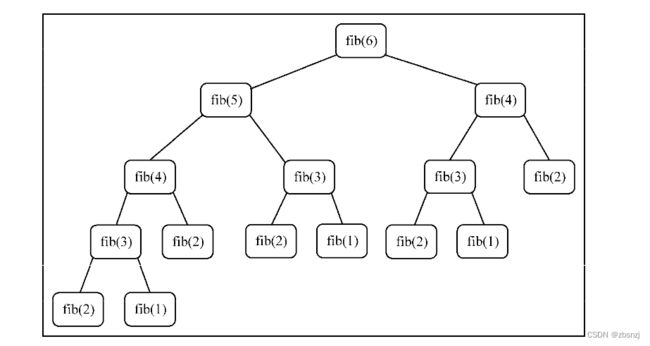
现在,斐波那契函数实现完毕。让我们试着找出6的斐波那契数,其会产生如下函数调用:
我们也可以用非递归的方式实现斐波那契函数:
function fib(num){
var n1 = 1,
n2 = 1,
n = 1;
for (var i = 3; i<=num; i++){
n = n1 + n2;
n1 = n2;
n2 = n;
}
return n;
}为何用递归呢?更快吗?递归并不比普通版本更快,反倒更慢。但要知道,递归更容易理解,并且它所需的代码量更少。
10.2 动态规划
动态规划(Dynamic Programming,DP)是一种将复杂问题分解成更小的子问题来解决的优
化技术。
用动态规划解决问题时,要遵循三个重要步骤:
(1) 定义子问题;
(2) 实现要反复执行来解决子问题的部分(这一步要参考前一节讨论的递归的步骤);
(3) 识别并求解出边界条件。
10.2.1 最少硬币找零问题
最少硬币找零问题是硬币找零问题的一个变种。硬币找零问题是给出要找零的钱数,以及可
用的硬币面额d1…d n及其数量,找出有多少种找零方法。最少硬币找零问题是给出要找零的钱数,以及可用的硬币面额d1…d n及其数量,找到所需的最少的硬币个数。
例如,美国有以下面额(硬币):d1=1,d2=5,d3=10,d4=25。
如果要找36美分的零钱,我们可以用1个25美分、1个10美分和1个便士(1美分)。
如何将这个解答转化成算法?
最少硬币找零的解决方案是找到n所需的最小硬币数。但要做到这一点,首先得找到对每个
x
function MinCoinChange(coins){
var coins = coins; //{1}
var cache = {}; //{2}
this.makeChange = function(amount) {
var me = this;
if (!amount) { //{3}
return [];
}
if (cache[amount]) { //{4}
return cache[amount];
}
var min = [], newMin, newAmount;
for (var i=0; i= 0){
newMin = me.makeChange(newAmount); //{7}
}
if (newAmount >= 0 && //{8}
(newMin.length < min.length-1 || !min.length)//{9}
&& (newMin.length || !newAmount)) //{10})
{
min = [coin].concat(newMin); //{11}
console.log('new Min ' + min + ' for ' + amount);
}
}
return (cache[amount] = min); //{12}
}
} 为了更有条理,我们创建了一个类,解决给定面额的最少硬币找零问题。让我们一步步解读
这个算法。
MinCoinChange类接收coins参数(行{1}),该参数代表问题中的面额。对美国的硬币系
统而言,它是[1, 5, 10, 25]。我们可以随心所欲传递任何面额。此外,为了更加高效且不重
复计算值,我们使用了cache(行{2})。
接下来是makeChange方法,它也是一个递归函数,找零问题由它解决。首先,若amount
不为正(< 0),就返回空数组(行{3});方法执行结束后,会返回一个数组,包含用来找零的各
个面额的硬币数量(最少硬币数)。接着,检查cache缓存。若结果已缓存(行{4}),则直接返
回结果;否则,执行算法。
我们基于coins参数(面额)解决问题。因此,对每个面额(行{5}),我们都计算newAmount
(行{6})的值,它的值会一直减小,直到能找零的最小钱数(别忘了本算法对所有的x < amount
都会计算makeChange结果)。若newAmount是合理的值(正值),我们也会计算它的找零结果(行{7})。
最后,我们判断newAmount是否有效,minValue (最少硬币数)是否是最优解,与此同时
minValue和newAmount是否是合理的值({行10})。若以上判断都成立,意味着有一个比之前
更优的答案(行{11}。以5美分为例,可以给5便士或者1个5美分镍币,1个5美分镍币是最优解)。
最后,返回最终结果(行{12})。
测试一下这个算法:
10.2.2 背包问题
背包问题是一个组合优化问题。它可以描述如下:给定一个固定大小、能够携重W的背包,
以及一组有价值和重量的物品,找出一个最佳解决方案,使得装入背包的物品总重量不超过W,
且总价值最大。
下面是一个例子:
考虑背包能够携带的重量只有5。对于这个例子,我们可以说最佳解决方案是往背包里装入
物品1和物品2,这样,总重量为5,总价值为7。
我们来看看下面这个背包算法:
function knapSack(capacity, weights, values, n) {
var i, w, a, b, kS = [];
for (i = 0; i <= n; i++) { //{1}
kS[i] = [];
}
for (i = 0; i <= n; i++) {
for (w = 0; w <= capacity; w++) {
if (i == 0 || w == 0) { //{2}
kS[i][w] = 0;
} else if (weights[i-1] <= w) { //{3}
a = values[i-1] + kS[i-1][w-weights[i-1]];
b = kS[i-1][w];
kS[i][w] = (a > b) ? a : b; //{4} max(a,b)
} else {
kS[i][w] = kS[i-1][w]; //{5}
}
}
}
return kS[n][capacity]; //{6}
} 我们来看看这个算法是如何工作的。
行{1}:首先,初始化将用于寻找解决方案的矩阵ks[n+1][capacity+1]。
行{2}:忽略矩阵的第一列和第一行,只处理索引不为0的列和行。
行{3}:物品i的重量必须小于约束(capacity)才有可能成为解决方案的一部分;否则,总重量就会超出背包能够携带的重量,这是不可能发生的。发生这种情况时,只要忽略它,用之前的值就可以了(行{5})。
行{4}:当找到可以构成解决方案的物品时,选择价值最大的那个。
行{6}:最后,问题的解决方案就在这个二维表格右下角的最后一个格子里。
我们可以用开头的例子来测试这个算法:
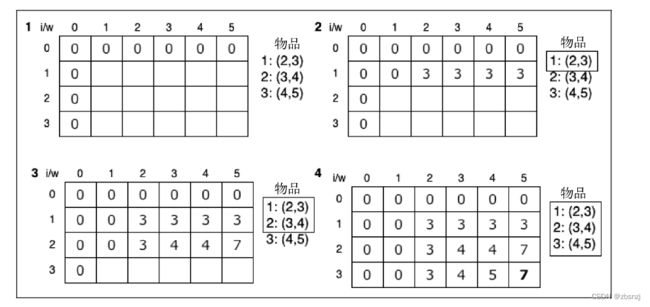
下图举例说明了例子中kS矩阵的构造:
请注意,这个算法只输出背包携带物品价值的最大值,而不列出实际的物品。我们可以增加
下面的附加函数来找出构成解决方案的物品:
function findValues(n, capacity, kS, weights, values) {
var i = n, k = capacity;
console.log('解决方案包含以下物品:');
while (i > 0 && k > 0) {
if (kS[i][k] !== kS[i-1][k]) {
console.log('物品' + i + ',重量:' + weights[i-1] + ',价值:' + values[i-1]);
i--;
k = k - kS[i][k];
} else {
i--;
}
}
}10.2.3 最长公共子序列
另一个经常被当作编程挑战问题的动态规划问题是最长公共子序列(LCS):找出两个字符
串序列的最长子序列的长度。最长子序列是指,在两个字符串序列中以相同顺序出现,但不要求
连续(非字符串子串)的字符串序列。
考虑如下例子:
function lcs(wordX, wordY) {
var m = wordX.length,
n = wordY.length,
l = [],
solution=[],
i, j, a, b;
for (i = 0; i <= m; ++i) {
l[i] = [];
solution[i] = []//{1}
for (j = 0; j <= n; ++j) {
l[i][j] = 0;
solution[i][j] = '0'//{2}
}
}
for (i = 0; i <= m; i++) {
for (j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
l[i][j] = 0;
} else if (wordX[i-1] == wordY[j-1]) {
l[i][j] = l[i-1][j-1] + 1;
solution[i][j] = 'diagonal'//{3}
} else {
a = l[i-1][j];
b = l[i][j-1];
l[i][j] = (a > b) ? a : b; //max(a, b)
solution[i][j]=(l[i][j] == l[i-1][j]) ? 'top' : 'left'//{4}
}
}
}
printSolution(solution, l, wordX, wordY, m, n)//{5}
return l[m][n];
}
function printSolution(solution, l, wordX, wordY, m, n) {
var a = m, b = n, i, j,
x = solution[a][b],
answer = '';
while (x !== '0') {
if (solution[a][b] === 'diagonal') {
answer = wordX[a - 1] + answer;
a--;
b--;
} else if (solution[a][b] === 'left') {
b--;
} else if (solution[a][b] === 'top') {
a--;
}
x = solution[a][b];
}
console.log('lcs: '+ answer);
} 比较背包问题和LCS算法,我们会发现两者非常相似。这项从顶部开始构建解决方案的技术
被称为记忆,而解决方案就在表格或矩阵的右下角。
10.2.4 矩阵链相乘
矩阵链相乘是另一个可以用动态规划解决的著名问题。这个问题是要找出一组矩阵相乘的最
佳方式(顺序)。
让我们试着更好地理解这个问题。n行m列的矩阵A和m行p列的矩阵B相乘,结果是n行p列的
矩阵C。
考虑我们想做A*B*C*D的乘法。因为乘法满足结合律,所以我们可以让这些矩阵以任意顺
序相乘。因此,考虑如下情况:
A是一个10行100列的矩阵
B是一个100行5列的矩阵
C是一个5行50列的矩阵
D是一个50行1列的矩阵
A*B*C*D的结果是一个10行1列的矩阵
在这个例子里,相乘的方式有五种。
(1) (A(B(CD))):乘法运算的次数是1750次。
(2) ((AB)(CD)):乘法运算的次数是5300次。
(3) (((AB)C)D):乘法运算的次数是8000次。
(4) ((A(BC))D):乘法运算的次数是75 500次。
(5) (A((BC)D)):乘法运算的次数是31 000次。
相乘的顺序不一样,要进行的乘法运算总数也有很大差异。那么,要如何构建一个算法,求
出最少的乘法运算操作次数?矩阵链相乘的算法如下:
function matrixChainOrder(p, n) {
var i, j, k, l, q, m = [];
var s = [];
for (i = 0; i <= n; i++) {
s[i] = [];
for (j = 0; j <= n; j++) {
s[i][j] = 0;
}
}
for (i = 1; i <= n; i++) {
m[i] = [];
m[i][i] = 0;
}
for (l = 2; l < n; l++) {
for (i = 1; i <= n-l+1; i++) {
j = i+l-1;
m[i][j] = Number.MAX_SAFE_INTEGER;
for (k = i; k <= j-1; k++) {
q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j]; //{1}
if (q < m[i][j]){
m[i][j] = q;
s[i][j] = k//{2}
}
}
}
}
printOptimalParenthesis(s, 1, n-1)//{3}
return m[1][n-1];
}
function printOptimalParenthesis(s, i, j) {
if (i == j) {
console.log("A[" + i + "]");
} else {
console.log("(");
printOptimalParenthesis(s, i, s[i][j]);
printOptimalParenthesis(s, s[i][j] + 1, j);
console.log(")");
}
} 执行修改后的算法,也能得到括号的最佳顺序(A[1](A[2](A[3]A[4]))),并可以转化为
(A(B(CD)))。
10.3 贪心算法
贪心算法遵循一种近似解决问题的技术,期盼通过每个阶段的局部最优选择(当前最好的
解),从而达到全局的最优(全局最优解)。它不像动态规划算法那样计算更大的格局。
10.3.1 最少硬币找零
最少硬币找零问题也能用贪心算法解决。大部分情况下的结果是最优的,不过对有些面额而
言,结果不会是最优的。
function MinCoinChange(coins){
var coins = coins //{1}
this.makeChange = function(amount) {
var change = [],
total = 0
for (var i=coins.length; i>=0; i--){ //{2}
var coin = coins[i]
while (total + coin <= amount) { //{3}
change.push(coin) //{4}
total += coin //{5}
}
}
return change;
}
} 不得不说贪心版本的MinCoinChange比动态规划版本的简单多了。和动态规划方法相似,
我们传递面额参数,实例化MinCoinChange(行{1})。
对每个面额(行{2}——从大到小),把它的值和total相加后,total需要小于amount(行
{3})。我们会将当前面额coin添加到结果中(行{4}),也会将它和total相加(行{5})。
如你所见,这个解法很简单。从最大面额的硬币开始,拿尽可能多的这种硬币找零。当无法
再拿更多这种价值的硬币时,开始拿第二大价值的硬币,依次继续。
用和DP方法同样的测试代码测试:
var minCoinChange = new MinCoinChange([1, 5, 10, 25])
console.log(minCoinChange.makeChange(36))
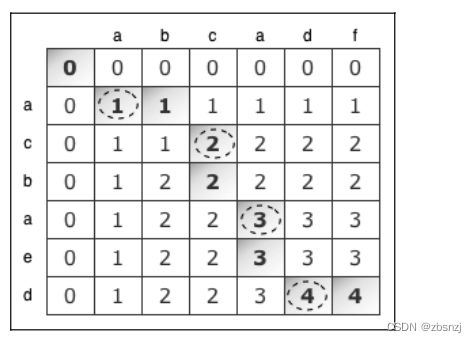
结果依然是[25, 10, 1],和用DP得到的一样。下图阐释了算法的执行过程:
然而,如果用[1, 3, 4]面额执行贪心算法,会得到结果[4, 1, 1]。如果用动态规划的解法,会得到最优的结果[3, 3]。
比起动态规划算法而言,贪心算法更简单、更快。然而,如我们所见,它并不总是得到最优答案。但是综合来看,它相对执行时间来说,输出了一个可以接受的解。
10.3.2 分数背包问题
求解分数背包问题的算法与动态规划版本稍有不同。在0-1背包问题中,只能向背包里装入
完整的物品,而在分数背包问题中,我们可以装入分数的物品。我们用前面用过的例子来比较两
者的差异,如下所示:
在动态规划的例子里,我们考虑背包能够携带的重量只有5。而在这个例子里,我们可以说
最佳解决方案是往背包里装入物品1和物品2,总重量为5,总价值为7。
如果在分数背包问题中考虑相同的容量,得到的结果是一样的。因此,我们考虑容量为6的
情况。
在这种情况下,解决方案是装入物品1和物品2,还有25%的物品3。这样,重量为6的物品总
价值为8.25。
我们来看看下面这个算法:
function knapSack(capacity, values, weights) {
var n = values.length,
load = 0, i = 0, val = 0
for (i = 0; i < n && load < capacity; i++) { //{1}
if (weights[i] <= (capacity - load)) { //{2}
val += values[i]
load += weights[i]
} else {
var r = (capacity - load) / weights[i] //{3}
val += r * values[i]
load += weights[i]
}
}
return w
} 行{1}:总重量少于背包容量,继续迭代,装入物品。
行{2}:如果物品可以完整地装入背包,就将其价值和重量分别计入背包已装入物品的总
价值(val)和总重量(load)。
行{3}:如果物品不能完整地装入背包,计算能够装入部分的比例(r)。
如果在0-1背包问题中考虑同样的容量6,我们就会看到,物品1和物品3组成了解决方案。在
这种情况下,对同一个问题应用不同的解决方法,会得到两种不同的结果。