pybind11:对比C++和Python解线性方程组的速度
前言
上篇博客介绍了如何在用pybind11实现ndarray和C++数组的转换自由,pybind11:实现ndarray转C++原生数组(没看过的朋友可以去看一看)下面我们以一个实际的算法例子演示一下如何使用这个技术,方便的实现 Python 调用 C++ 写的算法,并观察两个语言分别运行同一算法时,算法速率的显著性差异。
算法选择
解线性方程组在工程乃至很多领域都是一项非常重要的技术,该算法的时间复杂度也是人们一直在追求的。下面就以手写最经典的 Gauss列主元素消去法 来作为实例算法演示C++和Python的运行速率的差距。
它的算法先后对比较简单,主要分为消去和回代两个过程,消去即通过矩阵行变换将一个普通的矩阵(增广矩阵)转化为一个上三角矩阵,回代即从主对角线上最后一个元素( x n x_n xn)开始往回代,依次计算出( x n x_n xn, x n − 1 x_{n-1} xn−1, … , x 1 x_1 x1)的值,具体过程如下
C++
#include Python
import numpy as np
# A: 系数矩阵 b: 右侧常数向量
# 即计算 Ax = b
def solve(A, d):
# 确保以浮点型数据计算
A.astype(np.float64)
d.astype(np.float64)
a = np.hstack((A, d.reshape(len(d), 1))) # 水平拼接(先将d转化为列向量)
n = len(A[0])
for k in range(n - 1):
# 选主元
for p in range(k+1, n):
if np.abs(a[p, k]) == np.max(np.abs(a[k:, k])):
a[k, :], a[p, :] = a[p, :], a[k, :].copy()
# 消元
for i in range(k+1, n):
a[i, k:] = a[i, k:] - a[i, k] / a[k, k] * a[k, k:]
# 回代
x = np.zeros(n)
x[n-1] = a[n-1, n] / a[n-1, n-1]
for i in range(n-2, -1, -1):
x[i] = (a[i, n] - np.sum(a[i, i+1:n] * x[i+1:])) / a[i, i]
return x
不难看出,C++代码远比Python代码复杂,单从使用的循环数量粗糙的分析,C++代码中使用了两个二重循环(水平拼接和选主元)和两个三重循环(消元和回代)而Python代码只用到了两个二重循环(选主元和消元)和一个一重循环(消元和回代),所以无论是算法的时间复杂度还是空间复杂度,Python代码都远小于C++的,那么它们实际的运行速度的快慢呢?
构建项目
构建项目,使用Pybind11将C++代码编译为pyd文件,项目结构即配置过程的详情参考:pybind11:实现Python调用C++代码(入门)
核心cpp代码如下:
#include “pybind11_tools.cpp” 中装有自主编写的实现ndarray和C++数组相互转化的API(InputMatrix, InputVector, CToNdarray),代码详情参考:pybind11:实现ndarray转C++原生数组
调用写好的接口可以很方便的将写好的C++代码打包为二进制文件(pyd文件)提供给Python使用。将生成的pyd文件(tryPybind)放置于测试代码一个目录下,即可开始测试
开始测试
首先测试是否正常(以numpy的(linalg.solve函数))计算的结果为标准答案)
import numpy as np
import python_tool as pytool
import tryPybind # 编译好的C++二进制文件
# ax = b (随便定义一个方程组)
a = np.array([[1., 5., 3.],
[4., 2., 6.],
[9., 8., 7.]])
b = np.array([10., 20. ,30.])
print('python运算结果:')
x1 = pytool.solve(a, b)
print(x1)
print('C++运算结果:')
x2 = tryPybind.solve(a, b)
print(x2)
print('numpy运算结果:')
x3 = np.linalg.solve(a, b)
print(x3)
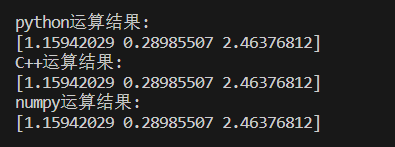
结果如下:
算法没大问题,接下来测试对比运行时间,用rand生成一组随机的1000维线性方程组,分别计算运行时间,代码如下:
import numpy as np
import python_tool as pytool
import time
import tryPybind
# ax = b (1000维)
a = np.random.rand(1000, 1000)
b = np.random.rand(1000)
print('计算一个1000维的线性方程组,分别耗时如下:')
t1 = time.time()
x1 = pytool.solve(a, b)
t2 = time.time()
print("Python耗时: " + str(t2 - t1) + '秒')
t1 = time.time()
x2 = tryPybind.solve(a, b)
t2 = time.time()
print("C++耗时: " + str(t2 - t1) + '秒')
t1 = time.time()
x3 = np.linalg.solve(a, b)
t2 = time.time()
print('numpy耗时: ' + str(t2 - t1) + '秒')
多次执行该代码,结果如下:
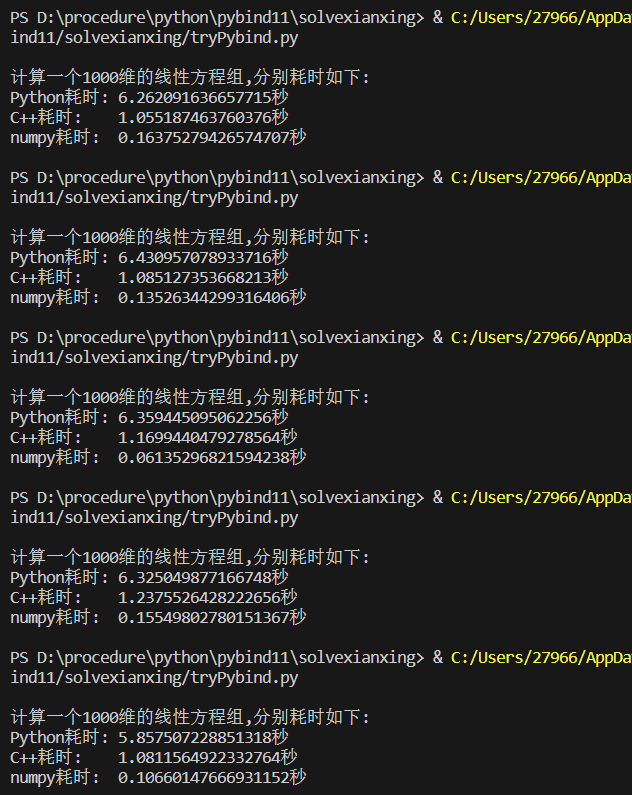
不难发现,Python代码虽然算法简介,复杂度低,但实际的运算速率远慢于低于C++(接近6倍),以此可直观的看见解释性语言的效率之慢的通病,更能体现出在Python代码中调用写好的C++代码所带来的强大优势。同时也可发现numpy每次都能以不到 0.2 秒的速度算完了一个1000维的线性方程组,其算法之强大。