＜二叉树（链式）＞《数据结构(C语言版)》
目录
《数据结构(C语言版)》之二叉树（链式）实现
——By 作者：新晓·故知
一、二叉树（链式）
二叉树（链式）实现的重要思想：
问题思考：
1.二叉树的创建
2.二叉树的遍历
2.1 前序、中序以及后序遍历
2.2 层序遍历
2.3 节点个数以及高度等
二、二叉树（链式）实现分析：
二叉树（链式）实现测试实例：
（1）定义二叉树链式结构
思路：孩子兄弟表示法——存储树的最优结构
（2）创建链式二叉树--手动创建的是已知二叉树的结构
（3）动态开辟新结点
(4）前序遍历（先序遍历）
前序遍历 （先序遍历）：双路递归调用分析
（5）中序遍历
中序遍历 ：双路递归调用分析
（6）后序遍历
后序遍历 ：双路递归调用分析
（7）打印二叉树的结点的个数
①写法1：count定义成局部变量
②写法2：count定义成静态局部变量
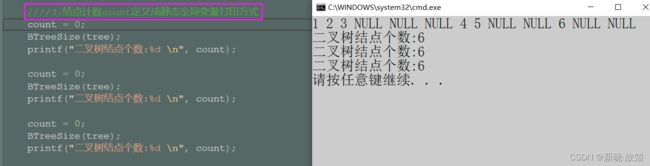
③写法3：count定义成全局变量
④写法4：count定义成静态全局变量
⑤写法5：count既不定义成局部变量，也不定义成全局变量（思想：遍历+计数）
⑥写法6：count既不定义成局部变量，也不定义成全局变量（分治思想）
分治：
对于二叉树的分治：
（8）打印二叉树叶子结点的个数
（9）打印二叉树第k层的结点的个数
思路：利用分治
（10）打印二叉树的深度
思路：利用分治
调试测试：
（11）打印二叉树查找值x的结点
思路：
（12）销毁二叉树
思路：借助后序遍历进行销毁
调试测试：
（13）层序遍历
思路：借助队列
对于本例二叉树：
这里需要附用之前队列的功能实现的代码！
队列实现代码链接：
＜队列（链式）＞《数据结构(C语言版)》
代码接口注意：
（14）判断二叉树是否为完全二叉树
思路：借助层序遍历。
三、二叉树（链式）实现完整源码
完整源码如下，欢迎复制测试指正！
BTreeChain.c :
附用队列实现源码：
Queue.h：
Queue.c：
后记：●由于作者水平有限，文章难免存在谬误之处，敬请读者斧正，俚语成篇，恳望指教！
——By 作者：新晓·故知
《数据结构(C语言版)》之二叉树（链式）实现
——By 作者：新晓·故知
一、二叉树（链式）
二叉树（链式）实现的重要思想：
1.递归是一种非常重要的思想，而在二叉树（链式）的实现中，递归更是体现的淋漓尽致。尤其是在进行二叉树的遍历中，更是使用了双路递归！这使得二叉树（链式）的实现更加方便。
（三路递归应用在二叉树的三叉链结构中，递归过程更为复杂，但递归过程思想同双路递归一样。）
2.分治也是一种非常重要的思想，在二叉树（链式）的实现中，多处用到了分治（即“分而治之”）。
问题思考：
在以往的学习中，实现了各种结构的增、删、查、改等功能。对于二叉树，普通的二叉树增删查改实际应用价值很小，如果是为了单纯存储数据，不如使用线性表。
此处学习链式二叉树，是为了学习它的结构，掌握控制方法，为了后序学习更复杂的搜索二叉树等做铺垫。
1.二叉树的创建
在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入，为了降低大家学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，我们反过头再来研究二叉树真正的创建方式。
此处手动创建二叉树：
二叉树基本操作前，再 回顾下二叉树的概念， 二叉树是：
1. 空树2. 非空：根节点，根节点的左子树、根节点的右子树组成的
从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的。
2.二叉树的遍历
2.1 前序、中序以及后序遍历
学习二叉树结构，最简单的方式就是遍历。所谓 二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。
按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：
1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根， 所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。
NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
// 二叉树前序遍历void PreOrder(BTNode* root);// 二叉树中序遍历void InOrder(BTNode* root);// 二叉树后序遍历void PostOrder(BTNode* root);
下面主要分析前序递归遍历，中序与后序图解类似。
前序遍历递归图解：
前序遍历结果： 1 2 3 4 5 6中序遍历结果： 3 2 1 5 4 6后序遍历结果： 3 1 5 6 4 1
前序遍历示例：
中序遍历示例：
后序遍历示例：
层序遍历示例：
2.2 层序遍历
层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。
// 层序遍历void LevelOrder(BTNode* root);
2.3 节点个数以及高度等
// 二叉树节点个数int BinaryTreeSize(BTNode* root);// 二叉树叶子节点个数int BinaryTreeLeafSize(BTNode* root);// 二叉树第k层节点个数int BinaryTreeLevelKSize(BTNode* root, int k);// 二叉树查找值为x的节点BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
二、二叉树（链式）实现分析：
二叉树（链式）实现测试实例：
（1）定义二叉树链式结构
思路：孩子兄弟表示法——存储树的最优结构
链接：＜二叉树＞《数据结构(C语言版)》
https://blog.csdn.net/m0_57859086/article/details/123922185?spm=1001.2014.3001.5502
//定义二叉树链式结构 typedef int BTDataType; typedef struct BinaryTreeNode { struct BinaryTreeNode* left; struct BinaryTreeNode* right; BTDataType data; }BTNode;（2）创建链式二叉树--手动创建的是已知二叉树的结构
示例：
//创建链式二叉树--创建的是已知二叉树的结构 BTNode* CreatBinaryTree() { BTNode* node1 = BuyBTNode(1); BTNode* node2 = BuyBTNode(2); BTNode* node3 = BuyBTNode(3); BTNode* node4 = BuyBTNode(4); BTNode* node5 = BuyBTNode(5); BTNode* node6 = BuyBTNode(6); node1->left = node2; node1->right = node4; node2->left = node3; node4->left = node5; node4->right = node6; return node1; }
（3）动态开辟新结点
//动态开辟新结点 BTNode* BuyBTNode(BTDataType x) { BTNode* node = (BTNode*)malloc(sizeof(BTNode)); if (node == NULL) { printf("malloc fail\n"); exit(-1); } //初始化新结点 node->data = x; node->left = node->right = NULL; return node; }(4）前序遍历（先序遍历）
//前序遍历（先序遍历） void PreOrder(BTNode* root) { if (root == NULL) { printf("NULL "); return; } printf("%d ", root->data); PreOrder(root->left); PreOrder(root->right); }
前序遍历 （先序遍历）：双路递归调用分析
（5）中序遍历
//中序遍历 void InOrder(BTNode* root) { if (root == NULL) { printf("NULL "); return; } InOrder(root->left); printf("%d ", root->data); InOrder(root->right); }中序遍历 ：双路递归调用分析
（6）后序遍历
//后序遍历 void PostOrder(BTNode* root) { if (root == NULL) { printf("NULL "); return; } PostOrder(root->left); PostOrder(root->right); printf("%d ", root->data); }
后序遍历 ：双路递归调用分析
（7）打印二叉树的结点的个数
①写法1：count定义成局部变量
//一、打印二叉树的结点的个数 //写法1：count定义成局部变量，这样写，相当于每个栈帧都有一个count，重复计数，不可取！！！ //这是在递归，无法加到一个count // (以前序打印为例） void BTreeSize(BTNode* root) { int count = 0; if (root == NULL) return ; ++count; BTreeSize(root->left); BTreeSize(root->right); }②写法2：count定义成静态局部变量
注：
定义成局部变量，想要拿到，必须添加返回值语句，但无法再初始化！
而定义成全局变量，可以直接拿到，无需添加返回值语句 。
//写法2：count定义成静态局部变量，但需要返回值,其类型为int //多次打印会出错，累加打印，不可取 // 定义成局部变量，想要拿到，必须添加返回值语句， // 定义成全局变量，可以直接拿到，无需添加返回值语句 //(前序打印） int BTreeSize(BTNode* root) { static int count = 0; if (root == NULL) return count; ++count; BTreeSize(root->left); BTreeSize(root->right); return count; }③写法3：count定义成全局变量
//写法3：count定义成全局变量（可以打印） //全局变量存储在静态区，而非栈帧，遍历时，当遇到空结点就返回，当不为空，就++ //1.打印二叉树的结点的个数(前序打印） int count = 0; void BTreeSize(BTNode* root) { if (root == NULL) return; ++count; BTreeSize(root->left); BTreeSize(root->right); }//2.打印二叉树的结点的个数(中序打印） int count = 0; void BTreeSize(BTNode* root) { if (root == NULL) return; BTreeSize(root->left); ++count; BTreeSize(root->right); }//3.打印二叉树的结点的个数(后序打印） int count = 0; void BTreeSize(BTNode* root) { if (root == NULL) return; BTreeSize(root->left); BTreeSize(root->right); ++count; }④写法4：count定义成静态全局变量
//总结：以上定义成局部变量，静态局部变量都不够好！ //1.count定义成静态局部变量，每次调用无法初始化为0，当多次打印会出现累加计数 //因此count应采用全局变量或者定义成静态全局变量 //2.count定义成全局变量，会涉及到线程安全问题，这涉及到Linux的内容 //写法4：将count定义成静态全局变量（可以打印） static int count = 0; int BTreeSize(BTNode* root) { if (root == NULL) return count; BTreeSize(root->left); BTreeSize(root->right); ++count; return count; }⑤写法5：count既不定义成局部变量，也不定义成全局变量（思想：遍历+计数）
//写法5：count既不定义成局部变量，也不定义成全局变量 //思想：遍历+计数 //将一个变量的地址传过去, //前序计数打印为例 void BTreeSize(BTNode* root, int* pCount) { if (root == NULL) return; ++(*pCount); BTreeSize(root->left, pCount); BTreeSize(root->right, pCount); }⑥写法6：count既不定义成局部变量，也不定义成全局变量（分治思想）
//写法6：count既不定义成局部变量，也不定义成全局变量 //分治思想 //前序计数打印为例 int BTreeSize(BTNode* root) { return root == NULL ? 0 : BTreeSize(root->left) + BTreeSize(root->right) + 1; }
分治：
将复杂的问题，分成更小规模的子问题，子问题再分成更小规模的子问题.......直到子问题不可再分割，直接能得出结果。
对于二叉树的分治：
1.判断是否为空树。当为空树，结点返回为0。
2.非空树。将左子树结点个数+右子树结点个数+1（根结点）
（8）打印二叉树叶子结点的个数
//二、打印二叉树叶子结点的个数 //思路1：遍历+计数 //思路2：分治思想 //分治实现 int BTreeLeafSize(BTNode* root) { if (root == NULL) return 0; if (root->left == NULL && root->right == NULL) return 1; return BTreeLeafSize(root->left) + BTreeLeafSize(root->right); }（9）打印二叉树第k层的结点的个数
思路：利用分治
1.当为空树时，返回0
2.非空树，且层数k==1，返回1
3.非空树，且层数k>1,转换成：左子树k-1层结点个数+右子树k-1层结点个数。
//三、打印二叉树第k层的结点的个数 int BTreeKLevelSize(BTNode* root, int k) { assert(k >= 1); if (root == NULL) return 0; if (k == 1) return 1; return BTreeKLevelSize(root->left, k - 1) + BTreeKLevelSize(root->right, k - 1); }（10）打印二叉树的深度
思路：利用分治
左子树的高度与右子树的高度相比较，大的那个就加1
//四、打印二叉树的深度（高度） int BTreeDepth(BTNode* root) { if (root == NULL) return 0; int leftDepth = BTreeDepth(root->left); int rightDepth = BTreeDepth(root->right); return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1; }调试测试：
（11）打印二叉树查找值x的结点
思路：
对二叉树进行遍历，找到了就返回调用处，层层返回，直至首次调用，而不是直接返回打印！
//五、二叉树查找值x的结点 //找到了就返回调用处，层层返回，直至首次调用，而不是直接返回打印！ BTNode* BTreeFind(BTNode* root, BTDataType x) { //树形结构实现查找 //以前序遍历为例 if (root == NULL) return NULL; if (root->data == x) return root; //写法1： //BTNode* ret1 = BTreeFind(root->left, x); //if (ret1) // return ret1; //BTNode* ret2 = BTreeFind(root->right, x); //if (ret2) // return ret2; 写法2：使用三目运算符 return (BTreeFind(root->left, x))? BTreeFind(root->left, x):BTreeFind(root->right, x); //或者 //return (BTreeFind(root->right, x)) ? BTreeFind(root->right, x) : BTreeFind(root->left, x); //写法3： //BTNode* ret1 = BTreeFind(root->left, x); //if (ret1) // return ret1; //return (BTreeFind(root->right, x)); /*//虽然可以正确打印，但这样就破坏了二叉树的遍历顺序 不可取 BTNode* ret2 = BTreeFind(root->right, x); if (ret2) return ret2; return (BTreeFind(root->left, x));*/ return NULL; }（12）销毁二叉树
思路：借助后序遍历进行销毁
调试测试：
//六、二叉树的销毁 //思想：后序遍历进行销毁 //传一级指针无需置空，置空无用 //传二级指针需要置空 void BTreeDestroy(BTNode* root) { if (root == NULL) return; BTreeDestroy(root->left); BTreeDestroy(root->right); free(root); //root = NULL; //传一级指针置空不起作用 }（13）层序遍历
思路：借助队列
先将根结点入队，根据队列先进先出的性质。当上一层的结点出队的时候，把下一层的结点入队......
对于本例二叉树：
先将根1入队，当1出队，将2、4入队，2出队，将3入队（其实包括3和NULL，而NULL不入队列），4出队，5、6入队......
七、层序遍历 借助队列 void LevelOrder(BTNode* root) { Queue q; QueueInit(&q); if (root) { QueuePush(&q, root); } while (!QueueEmpty(&q)) { BTNode* front = QueueFront(&q); QueuePop(&q); printf("%d ", front->data); if (front->left) QueuePush(&q, front->left); if (front->right) QueuePush(&q, front->right); } printf("\n"); QueueDestroy(&q); }这里需要附用之前队列的功能实现的代码！
队列实现代码链接：
＜队列（链式）＞《数据结构(C语言版)》
代码接口注意：
（14）判断二叉树是否为完全二叉树
思路：借助层序遍历。
首先将根结点入队，空结点也入队，当有空结点出队以后，不再入队任何结点，将队列中所有结点出队，如果全是空，就是完全二叉树，如果有非空结点，就不是完全二叉树。
//八、判断二叉树是否为完全二叉树 //bool值类型 //return false<==>0<==>假 //return true<==>1<==>真 bool BTreeComplete(BTNode* root) { Queue q; QueueInit(&q); if (root) { QueuePush(&q, root); } while (!QueueEmpty(&q)) { BTNode* front = QueueFront(&q); QueuePop(&q); if (front == NULL) break; QueuePush(&q, front->left); QueuePush(&q, front->right); } while (!QueueEmpty(&q)) { BTNode* front = QueueFront(&q); QueuePop(&q); //遍历到空值，若后面又遍历到非空，那么说明不是完全二叉树 if (front) { //判断后需要销毁队列，否则就会造成内存泄漏 QueueDestroy(&q); printf("此二叉树不是完全二叉树\n"); return false; } } //判断后需要销毁队列，否则就会造成内存泄漏 QueueDestroy(&q); printf("此二叉树是完全二叉树\n"); return true; }
三、二叉树（链式）实现完整源码
完整源码如下，欢迎复制测试指正！
BTreeChain.c :
#include#include #include #include"Queue.h" #include //定义二叉树链式结构 typedef int BTDataType; typedef struct BinaryTreeNode { struct BinaryTreeNode* left; struct BinaryTreeNode* right; BTDataType data; }BTNode; //动态开辟新结点 BTNode* BuyBTNode(BTDataType x) { BTNode* node = (BTNode*)malloc(sizeof(BTNode)); if (node == NULL) { printf("malloc fail\n"); exit(-1); } //初始化新结点 node->data = x; node->left = node->right = NULL; return node; } //创建链式二叉树--创建的是已知二叉树的结构 BTNode* CreatBinaryTree() { BTNode* node1 = BuyBTNode(1); BTNode* node2 = BuyBTNode(2); BTNode* node3 = BuyBTNode(3); BTNode* node4 = BuyBTNode(4); BTNode* node5 = BuyBTNode(5); BTNode* node6 = BuyBTNode(6); //BTNode* node7 = BuyBTNode(7); //新增此语句，用来测试判断是否为完全二叉树 node1->left = node2; node1->right = node4; node2->left = node3; //node2->right = node7; //新增此语句，用来测试判断是否为完全二叉树 node4->left = node5; node4->right = node6; return node1; } //前序遍历（先序遍历） void PreOrder(BTNode* root) { if (root == NULL) { printf("NULL "); return; } printf("%d ", root->data); PreOrder(root->left); PreOrder(root->right); } //中序遍历 void InOrder(BTNode* root) { if (root == NULL) { printf("NULL "); return; } InOrder(root->left); printf("%d ", root->data); InOrder(root->right); } //后序遍历 void PostOrder(BTNode* root) { if (root == NULL) { printf("NULL "); return; } PostOrder(root->left); PostOrder(root->right); printf("%d ", root->data); } 一、打印二叉树的结点的个数 写法1：count定义成局部变量，这样写，相当于每个栈帧都有一个count，重复计数，不可取！！！ 这是在递归，无法加到一个count (以前序打印为例） //void BTreeSize(BTNode* root) //{ // int count = 0; // if (root == NULL) // return ; // ++count; // BTreeSize(root->left); // BTreeSize(root->right); //} 写法2：count定义成静态局部变量，但需要返回值,其类型为int 多次打印会出错，累加打印，不可取 定义成局部变量，想要拿到，必须添加返回值语句， 定义成全局变量，可以直接拿到，无需添加返回值语句 (前序打印） //int BTreeSize(BTNode* root) //{ // static int count = 0; // if (root == NULL) // return count; // ++count; // BTreeSize(root->left); // BTreeSize(root->right); // // return count; //} //写法3：count定义成全局变量（可以打印） //全局变量存储在静态区，而非栈帧，遍历时，当遇到空结点就返回，当不为空，就++ //1.打印二叉树的结点的个数(前序打印） //int count = 0; //void BTreeSize(BTNode* root) //{ // if (root == NULL) // return; // ++count; // BTreeSize(root->left); // BTreeSize(root->right); //} 2.打印二叉树的结点的个数(中序打印） //int count = 0; //void BTreeSize(BTNode* root) //{ // if (root == NULL) // return; // BTreeSize(root->left); // ++count; // BTreeSize(root->right); //} 3.打印二叉树的结点的个数(后序打印） //int count = 0; //void BTreeSize(BTNode* root) //{ // if (root == NULL) // return; // BTreeSize(root->left); // BTreeSize(root->right); // ++count; //} 总结：以上定义成局部变量，静态局部变量都不够好！ 1.count定义成静态局部变量，每次调用无法初始化为0，当多次打印会出现累加计数 因此count应采用全局变量或者定义成静态全局变量 2.count定义成全局变量，会涉及到线程安全问题，这涉及到Linux的内容 写法4：将count定义成静态全局变量（可以打印） //static int count = 0; //int BTreeSize(BTNode* root) //{ // if (root == NULL) // return count; // BTreeSize(root->left); // BTreeSize(root->right); // ++count; // return count; //} 写法5：count既不定义成局部变量，也不定义成全局变量 思想：遍历+计数 将一个变量的地址传过去, 前序计数打印为例 //void BTreeSize(BTNode* root, int* pCount) //{ // if (root == NULL) // return; // ++(*pCount); // BTreeSize(root->left, pCount); // BTreeSize(root->right, pCount); //} //写法6：count既不定义成局部变量，也不定义成全局变量 //分治思想 //前序计数打印为例 int BTreeSize(BTNode* root) { return root == NULL ? 0 : BTreeSize(root->left) + BTreeSize(root->right) + 1; } //二、打印二叉树叶子结点的个数 //思路1：遍历+计数 //思路2：分治思想 //分治实现 int BTreeLeafSize(BTNode* root) { if (root == NULL) return 0; if (root->left == NULL && root->right == NULL) return 1; return BTreeLeafSize(root->left) + BTreeLeafSize(root->right); } //三、打印二叉树第k层的结点的个数 int BTreeKLevelSize(BTNode* root, int k) { assert(k >= 1); if (root == NULL) return 0; if (k == 1) return 1; return BTreeKLevelSize(root->left, k - 1) + BTreeKLevelSize(root->right, k - 1); } //四、打印二叉树的深度（高度） int BTreeDepth(BTNode* root) { if (root == NULL) return 0; int leftDepth = BTreeDepth(root->left); int rightDepth = BTreeDepth(root->right); return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1; } //五、二叉树查找值x的结点 //找到了就返回调用处，层层返回，直至首次调用，而不是直接返回打印！ BTNode* BTreeFind(BTNode* root, BTDataType x) { //树形结构实现查找 //以前序遍历为例 if (root == NULL) return NULL; if (root->data == x) return root; //写法1： //BTNode* ret1 = BTreeFind(root->left, x); //if (ret1) // return ret1; //BTNode* ret2 = BTreeFind(root->right, x); //if (ret2) // return ret2; 写法2：使用三目运算符 return (BTreeFind(root->left, x))? BTreeFind(root->left, x):BTreeFind(root->right, x); //或者 //return (BTreeFind(root->right, x)) ? BTreeFind(root->right, x) : BTreeFind(root->left, x); //写法3： //BTNode* ret1 = BTreeFind(root->left, x); //if (ret1) // return ret1; //return (BTreeFind(root->right, x)); /*//虽然可以正确打印，但这样就破坏了二叉树的遍历顺序 不可取 BTNode* ret2 = BTreeFind(root->right, x); if (ret2) return ret2; return (BTreeFind(root->left, x));*/ return NULL; } //六、二叉树的销毁 //思想：后序遍历进行销毁 //传一级指针无需置空，置空无用 //传二级指针需要置空 void BTreeDestroy(BTNode* root) { if (root == NULL) return; BTreeDestroy(root->left); BTreeDestroy(root->right); free(root); //root = NULL; //传一级指针置空不起作用 } 七、层序遍历 借助队列 void LevelOrder(BTNode* root) { Queue q; QueueInit(&q); if (root) { QueuePush(&q, root); } while (!QueueEmpty(&q)) { BTNode* front = QueueFront(&q); QueuePop(&q); printf("%d ", front->data); if (front->left) QueuePush(&q, front->left); if (front->right) QueuePush(&q, front->right); } printf("\n"); QueueDestroy(&q); } //八、判断二叉树是否为完全二叉树 //bool值类型 //return false<==>0<==>假 //return true<==>1<==>真 bool BTreeComplete(BTNode* root) { Queue q; QueueInit(&q); if (root) { QueuePush(&q, root); } while (!QueueEmpty(&q)) { BTNode* front = QueueFront(&q); QueuePop(&q); if (front == NULL) break; QueuePush(&q, front->left); QueuePush(&q, front->right); } while (!QueueEmpty(&q)) { BTNode* front = QueueFront(&q); QueuePop(&q); //遍历到空值，若后面又遍历到非空，那么说明不是完全二叉树 if (front) { //判断后需要销毁队列，否则就会造成内存泄漏 QueueDestroy(&q); printf("此二叉树不是完全二叉树\n"); return false; } } //判断后需要销毁队列，否则就会造成内存泄漏 QueueDestroy(&q); printf("此二叉树是完全二叉树\n"); return true; } int main() { BTNode* tree = CreatBinaryTree(); PreOrder(tree); //前序遍历打印 InOrder(tree); //中序遍历打印 PostOrder(tree); //后序遍历打印 //1.结点计数count定义成静态局部变量打印方式 //printf("二叉树结点个数:%d \n", BTreeSize(tree)); //printf("二叉树结点个数:%d \n", BTreeSize(tree)); //printf("二叉树结点个数:%d \n", BTreeSize(tree)); 2.结点计数count定义成全局变量打印方式 //count = 0; //BTreeSize(tree); //printf("二叉树结点个数:%d \n", count); //count = 0; //BTreeSize(tree); //printf("二叉树结点个数:%d \n", count); //count = 0; //BTreeSize(tree); //printf("二叉树结点个数:%d \n", count); 3.结点计数count定义成静态全局变量打印方式 //count = 0; //BTreeSize(tree); //printf("二叉树结点个数:%d \n", count); //count = 0; //BTreeSize(tree); //printf("二叉树结点个数:%d \n", count); // //count = 0; //BTreeSize(tree); //printf("二叉树结点个数:%d \n", count); //4.结点计数count既不定义成局部变量，也不定义成全局变量打印方式 //思想：遍历+计数 //int count1 = 0; //BTreeSize(tree, &count1); //printf("二叉树结点个数:%d \n", count1); //int count2 = 0; //BTreeSize(tree, &count2); //printf("二叉树结点个数:%d \n", count2); //int count3 = 0; //BTreeSize(tree, &count3); //printf("二叉树结点个数:%d \n", count3); 5.结点计数count分治思想打印 printf("二叉树结点个数:%d \n", BTreeSize(tree)); printf("二叉树结点个数:%d \n", BTreeSize(tree)); printf("二叉树结点个数:%d \n", BTreeSize(tree)); //6.二叉树叶子结点个数打印 //分治思想 printf("二叉树叶子结点个数:%d \n", BTreeLeafSize(tree)); //7.二叉树第k层结点数打印 //int level = 1; //打印第1层结点个数 //int level = 2; //打印第2层结点个数 int level = 3; //打印第3层结点个数 BTreeKLevelSize(tree, level); printf("二叉树第k层结点个数:%d \n", level); //8.二叉树的深度打印方式 printf("二叉树深度:%d \n", BTreeDepth(tree)); //9.二叉树的值x的查找打印方式 for (int i = 1; i <= 7; ++i) { printf("Find:%d,%p\n", i, BTreeFind(tree, i)); } //查找后修改 //返回结点指针的另一层含义—可修改其值 BTNode* ret = BTreeFind(tree, 5); if (ret) { ret->data = 50; } PreOrder(tree); printf("\n"); //10.层序遍历打印 LevelOrder(tree); //11.判断是否为完全二叉树打印 //因为使用bool值，0--假 1--真 //0--假(不是完全二叉树） //1--真(是完全二叉树) //打印方式1 BTreeComplete(tree); //打印方式2 //printf("完全二叉树：%d\n", BTreeComplete(tree)); //销毁二叉树 BTreeDestroy(tree); tree = NULL; return 0; } 附用队列实现源码：
Queue.h：
#pragma once //队列（链式）的功能实现 #include#include #include #include //typedef int QDataType; //层序遍历借助队列，只需将队列中的结构体中的int 更改为BTNode* //但会进行报错，因为编译器对定义的结构体类型，只会向上查找，对应 //typedef BTNode* QDataType; //以下写法可解决前述问题 //前置声明 //意思是告知编译器，此处定义的结构体可在头文件展开 struct BinaryTreeNode; typedef struct BinaryTreeNode* QDataType; typedef struct QueueNode { QDataType data; struct QueueNode* next; }QNode; //定义第二个结构体的原因是因为要方便队尾的插入，删除的管理 typedef struct Queue { QNode* head; QNode* tail; //size_t size; //若经常使用，可在此增加一个计数 }Queue; //初始化队列 void QueueInit(Queue* pq); //销毁 void QueueDestroy(Queue* pq); //插入（进队） void QueuePush(Queue* pq, QDataType x); //删除（出队） void QueuePop(Queue* pq); //判断队列是否为空 bool QueueEmpty(Queue* pq); //队列大小 size_t QueueSize(Queue* pq); //size_t即unsigned int，包含在头文件 //队头 QDataType QueueFront(Queue* pq); //队尾 QDataType QueueBack(Queue* pq); Queue.c：
#include "Queue.h" //队列（链式）的功能实现 //队列的功能函数 //初始化队列 void QueueInit(Queue* pq) { assert(pq); pq->head = pq->tail = NULL; } //销毁 void QueueDestroy(Queue* pq) { assert(pq); QNode* cur = pq->head; while (cur) { QNode* next = cur->next; free(cur); cur = next; } pq->head = pq->tail = NULL; } //插入（进队） void QueuePush(Queue* pq, QDataType x) { assert(pq); //开辟新结点 QNode* newnode = (QNode*)malloc(sizeof(QNode)); assert(newnode); newnode->data = x; newnode->next = NULL; if (pq->tail == NULL) { assert(pq->head == NULL); pq->head = pq->tail = newnode; } else { pq->tail->next = newnode; pq->tail = newnode; } } //删除（出队） void QueuePop(Queue* pq) { assert(pq); assert(pq->head && pq->tail); if (pq->head->next == NULL) { free(pq->head); pq->head = pq->tail = NULL; } else { QNode* next = pq->head->next; free(pq->head); pq->head = next; } } //判断队列是否为空 bool QueueEmpty(Queue* pq) { assert(pq); //return pq->head == NULL && pq->tail == NULL; return pq->head == NULL; } //队列大小 //size_t即unsigned int，包含在头文件 size_t QueueSize(Queue* pq) { assert(pq); QNode* cur = pq->head; size_t size = 0; while (cur) { size++; cur = cur->next; } return size; //如果经常使用size，可以在结构体中定义size， //然后初始化为0，就不用在使用while计算 //这样就不用遍历，降低时间复杂度 } //队头 QDataType QueueFront(Queue* pq) { assert(pq); assert(pq->head); return pq->head->data; } //队尾 QDataType QueueBack(Queue* pq) { assert(pq); assert(pq->tail); return pq->tail->data; }