Python sort原理

引言

sort内部实现：Timesort

最坏时间复杂度：$O(nlogn)$

空间复杂度：$O(n)$

内部实现原理的回答

1. python sort 函数采用的排序算法_知乎：其中一个回答提到了 python 中的 sorted 排序内部实现是 timsort，并没有说 sort 。

2. python的sorted排序分析_Github： 同样只提到了 python 中的 sorted 排序内部实现是 timsort，并没有说 sort （知乎回答的一个链接）。

3. C++，java,Python的内部实现sort怎么实现的_CSDN：内容提到 python内部的sort采用的是混合（hybrid）排序，规模小的时候采用 binary insertion，规模大的时候采用 sample sort 。

4. list.sort 方法和 sorted 函数_《流畅的Python》： 注7 中提到 python的排序算法——Timesort——是稳定的，意思是就算两个元素比不出大小，在每次排序的结果里他们的相对位置是固定的。

以上大量回答都指向Timsort，那么就继续看看这是个啥

Timesort

维基百科：Timsort是结合了合并排序（merge sort）和插入排序（insertion sort）而得出的排序算法，它在现实中有很好的效率。Tim Peters在2002年设计了该算法并在Python中使用（TimSort 是 Python 中 list.sort 的默认实现）。该算法找到数据中已经排好序的块-分区，每一个分区叫一个run，然后按规则合并这些run。Pyhton自从2.3版以来一直采用Timsort算法排序，现在Java SE7和Android也采用Timsort算法对数组排序。

操作

1.1 run的最小长度

1.2 优化run的长度

1.3 合并run

1.4 合并步骤

1.5 Galloping模型

性能

Timesort核心过程：

TimSort 算法为了减少对升序部分的回溯和对降序部分的性能倒退，将输入按其升序和降序特点进行了分区。排序的输入的单位不是一个个单独的数字，而是一个个的块-分区。其中每一个分区叫一个run。针对这些 run 序列，每次拿一个 run 出来按规则进行合并。每次合并会将两个 run合并成一个 run。合并的结果保存到栈中。合并直到消耗掉所有的 run，这时将栈上剩余的 run合并到只剩一个 run 为止。这时这个仅剩的 run 便是排好序的结果。

综上述过程，Timsort算法的过程包括

（0）如果数组长度小于某个值，直接用二分插入排序算法

（1）找到各个run，并入栈

（2）按规则合并run

操作

现实中的大多数据通常是有部分已经排好序的，Timsort利用了这一特点。Timsort排序的输入单位不是一个个单独的数字，而是一个个的分区。其中每一个分区叫一个run（图1）。针对这个 run 序列，每次拿一个 run 出来进行归并。每次归并会将两个 run 合并成一个 run。每个run最少要有2个元素。Timesor按照升序和降序划分出各个run：run如果是升序的，那么run中的后一元素要大于或等于前一元素（a[lo] <= a[lo + 1] <= a[lo + 2] <= ...）；如果run是严格降序的，即run中的前一元素大于后一元素（a[lo] > a[lo + 1] > a[lo + 2] > ...），需要将run 中的元素翻转（这里注意降序的部分必须是“严格”降序才能进行翻转。因为 TimSort 的一个重要目标是保持稳定性stability。如果在 >= 的情况下进行翻转这个算法就不再是stable）。

run的最小长度

run是已经排好序的一块分区。run可能会有不同的长度，Timesort根据run的长度来选择排序的策略。例如：

如果run的长度小于某一个值，则会选择插入排序算法来排序。run的最小长度（minrun）取决于数组的大小。当数组元素少于64个时，那么run的最小长度便是数组的长度，这时Timsort用插入排序算法来排序；

当数组元素大于等于63时，对于较大的阵列，从32到65范围选择的一个数字，称为Minrun，使得数组的大小除以最小run大小，等于或略小于2的幂。最终算法只取数组大小的六个最高有效位。如果设置了任何保留位，则加1，并将将结果作为minrun。该算法适用于所有情况，包括数组大小小于64的算法。

图1 run

优化run的长度

优化run的长度是指当run的长度小于minrun时，为了使这样的run的长度达到minrun的长度，会从数组中选择合适的元素插入run中。这样做使大部分的run的长度达到均衡，有助于后面run的合并操作。

合并run

划分run和优化run长度以后，然后就是对各个run进行合并。合并run的原则：

run合并的技术要保证有最高的效率。当Timsort算法找到一个run时，会将该run在数组中的起始位置和run的长度放入栈中，然后根据先前放入栈中的run决定是否该合并run。Timsort不会合并在栈中不连续的run（Timsort不会合并非连续run，因为这样做会导致所有三个run共有的元素相对于中间run变得混乱）

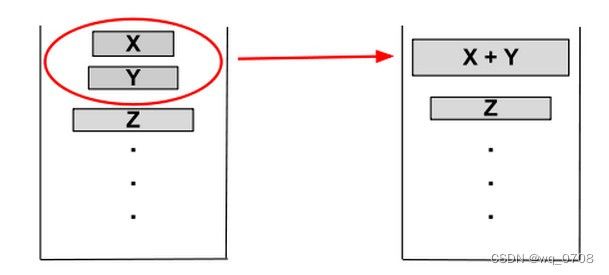
Timsort会合并在栈中2个连续的run。X、Y、Z代表栈最上方的3个run的长度（图2），当同时不满足下面2个条件是，X、Y这两个run会被合并，直到同时满足下面2个条件，则合并结束：

$$\begin{gathered} (1)X>Y+Z \\ (2)Y>Z \end{gathered}$$

例如：如果$X<Y+Z$，那么$X+Y$合并为一个新的run，然后入栈。重复上述步骤，直到同时满足上述2个条件。当合并结束后，Timsort会继续找下一run，然后找到以后入栈，重复上述步骤，及每次run入栈都会检查是否需要合并2个run。

图2 合并run

合并run

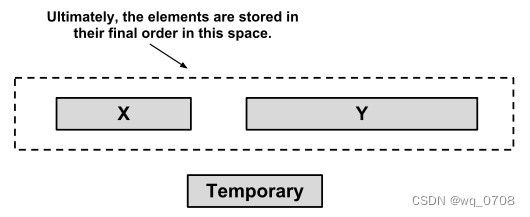
合并2个相邻的run需要临时存储空闲，临时存储空间的大小是2个run中较小的run的大小。Timsort算法先将较小的run复制到这个临时存储空间，然后用原先存储这2个run的空间来存储合并后的run（图3）。

图3 临时存储空间

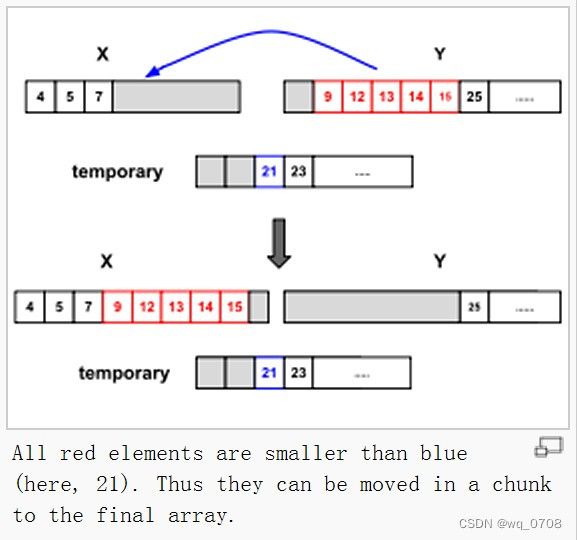
简单的合并算法是用简单插入算法，依次从左到右或从右到左比较，然后合并2个run。为了提高效率，Timsort用二分插入算法（binary merge sort）。先用二分查找算法/折半查找算法（binary search）找到插入的位置，然后再插入。

例如，我们要将A和B这2个run合并，且A是较小的run。因为A和B已经分别是排好序的，二分查找会找到B的第一个元素在A中何处插入（图4）。同样，A的最后一个元素找到在B的何处插入，找到以后，B在这个元素之后的元素就不需要比较了（图5）。这种查找可能在随机数中效率不会很高，但是在其他情况下有很高的效率。

图4 run合并过程1

图5 run合并过程2

Galloping模型

类似上述run的合并过程，参见维基百科Galloping Model

性能

根据信息学理论，在平均情况下，比较排序不会比$O(nlogn)$更快。由于Timsort算法利用了现实中大多数数据中会有一些排好序的区，所以Timsort会比
$O(nlogn)$快些。对于随机数没有可以利用的排好序的区，Timsort时间复杂度会是$log(n!)$。

Timesort与其他比较排序算法的性能比较

说明

JSE 7对对象进行排序，没有采用快速排序，是因为快速排序是不稳定的，而Timsort是稳定的。

下面是JSE7 中Timsort实现代码中的一段话，可以很好的说明Timsort的优势：

A stable, adaptive, iterative mergesort that requires far fewer than n lg(n) comparisons when running on partially sorted arrays, while offering performance comparable to a traditional mergesort when run on random arrays. Like all proper mergesorts, this sort is stable and runs O(n log n) time (worst case). In the worst case, this sort requires temporary storage space for n/2 object references; in the best case, it requires only a small constant amount of space.

大体是说，Timsort是稳定的算法，当待排序的数组中已经有排序好的数，它的时间复杂度会小于$O(nlogn)$。与其他合并排序一样，Timesrot是稳定的排序算法，最坏时间复杂度是$O(nlogn)$。在最坏情况下，Timsort算法需要的临时空间是n/2，在最好情况下，它只需要一个很小的临时存储空间

参考

1. sort与sorted区别

2. Python3中自定义排序原理

3. Wiki/Timsort

4. Wiki/Samplesort

5. python 的内部排序算法list.sort

6. 什么是Timesort排序方法

7. Timsort原理介绍

8. 流畅的python/page-36

9. 关于Timsort算法的Bug(已经影响Android、Java、python不知道有没有被修复)