布隆过滤器介绍
布隆过滤器(Bloom Filter,下文简称BF)由Burton Howard Bloom在1970年提出,是一种空间效率高的概率型数据结构。它专门用来检测集合中是否存在特定的元素。听起来是很稀松平常的需求,为什么要使用BF这种数据结构呢?
产生的契机
回想一下,我们平常在检测集合中是否存在某元素时,都会采用比较的方法。考虑以下情况:
如果集合用线性表存储,查找的时间复杂度为O(n)。
如果用平衡BST(如AVL树、红黑树)存储,时间复杂度为O(logn)。
-
如果用哈希表存储,并用链地址法与平衡BST解决哈希冲突(参考JDK8的HashMap实现方法),时间复杂度也要有O[log(n/m)],m为哈希分桶数。
 image
image
总而言之,当集合中元素的数量极多时,不仅查找会变得很慢,而且占用的空间也会大到无法想象。BF就是解决这个矛盾的利器。
设计思想
BF是由一个长度为m比特的位数组(bit array)与k个哈希函数(hash function)组成的数据结构。位数组均初始化为0,所有哈希函数都可以分别把输入数据尽量均匀地散列。
当要插入一个元素时,将其数据分别输入k个哈希函数,产生k个哈希值。以哈希值作为位数组中的下标,将所有k个对应的比特置为1。
当要查询(即判断是否存在)一个元素时,同样将其数据输入哈希函数,然后检查对应的k个比特。如果有任意一个比特为0,表明该元素一定不在集合中。如果所有比特均为1,表明该集合有(较大的)可能性在集合中。为什么不是一定在集合中呢?因为一个比特被置为1有可能会受到其他元素的影响,这就是所谓“假阳性”(false positive)。相对地,“假阴性”(false negative)在BF中是绝不会出现的。
下图示出一个m=18, k=3的BF示例。集合中的x、y、z三个元素通过3个不同的哈希函数散列到位数组中。当查询元素w时,因为有一个比特为0,因此w不在该集合中。
优缺点与用途
BF的优点是显而易见的:
- 不需要存储数据本身,只用比特表示,因此空间占用相对于传统方式有巨大的优势,并且能够保密数据;
- 时间效率也较高,插入和查询的时间复杂度均为O(k);
- 哈希函数之间相互独立,可以在硬件指令层面并行计算。
但是,它的缺点也同样明显:
- 存在假阳性的概率,不适用于任何要求100%准确率的情境;
- 只能插入和查询元素,不能删除元素,这与产生假阳性的原因是相同的。我们可以简单地想到通过计数(即将一个比特扩展为计数值)来记录元素数,但仍然无法保证删除的元素一定在集合中。
所以,BF在对查准度要求没有那么苛刻,而对时间、空间效率要求较高的场合非常合适,本文第一句话提到的用途即属于此类。另外,由于它不存在假阴性问题,所以用作“不存在”逻辑的处理时有奇效,比如可以用来作为缓存系统(如Redis)的缓冲,防止缓存穿透。
假阳性率的计算
假阳性是BF最大的痛点,因此有必要权衡,比如计算一下假阳性的概率。为了简单一点,就假设我们的哈希函数选择位数组中的比特时,都是等概率的。当然在设计哈希函数时,也应该尽量满足均匀分布。
在位数组长度m的BF中插入一个元素,它的其中一个哈希函数会将某个特定的比特置为1。因此,在插入元素后,该比特仍然为0的概率是:
现有k个哈希函数,并插入n个元素,自然就可以得到该比特仍然为0的概率是:
反过来讲,它已经被置为1的概率就是:
也就是说,如果在插入n个元素后,我们用一个不在集合中的元素来检测,那么被误报为存在于集合中的概率(也就是所有哈希函数对应的比特都为1的概率)为:
当n比较大时,根据重要极限公式,可以近似得出假阳性率:
所以,在哈希函数的个数k一定的情况下:
- 位数组长度m越大,假阳性率越低;
- 已插入元素的个数n越大,假阳性率越高。
事实上,即使哈希函数不是等概率选择比特的,最终也会得出相同的结果,可以借助吾妻-霍夫丁不等式(Azuma-Hoeffding inequality)证明。我数学比较垃圾,就不班门弄斧了。
有一些框架内已经内建了BF的实现,免去了自己实现的烦恼。下面以Guava为例,看看Google是怎么做的。
Guava中的布隆过滤器
采用Guava 27.0.1版本的源码,BF的具体逻辑位于com.google.common.hash.BloomFilter类中。开始读代码吧。
BloomFilter类的成员属性
不多,只有4个。
/** The bit set of the BloomFilter (not necessarily power of 2!) */
private final LockFreeBitArray bits;
/** Number of hashes per element */
private final int numHashFunctions;
/** The funnel to translate Ts to bytes */
private final Funnel funnel;
/** The strategy we employ to map an element T to {@code numHashFunctions} bit indexes. */
private final Strategy strategy;
- bits即上文讲到的长度为m的位数组,采用LockFreeBitArray类型做了封装。
- numHashFunctions即哈希函数的个数k。
- funnel是Funnel接口实现类的实例,它用于将任意类型T的输入数据转化为Java基本类型的数据(byte、int、char等等)。这里是会转化为byte。
- strategy是布隆过滤器的哈希策略,即数据如何映射到位数组,其具体方法在BloomFilterStrategies枚举中。
BloomFilter的构造
这个类的构造方法是私有的。要创建它的实例,应该通过公有的create()方法。它一共有5种重载方法,但最终都是调用了如下的逻辑。
@VisibleForTesting
static BloomFilter create(
Funnel funnel, long expectedInsertions, double fpp, Strategy strategy) {
checkNotNull(funnel);
checkArgument(
expectedInsertions >= 0, "Expected insertions (%s) must be >= 0", expectedInsertions);
checkArgument(fpp > 0.0, "False positive probability (%s) must be > 0.0", fpp);
checkArgument(fpp < 1.0, "False positive probability (%s) must be < 1.0", fpp);
checkNotNull(strategy);
if (expectedInsertions == 0) {
expectedInsertions = 1;
}
/*
* TODO(user): Put a warning in the javadoc about tiny fpp values, since the resulting size
* is proportional to -log(p), but there is not much of a point after all, e.g.
* optimalM(1000, 0.0000000000000001) = 76680 which is less than 10kb. Who cares!
*/
long numBits = optimalNumOfBits(expectedInsertions, fpp);
int numHashFunctions = optimalNumOfHashFunctions(expectedInsertions, numBits);
try {
return new BloomFilter(new LockFreeBitArray(numBits), numHashFunctions, funnel, strategy);
} catch (IllegalArgumentException e) {
throw new IllegalArgumentException("Could not create BloomFilter of " + numBits + " bits", e);
}
}
该方法接受4个参数:funnel是插入数据的Funnel,expectedInsertions是期望插入的元素总个数n,fpp即期望假阳性率p,strategy即哈希策略。
由上可知,位数组的长度m和哈希函数的个数k分别通过optimalNumOfBits()方法和optimalNumOfHashFunctions()方法来估计。
估计最优m值和k值
@VisibleForTesting
static long optimalNumOfBits(long n, double p) {
if (p == 0) {
p = Double.MIN_VALUE;
}
return (long) (-n * Math.log(p) / (Math.log(2) * Math.log(2)));
}
@VisibleForTesting
static int optimalNumOfHashFunctions(long n, long m) {
// (m / n) * log(2), but avoid truncation due to division!
return Math.max(1, (int) Math.round((double) m / n * Math.log(2)));
}
要看懂这两个方法,我们得接着上一节的推导继续做下去。
由假阳性率的近似计算方法可知,如果要使假阳性率尽量小,在m和n给定的情况下,k值应为:
这就是optimalNumOfHashFunctions()方法的逻辑。那么m该如何估计呢?
将k代入上一节的式子并化简,我们可以整理出期望假阳性率p与m、n的关系:
亦即:
这就是optimalNumOfBits()方法的逻辑。
从上也可以得出:
如果指定期望假阳性率p,那么最优的m值与期望元素数n呈线性关系。
-
最优的k值实际上只与p有关,与m和n都无关,即:
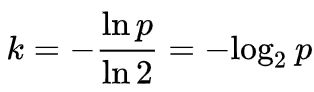 image
image
所以,在创建BloomFilter时,确定合适的p和n值很重要。
哈希策略
在BloomFilterStrategies枚举中定义了两种哈希策略,都基于著名的MurmurHash算法,分别是MURMUR128_MITZ_32和MURMUR128_MITZ_64。前者是一个简化版,所以我们来看看后者的实现方法。
MURMUR128_MITZ_64() {
@Override
public boolean put(
T object, Funnel funnel, int numHashFunctions, LockFreeBitArray bits) {
long bitSize = bits.bitSize();
byte[] bytes = Hashing.murmur3_128().hashObject(object, funnel).getBytesInternal();
long hash1 = lowerEight(bytes);
long hash2 = upperEight(bytes);
boolean bitsChanged = false;
long combinedHash = hash1;
for (int i = 0; i < numHashFunctions; i++) {
// Make the combined hash positive and indexable
bitsChanged |= bits.set((combinedHash & Long.MAX_VALUE) % bitSize);
combinedHash += hash2;
}
return bitsChanged;
}
@Override
public boolean mightContain(
T object, Funnel funnel, int numHashFunctions, LockFreeBitArray bits) {
long bitSize = bits.bitSize();
byte[] bytes = Hashing.murmur3_128().hashObject(object, funnel).getBytesInternal();
long hash1 = lowerEight(bytes);
long hash2 = upperEight(bytes);
long combinedHash = hash1;
for (int i = 0; i < numHashFunctions; i++) {
// Make the combined hash positive and indexable
if (!bits.get((combinedHash & Long.MAX_VALUE) % bitSize)) {
return false;
}
combinedHash += hash2;
}
return true;
}
private /* static */ long lowerEight(byte[] bytes) {
return Longs.fromBytes(
bytes[7], bytes[6], bytes[5], bytes[4], bytes[3], bytes[2], bytes[1], bytes[0]);
}
private /* static */ long upperEight(byte[] bytes) {
return Longs.fromBytes(
bytes[15], bytes[14], bytes[13], bytes[12], bytes[11], bytes[10], bytes[9], bytes[8]);
}
};
其中put()方法负责向布隆过滤器中插入元素,mightContain()方法负责判断元素是否存在。以put()方法为例讲解一下流程吧。
- 使用MurmurHash算法对funnel的输入数据进行散列,得到128bit(16B)的字节数组。
- 取低8字节作为第一个哈希值hash1,取高8字节作为第二个哈希值hash2。
- 进行k次循环,每次循环都用hash1与hash2的复合哈希做散列,然后对m取模,将位数组中的对应比特设为1。
这里需要注意两点:
-
在循环中实际上应用了双重哈希(double hashing)的思想,即可以用两个哈希函数来模拟k个,其中i为步长:
 image
image这种方法在开放定址的哈希表中,也经常用来减少冲突。
哈希值有可能为负数,而负数是不能在位数组中定位的。所以哈希值需要与Long.MAX_VALUE做bitwise AND,直接将其最高位(符号位)置为0,就变成正数了。
位数组具体实现
来看LockFreeBitArray类的部分代码。
static final class LockFreeBitArray {
private static final int LONG_ADDRESSABLE_BITS = 6;
final AtomicLongArray data;
private final LongAddable bitCount;
LockFreeBitArray(long bits) {
this(new long[Ints.checkedCast(LongMath.divide(bits, 64, RoundingMode.CEILING))]);
}
// Used by serialization
LockFreeBitArray(long[] data) {
checkArgument(data.length > 0, "data length is zero!");
this.data = new AtomicLongArray(data);
this.bitCount = LongAddables.create();
long bitCount = 0;
for (long value : data) {
bitCount += Long.bitCount(value);
}
this.bitCount.add(bitCount);
}
/** Returns true if the bit changed value. */
boolean set(long bitIndex) {
if (get(bitIndex)) {
return false;
}
int longIndex = (int) (bitIndex >>> LONG_ADDRESSABLE_BITS);
long mask = 1L << bitIndex; // only cares about low 6 bits of bitIndex
long oldValue;
long newValue;
do {
oldValue = data.get(longIndex);
newValue = oldValue | mask;
if (oldValue == newValue) {
return false;
}
} while (!data.compareAndSet(longIndex, oldValue, newValue));
// We turned the bit on, so increment bitCount.
bitCount.increment();
return true;
}
boolean get(long bitIndex) {
return (data.get((int) (bitIndex >>> 6)) & (1L << bitIndex)) != 0;
}
// ....
}
看官应该能明白为什么它要叫做“LockFree”BitArray了,因为它是采用原子类型AtomicLongArray作为位数组的存储的,确实不需要加锁。另外还有一个Guava中特有的LongAddable类型的计数器,用来统计置为1的比特数。
采用AtomicLongArray除了有并发上的优势之外,更主要的是它可以表示非常长的位数组。一个长整型数占用64bit,因此data[0]可以代表第063bit,data[1]代表64127bit,data[2]代表128~191bit……依次类推。这样设计的话,将下标i无符号右移6位就可以获得data数组中对应的位置,再在其基础上左移i位就可以取得对应的比特了。
最后多嘴一句,上面的代码中用到了Long.bitCount()方法计算long型二进制表示中1的数量,堪称Java语言中最强的骚操作之一:
public static int bitCount(long i) {
// HD, Figure 5-14
i = i - ((i >>> 1) & 0x5555555555555555L);
i = (i & 0x3333333333333333L) + ((i >>> 2) & 0x3333333333333333L);
i = (i + (i >>> 4)) & 0x0f0f0f0f0f0f0f0fL;
i = i + (i >>> 8);
i = i + (i >>> 16);
i = i + (i >>> 32);
return (int)i & 0x7f;
}
总结
本文讲解了布隆过滤器的产生、设计思路和应用场景,通过简单推导明确了其假阳性问题。另外,又通过阅读Guava中BloomFilter的相关源码,了解了设计布隆过滤器的技术要点。之后还会另外写文章讲述我们在生产环境中的具体应用。
原文链接:https://www.jianshu.com/p/bef2ec1c361f