神经网络——机器学习(周志华)
C++实现神经网络
神经网络
神经元模型
神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。
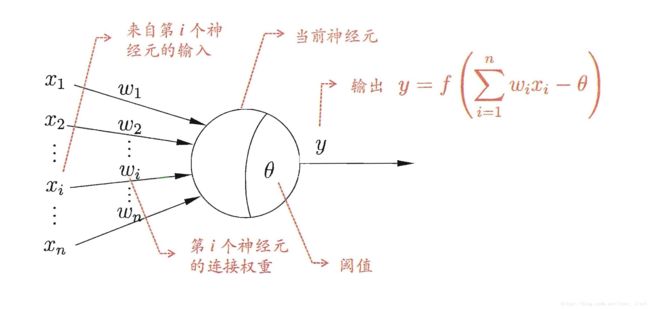
感知机与多层网络
y = f ( ∑ i ω i x i − θ ) y = f(\sum_i \omega_i x_i - \theta) y=f(i∑ωixi−θ)
感知机油两层神经元组成,权重 ω i ( i = 1 , 2 , . . . , n ) \omega_i(i = 1,2,...,n) ωi(i=1,2,...,n)以及阈值 θ \theta θ可通过学习得到,阈值 θ \theta θ可看作是一个固定输入为-1.0得节点所对应得连接权重是 ω n + 1 \omega_{n+1} ωn+1,这样权重和阈值得学习就可统一为权重得学习。权重调整为
ω i = ω i + Δ ω i Δ ω i = η ( y − y ^ ) x i \omega_i= \omega_i + \Delta\omega_i \\ \Delta\omega_i = \eta(y-\widehat{y})x_i ωi=ωi+ΔωiΔωi=η(y−y )xi
η ∈ ( 0 , 1 ) \eta \in (0,1) η∈(0,1)称为学习率
感知机只有输出层神经元进行激活函数处理,即只拥有一层功能神经元。(解决线性可分问题)
要解决非线性可分问题,要使用多层功能得神经元。
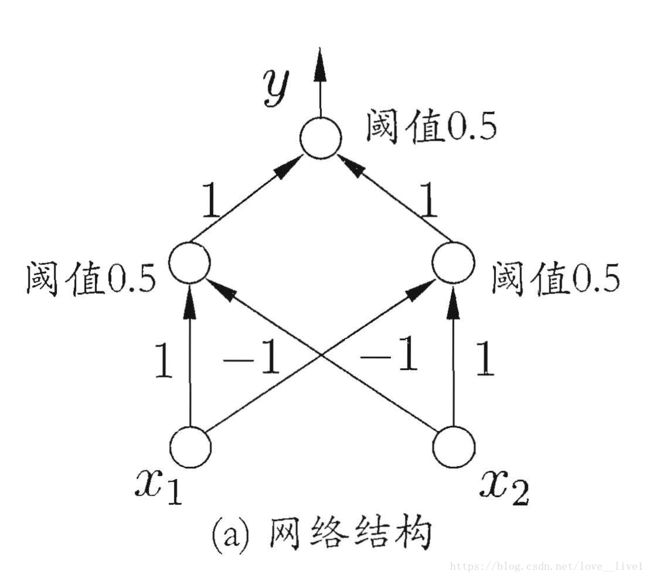
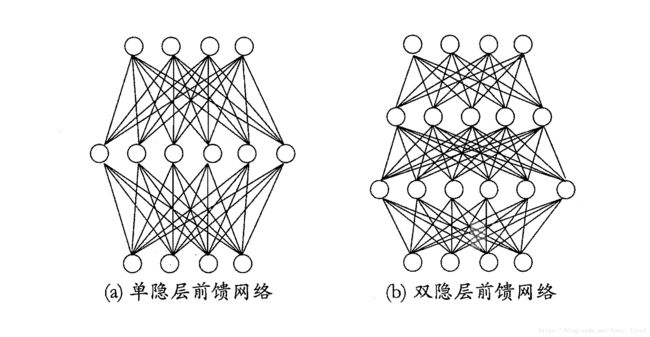
误差逆传播算法(BP)

给定训练集 D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) , x i ∈ R d , y i ∈ R l D=\bm{{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)}, x_i \in \mathbb{R}^d, y_i \in \mathbb{R}^l} D=(x1,y1),(x2,y2),...,(xm,ym),xi∈Rd,yi∈Rl,即输入由 d d d个属性描述,输出 l l l维实值向量
假设隐层和输出层都是用Sigmod函数。
θ j \theta_j θj:输出层第j 个神经元的阀值
γ h \gamma_h γh:隐层第h 个神经元的阔值
v i h v_{ih} vih:输入层第t 个神经元与隐居第h 个神经元之间的连接权
ω h j \omega_{hj} ωhj:,隐层第h 个神经元与输出层第j 个神经元之间的连接权
BP算法推导过程
- 对于训练集 ( x k , y k ) \bm{(x_k,y_k)} (xk,yk),假设圣经网络得输出为 y ^ k = ( y ^ 1 k , y ^ 2 k , . . . , y ^ l k ) \bm{\widehat{y}_k} = (\widehat{y}_1^k, \widehat{y}_2^k, ...,\widehat{y}_l^k) y k=(y 1k,y 2k,...,y lk),即
y ^ j k = f ( β j − θ j ) \widehat{y}_j^k=f(\beta_j - \theta_j) y jk=f(βj−θj) - 在 ( x k , y k ) \bm{(x_k,y_k)} (xk,yk)上得均方差为
E k = 1 2 ∑ j = 1 l ( y ^ j k − y j k ) E_k = \frac{1}{2} \sum_{j=1}^l(\widehat{y}_j^k - y_j^k) Ek=21j=1∑l(y jk−yjk) - 基于梯度下降策略,对误差 E k E_k Ek,给定学习率 η \eta η
Δ ω h , j = − η ∂ E k ∂ ω h , j ∂ E k ∂ ω h , j = − ∂ E k ∂ y ^ j k . ∂ y ^ j k ∂ β j . ∂ β j ∂ ω h , j \Delta\omega_{h,j} = -\eta\frac{\partial{E_k}}{\partial{\omega_{h,j}}} \\ \frac{\partial{E_k}}{\partial{\omega_{h,j}}} = -\frac{\partial{E_k}}{\partial{\widehat{y}_j^k}} .\frac{\partial{\widehat{y}_j^k}}{\partial{\beta_j}} .\frac{\partial{\beta_j}}{\partial{\omega_{h,j}}} Δωh,j=−η∂ωh,j∂Ek∂ωh,j∂Ek=−∂y jk∂Ek.∂βj∂y jk.∂ωh,j∂βj - 令 b h = ∂ β j ∂ ω h , j b_h = \frac{\partial{\beta_j}}{\partial{\omega_{h,j}}} bh=∂ωh,j∂βj
S i g m o d Sigmod Sigmod函数性质: f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f^{'}(x) = f(x)(1-f(x)) f′(x)=f(x)(1−f(x))
-
令
g i = − ∂ E k ∂ y ^ j k . ∂ y ^ j k ∂ β j = − ( y ^ j k − y j k ) f ′ ( β i − θ j ) = y ^ j k ( 1 − y ^ j k ) ( y ^ j k − y j k ) g_i = -\frac{\partial{E_k}}{\partial{\widehat{y}_j^k}} .\frac{\partial{\widehat{y}_j^k}}{\partial{\beta_j}} \\ = -(\widehat{y}_j^k - y_j^k)f^{'}(\beta_i - \theta_j) \\ = \widehat{y}_j^k(1-\widehat{y}_j^k)(\widehat{y}_j^k - y_j^k) gi=−∂y jk∂Ek.∂βj∂y jk=−(y jk−yjk)f′(βi−θj)=y jk(1−y jk)(y jk−yjk) -
得出
Δ ω h j = η g j b h \Delta\omega_{hj} = \eta g_jb_h Δωhj=ηgjbh
类似得出
θ j = − η g j v i h = η e h x i γ h = − η e h \theta_j = -\eta g_j \\ v_{ih}= \eta e_hx_i \\ \gamma_h = -\eta e_h θj=−ηgjvih=ηehxiγh=−ηeh
其中 e h = b h ( 1 − b h ) ∑ j = 1 l ω h j g j e_h = b_h(1-b_h)\sum_{j=1}^l\omega_{hj} g_j eh=bh(1−bh)∑j=1lωhjgj
BP算法得目标是要最小化训练集D上得累计误差
E = 1 m ∑ k = 1 m E k E = \frac{1}{m}\sum_{k=1}^{m}E_k E=m1k=1∑mEk
缓解过拟合策略
BP神经网络经常遭遇过拟合。
有两种策略常用来缓解BP网络得过拟合:
- “早停”:将数据集分成训练和验证集,训练集用来计算梯度、更新权重和阈值,验证集用来估计误差,若训练集误差降低但验证集误差升高,则停止训练,同时返回具有最小验证集误差得连接权和阈值。
- “正则化”:基本思想是在误差目标函数中增加一个用于描述网络复杂度得部分,例如权重和阈值得平方和:
E = λ 1 m ∑ k = 1 m E k + ( 1 − λ ) ∑ i ω i 2 E = \lambda \frac{1}{m}\sum_{k=1}^{m}E_k + (1 - \lambda)\sum_i\omega_i^2 E=λm1k=1∑mEk+(1−λ)i∑ωi2
ω i \omega_i ωi表示连接权和阈值, λ ∈ ( 0 , 1 ) \lambda\in(0, 1) λ∈(0,1)用于对经验误差与网络复杂度这两项进行折中,常通过交叉验证法来估计。
全局最小和局部最小
如图,如果误差函数仅有一个局部极小值,则这个就是全局最小,如果有多个局部极小值,则不能保证找到得解是全局最小。
解决方法:
- 以多组不同参数值初始化多个神经网络7 按标准方法训练后,取其中误差最小的解作为最终参数.这相当于从多个不同的初始点开始搜索, 这样就可能陷入不同的局部极小从中进行选择有可能获得更接近全局最小的结果.
- 使用"模拟退火" (simulated annealing) 技术[Aarts and Korst, 1989].模拟退火在每一步都以二定的概率接受比当前解更差的结果,从而有助于"跳出"局部极小. 在每步i主代过程中7 接受"次优解"的概率要随着时间的推移而逐渐降低7 从而保证算法稳定.
- 使用随机梯度下降.与标准梯度下降法精确计算梯度不同, 随机梯度下降法在计算梯度时加入了随机因素.于是?即便陷入局部极小点? 它计算出的梯度仍可能不为零3 这样就有机会跳出局部极小继续搜索.
此外, 遗传算法(genetic algorithms) [Goldberg, 1989] 也常用来训练神经网络以更好地逼近全局最小. 需注意的是?上述用于跳出局部极小的技术大多是启发式,理论七尚缺乏保障.
其他常见得神经网络
- RBF网络
- ART网络
- SOM网路
- 级联相关网络
- Elman网络
- Boltzmann机
深度学习
典型得深度学习模型就是很深层得神经网络。
增加隐层得数目。
但多隐层神经网络难以直接用经典BP算法训练,因为误差在对隐层逆传播时,往往会“发散”而不能收敛到稳定状态。