快速排序（非递归）以及归并排序的递归与非递归

快速排序的非递归算法：

递归次数太多的缺陷：极端情况下（栈帧深度太深）会导致栈溢出，即使程序代码正确（递归的深度足够深时，空间不足，就会导致栈溢出），因此在实际应用中通常情况下是利用非递归算法实现。

递归改成非递归：1.直接改循环（简单）2.借助数据结构栈模拟递归过程（复杂）

首先要建立一个栈，直接引用之前建立过的栈即可，用栈来模拟左右递归的过程，由于栈是先进的后出，为了先排左边的，就得先将被分割后的右边下标存入栈中，当左边的下标被提取完之后，说明左边已经有序，接着取出右边的下标进行单趟排序即可。以此类推：

快速排序非递归代码：

void QuickSortNoneR(int* a, int n)
{
	ST st;
	StackInit(&st);
	StackPush(&st, n - 1);
	StackPush(&st, 0);
	while (!StackEmpty(&st))
	{
		int left = StackTop(&st);
		StackPop(&st);
		int right = StackTop(&st);
		StackPop(&st);
		int keyIndex = PartSort1(a, left, right);
		//[left,keyIndex-1] keyIndex [keyIndex+1,right]
		if (keyIndex + 1 < right)
		{
			StackPush(&st, right);
			StackPush(&st, keyIndex + 1);
		}
		if (keyIndex - 1 > left)
		{
			StackPush(&st, keyIndex - 1);
			StackPush(&st, left);
		}
	}
	StackDestory(&st);
}

Stack.h

#pragma once
#include
#include
#include
#include
typedef int STDataType;
typedef struct Stack
{
	STDataType* a;
	int top;//栈顶
	int capacity;
}ST;
//初始化
void StackInit(ST* ps);
//销毁栈
void StackDestory(ST* ps);
//栈顶插入数据（入栈）
void StackPush(ST* ps,STDataType x);
//出栈
void StackPop(ST* ps);
STDataType StackTop(ST* ps);
int StackSize(ST* ps);
bool StackEmpty(ST* ps);

 Stack.c

#define _CRT_SECURE_NO_WARNINGS
#include"Stack.h"
//初始化
void StackInit(ST* ps)
{
	assert(ps);
	ps->a = (STDataType*)malloc(sizeof(STDataType) * 4);
	if (ps->a == NULL)
	{
		printf("malloc fail\n");
		exit(-1);//不是正常结束
	}
	ps->capacity = 4;
	ps->top = 0;//意味着top指向的是栈顶元素的下一位，若为-1，则top指向的是栈顶元素
}
//销毁栈
void StackDestory(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->top = 0; 
}
//栈顶插入数据（入栈）
void StackPush(ST* ps, STDataType x)
{
	assert(ps);
	if (ps->top == ps->capacity)
	{
		STDataType* tmp = (STDataType*)realloc(ps->a, ps->capacity * 2 * sizeof(STDataType));
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);//不是正常结束
		}
		else
		{
			ps->a = tmp;
			ps->capacity *= 2;
		}
	}
	ps->a[ps->top] = x;
	ps->top++;
}
//出栈
void StackPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);//栈空了，调用pop，直接中止程序报错
	ps->top--;
}
//返回栈顶元素
STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	return ps -> a[ps->top - 1];
}
//返回栈中数据的数量
int StackSize(ST* ps)
{
	assert(ps);
	return ps->top;
}
//判断是否为空
bool StackEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}

我对于快速排序的非递归说的不太详细，大家想要多理解的话点这里

快速排序 非递归https://blog.csdn.net/qq_41890240/article/details/124110735，这个大大写的非常详细，这里我就不细说啦！膜拜膜拜！

 

归并排序的递归： 

归并排序与之前练习过的合并两个有序数组相似，将两个有序数组合并为同一个有序数组，最终的有序数组为临时创建的数组，归并排序的前提条件是分开的左右两个数据有序，由于随机给的数据不太可能是左右两边都有序，此时我们就可以想到将左右两边的数组不断地分组，知道一个数据为一组，可以看成是有序的，不断拆分的过程就是不断递归的过程。

接下来的问题就是如何将左右两个有序数据合并为一个有序的数组。

从两个数组的第一个元素开始比较，把小的放在新数组的第一个位置上，小的数组索引++，再接着与另一个数组的第一个元素比较，仍是把小的放在新数组上，以此类推即可。

这里的难点是递归的理解，递归中止的条件是，数组被分成了只有一个数据的数组，即左右下标相同，一次递归结束后（左边）只有一个数据，会进入上一层递归进行下一步操作，即找到右边的一个数据，接着进行有序数组的合并，接着将在临时数组已经排好序的两个数据拷贝到原数组中即可。

代码如下：

//归并排序
void _MergeSort(int* a, int left, int right,int* tmp)
{
	if (left >= right)
		return;
	int mid = (left + right) >> 1;
	//假设[left,mid][mid+1，right]有序，就可以使用归并排序
	_MergeSort(a, left, mid, tmp);
	_MergeSort(a, mid + 1, right, tmp);
	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int index = left;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if(a[begin1]

归并排序的非递归算法：

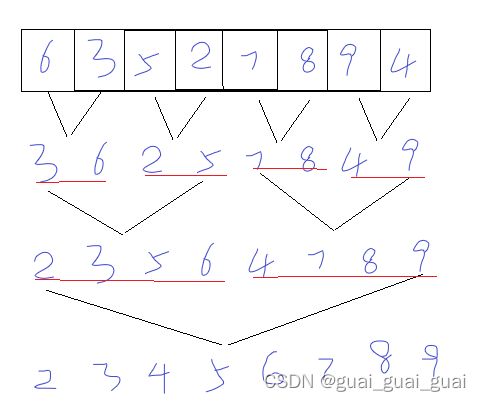
先设置一个gap为1，gap为要排序的每个数组（被分为若干份）的个数，以下图为例，将6和3看成一组，将其进行有序数组的排序，放在一个新数组中，后面的数依次排序并拷贝到新数组中，一轮排序完成后，将新数组的数拷贝到原数组中，接着将gap变为2，即3 6，5 2两个数组排序成2 3 5 6拷贝至新数组中，以此类推，，最终合并为一个1有序数组。

代码如下：

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			int index = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}
		}
		//拷贝
		for (int j = 0; j < n; j++)
		{
			a[j] = tmp[j];
		}
		gap *= 2;
	}
	free(tmp);
}

 里面对于两个有序数组合并为一个有序数组问题与归并排序思想相同，排序部分的代码也与递归相同，只是将递归变成循环而已。但是这个代码有一个缺陷，就是如果当数组个数为奇数，最终总会有一个不能像其他数据一样有与其相同个数的数组排序如下：

由于gap每次都*2，也有可能右半区间数据个数不够，因此需要适当修正一下。

 当然，左半区间也可能出现个数不够的情况，这时左半部分就不会进行排序，并不会拷贝到新数组中，这时将新数组中的数据拷贝到原数组最后几个左区间就会是随机值，因此将新数组的数据拷贝到原数组中时，需要将排过序的数组拷贝至原数组中。

//归并过程中右半区间可能不存在
if (begin2 >= n)
	break;
// 归并区间右半部分区间算多了，修正一下
if (end2 >= n)
	end2 = n - 1;

拷贝：

//拷贝
			for (int j = i; j < i + end2; j++)
			{
				a[j] = tmp[j];
			}

修改后的代码：

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			//归并过程中右半区间可能不存在
			if (begin2 >= n)
				break;
			// 归并区间右半部分区间算多了，修正一下
			if (end2 >= n)
				end2 = n - 1;
			int index = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}
			//拷贝
			for (int j = i; j <= end2; j++)
			{
				a[j] = tmp[j];
			}
		}
		
		
		gap *= 2;
	}
	free(tmp);
}

这样子无论数组元素个数为多少都可以排序成功啦！