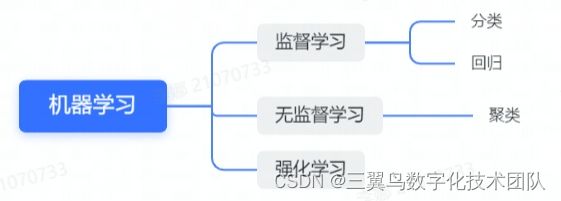
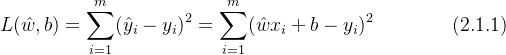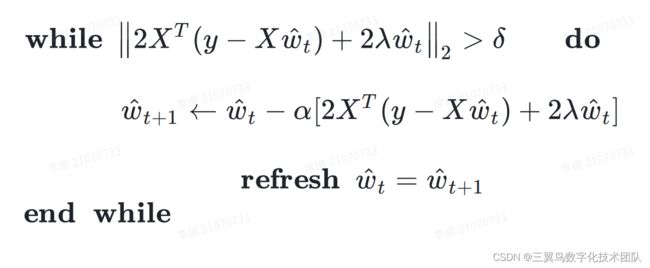三翼鸟数字化技术团队

监督学习之回归模型

1.术语解释

监督学习：利用一组有标签的样本数据训练和调优模型参数，使其达到所要求性能的过程。

分类模型：分类的输出为研究对象所属的类别，类别状态个数有限且离散，是一种定性分析。例如，天气晴、阴、雨三种类型，明天天气预测一定是属于这三种天气类型之一。

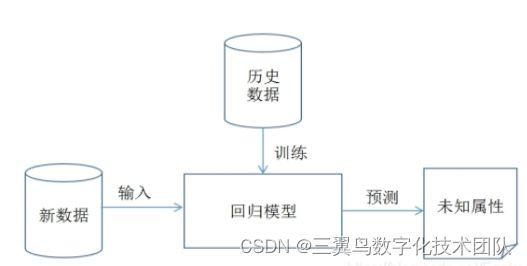
回归模型：回归所预测输出为连续的数值类型，属于一种定量分析。例如，回归模型用于预测明天降雨量具体是多少，是一个连续的变量。

2.回归模型

2.1 线性回归

线性回归假设因变量和自变量之间是线性的，表征了从输入变量到输出变量之间的线性映射关系，利用回归方程对一个或多个自变量和因变量之间关系进行建模的一种分析方式，数学形式。根据自变量的数目可划分为一元线性回归和多元线性回归。

应用场景：要求自变量和因变量是线性关系，如身高体重预测、工龄薪资预测、房价预测等。

2.1.1 一元线性回归实例

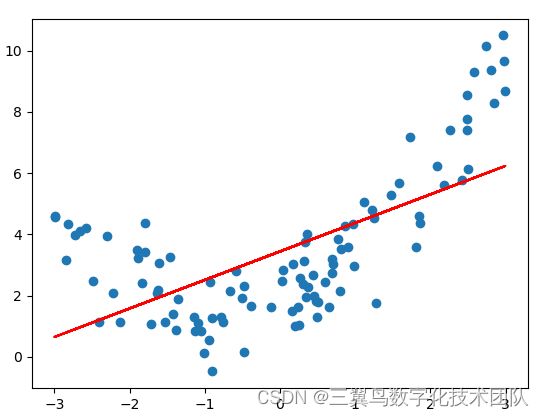
我们结合身高_体重曲线拟合案例，介绍一元线性回归的实际应用。本案例主要目的是根据身高和体重数据拟合一条最佳曲线，输入身高值就可以预测出体重。

本案例使用的数据集包括600个样本，部分数据如下

从表中可以获知该数据集包括三个标签，即“gender”，“height”，“weight”，其中“height”项作为自变量H（输入），“weight”为因变量W（输出），建立一元线性回归模型$$W=aH+b$$进行数据拟合，python实现过程如下：

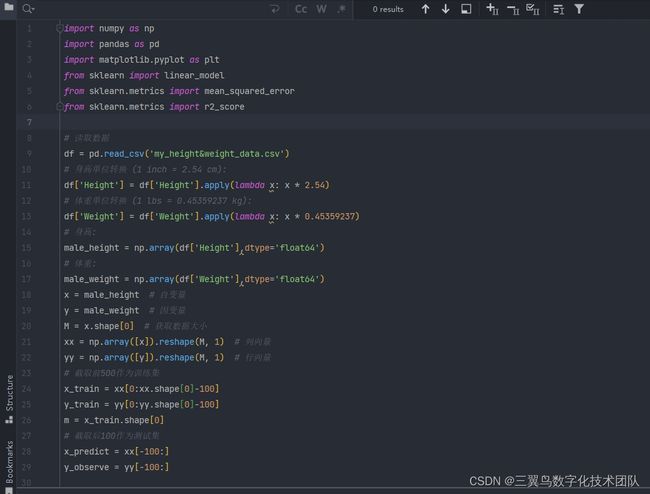
（1）首先，导入数据，500个样本作为训练集，其余100测试集用于验证

（2）使用sklearn提供的线性回归函数拟合数据，或者直接使用正规方程，求解模型参数a和b

(3) 输出结果：

所得线性回归方程为：

W=1.07H-102.10

2.1.2 多元线性回归实例

波士顿房地产市场竞争激烈，而你想成为该地区最好的房地产经纪人。为了更好地与同行竞争，你决定运用机器学习的一些基本概念，帮助客户为自己的房产定下最佳售价。幸运的是，你找到了波士顿房价的数据集，里面聚合了波士顿包含多个特征维度的房价数据。你的任务是用可用的工具进行统计分析，并基于分析建立优化模型，这个模型将用来为你的客户评估房产的最佳售价。

数据集如下图所示，本数据集共包含381条样本，每个样本包含13个特征维度，309个作为训练集，72个测试集

（1）利用多元线性回归模型对数据进行学习，并预测测试集数据。将CRIM, ZN, INDUS, CHAS, NOX, RM, AGE, DIS, RAD, TAX, PTRATIO, B, LSTAT这13个特征作为训练输入，MEDA特征看作输出，建立以下线性回归方程

$y=\theta_0x_{0}+\theta_1x_{1}+\cdots+\theta_{12}x_{12}+\theta_{13}$

其中 $\theta^T=(\theta_0,\theta_1,\cdots,\theta_{13})$ 为待学习的14个系数，这样波士顿房价问题就转化为一个多元线性回归问题。

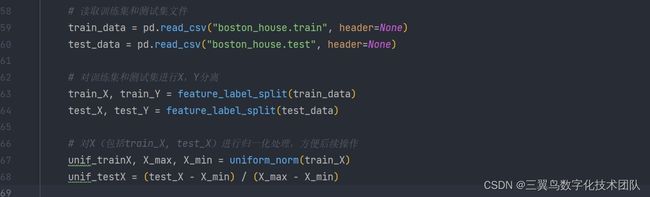
（2）老规矩，先上代码，导入数据集

（3）LinearRegression()进行模型训练，求解参考式(2.1.8)正规方程

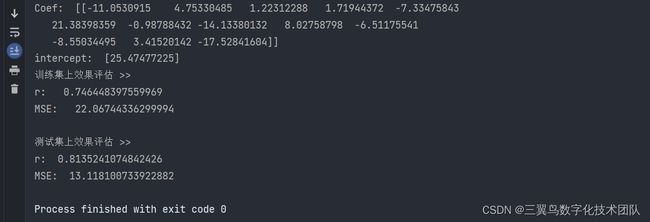
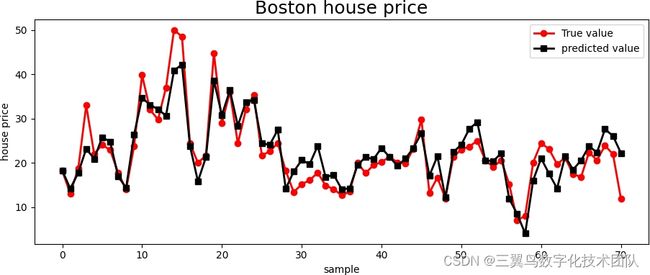
（4）结果分析

可知波士顿房价多元线性回归方程为

$y=-11.05x_0+4.75x_1+1.22x_2+1.72x_3-7.33x_4+21.38x_5-0.99x_6\\-14.13x_7+8.03x_8-6.51x_9-8.55x_{10}+3.42x_{11}-17.53x_{12}+25.47$

2.1.3 算法原理

A. 一元线性回归

给定一组由输入和输出构成的训练数据集 $D=\{(x_1, y_1), (x_2, y_2),\cdots,(x_m, y_m)\}$ ， $y_i\in R$ 线性回归就是通过该训练集训练得到一个线性模型来最大限度地根据输入拟合输出，使得 $y\cong \hat{y}=\hat{w}x+b$ 。因此，线性回归任务的关键在于确定参数 $\hat{w}$ 和，使得拟合输出 $\hat{y}$ 尽可能逼近真实输出，通常使用残差平方和函数来表示预测值与实际值之间的损失函数

$L(\hat{w}, b)= \displaystyle \sum_{i=1}^m (\hat{y}_i -y_i)^2 = \displaystyle\sum_{i=1}^m (\hat{w}x_i+b-y_i)^2 \qquad\qquad (2.1.1)$

为使损失函数值 $L(\hat{w}, b)$ 最小化，分别对 $\hat{w}$ 和求一阶偏导

$\begin{cases} \frac{\partial{L(\hat{w}, b)}}{\partial{\hat{w}}} = 2 [w \displaystyle\sum_{i=1}^m x_i^2 - \displaystyle\sum_{i=1}^m x_iy_i + b \displaystyle\sum_{i=1}^m x_i]\\ \frac{\partial{L(\hat{w}, b)}}{\partial{b}} =2 [mb - \displaystyle\sum_{i=1}^m (y_i - \hat{w}x_i)] \end{cases}\qquad\qquad (2.1.2)$

令上式 $\frac{\partial{L(\hat{w}, b)}}{\partial{\hat{w}}} = 0$ ， $\frac{\partial{L(\hat{w}, b)}}{\partial{b}} = 0$ ，可得到最优解析解 $\hat{w}^*$ 和代数式

$\begin{cases} \hat{w}^* = \frac{ \displaystyle\sum_{i=1}^m x_iy_i - \frac{1}{m}{\displaystyle\sum_{i=1}^m x_i} \displaystyle\sum_{i=1}^m y_i } {\displaystyle \sum_{i=1}^m x_i^2 - \frac{1}{m} (\displaystyle\sum_{i=1}^m x_i)^2} \\ b^* = \frac{1}{m} {\displaystyle \sum_{i=1}^m} {(y_i-\hat{w}^*x_i)} \end{cases}\qquad\qquad (2.1.3)$

B. 多元线性回归

一元线性回归研究的是目标变量和一个自变量之间的回归问题，但有时候在很多实际问题中，影响目标变量的自变量往往不止一个，而是多个，比如绵羊的产毛量这一变量同时受到绵羊体重、胸围、体长等多个变量共同影响，因此需要设计一个目标变量与多个自变量间的回归分析，即多元回归分析。

给定一组由输入和输出构成的多特征训练数据集 $D=\{(x_1, y_1), (x_2, y_2),\cdots,(x_m, y_m)\}$ ，其中 $x_i \in (x_{i1}; x_{i2}; \cdots; x_{id})$ ， $y_i\in R$ ，为输入的特征数量，多元线性回归一般方程为

$y_i=w_1x_{i1}+w_2x_{i2}+\cdots+w_dx_{id}+b \qquad\qquad (2.1.4)$

将参数向量与截距合并为向量表达形式， $\hat{w}=(w; b)=(w_1;w_2;\cdots;w_d;w_{d+1})$ 。此时训练集输入部分可表示为一个 $m \times (d+1)$ 维的矩阵：

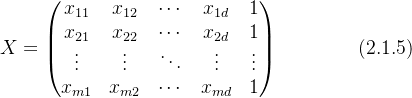
$X=\begin{pmatrix} x_{11}&x_{12}&\cdots&x_{1d} &1 \\ x_{21}&x_{22}&\cdots&x_{2d} &1 \\ \vdots&\vdots&\ddots&\vdots&\vdots \\ x_{m1}&x_{m2}&\cdots&x_{md} &1 \\ \end{pmatrix} \qquad\qquad (2.1.5)$

输出向量 $y=(y_{i1}; y_{i2}; \cdots; y_{id})$ ，可得损失函数矩阵形式

$L(\hat{w})=(y-X\hat{w})^T(y-X\hat{w})= {\begin{Vmatrix} y-X\hat{w} \end{Vmatrix}_2}^2 \qquad\qquad (2.1.6)$

对上式求偏导可得

$\frac {\partial L(\hat{w})} {\partial \hat{w}} =2X^T(X\hat{w}-y)=0 \qquad\qquad (2.1.7)$

该多元线性回归的正规方程解为

$\hat{w}^*=(X^TX)^{-1}X^Ty \qquad\qquad (2.1.8)$

求得多元线性回归方程点积形式为

$\hat{y}= \begin{pmatrix} x_{k1}&{x_{k2}}&\cdots&{x_{kd}}&1\\ \end{pmatrix} \cdot \begin{pmatrix} \hat{w}_1^*&\hat{w}_2^*&\cdots &\hat{w}_d^*&\hat{w}_{d+1}^*\\ \end{pmatrix}\\ \quad\\ = \hat{w}_1^*x_{k1} + \hat{w}_2^* x_{k2} + \cdots + \hat{w}_d^* {x_{kd}}+\hat{w}_{d+1}^* \qquad\qquad (2.1.9)$

①当数据量较小时，该方法求最优解是可行的，当数据量很大时，对矩阵求逆运算量极大，这就需要使用梯度下降方法或者牛顿迭代法逼近最优解；

②当为非满秩矩阵时，奇异阵的逆矩阵不存在，不能采用最小二乘法求解。

C. 梯度下降法

首先，计算代价函数 $J(\hat{w})= \frac{1}{2m} {\begin{Vmatrix} y-X\hat{w} \end{Vmatrix}_2}^2$ 的一阶梯度向量

$\nabla_{J(\hat{w})} = \frac{1}{m} \cdot X^T(X\hat{w}-y) \qquad\qquad (2.1.10)$

给定一个任意点 $\hat{w_0}=(w_1;w_2;\cdots;w_{d+1})$ ，设定步长(学习率) $\alpha \in [0, 1]$ ，容差 $\delta \rightarrow 0$ ，迭代下式

$\hat{w}_{t+1} \ \leftarrow \hat{w}_t - \alpha \nabla_{J(\hat{w}_t)} \qquad\qquad (2.1.11)$

直至满足 ${\begin{Vmatrix} \nabla_{J(\hat{w}_t)} \end{Vmatrix}_2} < \delta$ ，此时总梯度趋近于0，说明在函数在 $\hat{w}_t$ 处取最小值。

2.2 Ridge回归

Ridge回归可以看作是线性回归的改进算法，Ridge回归通过L2正则化项来改进损失函数，以增强回归算法的鲁棒性。以房价估计为例，在影响房价的众多因素中，会存在一些对房价影响基本可以忽略不计的因素，如何从众多因素中找到关键影响因素，对无关紧要的因素进行权重压缩是一个值得考虑的问题。由式(2.1.8)可知线性回归的最优参数估计为 $\hat{w}^*=(X^TX)^{-1}X^Ty$ ，当训练样本的特征数大于样本数量时，矩阵非满秩，不可逆，所以 $\hat{w}^*$ 是不可估计的。

2.2.1 应用实例

序号	price	bedrooms	bathrooms	living_sqrt	floors
0	545000	3	2.25	1670	1
1	765000	4	2.5	3300	2
2	720000	3	3.25	3190	2

以二手房房价估计问题为例，我们使用Ridge回归来解决该回归问题，本案例的输入为卧室数量(bedrooms)、卫生间数量(bathrooms)、居住面积(living_sqrt)和楼层(floors)4个特征，输出为房子的价格。

目前我们手中只有三个样本作为训练数据，此时样本数量(3)<特征数(4)，为奇异矩阵，故使用线性回归求解是不可行的。此时我们可以使用Ridge回归算法来解决该问题，根据式(2.2.3)正规方程中的输入项，对训练数据进行整理，可得

代入式(2.2.3)得该Ridge回归房价数学模型为

$\hat{y}= 79161x_0+56801x_1+84x_2-1739x_3+33689$

2.2.2 算法原理

Ridge回归(岭回归)在线性回归损失函数(2.1.6)中加入一个L2正则化项来改造损失函数模型

$L(\hat{w})= (y-X\hat{w})^T(y-X\hat{w}) +\lambda {\begin{Vmatrix} \hat{w} \end{Vmatrix}_2}^2 \qquad\qquad (2.2.1)$

$\lambda$ 为正则化系数，二范数为惩罚项。通过采用有偏估计，以舍弃一部分信息与精度为代价，从而使得函数模型更加可靠，模型与病态数据的拟合性更好。更有趣的是，相比L1范数(Lasso回归)，式(2.2.1)中的L2范数正则化项是连续可微的，即可以通过函数的一阶梯度向量求得最优解

$\nabla_{\hat{w}}{L(\hat{w})} = 2X^T(y-X\hat{w})+2\lambda \hat{w} \qquad\qquad (2.2.2)$

令上式 $\frac{\partial}{\partial \hat{w}}L(\hat{w})=0$ ，最优解矩阵形式为

$\hat{w}^*=(X^TX+\lambda E)^{-1}X^Ty \qquad\qquad\qquad\qquad (2.2.3)$

其中为单位阵。当数据量较大时，同样也可以使用梯度下降方法求解

2.3 多项式回归

线性回归和Ridge回归的局限性是只能应用于存在严格线性关系的数据中，但是在实际生活中，很多数据之间是非线性关系，虽然也可以用线性回归拟合非线性回归，但是效果会变差，这时候就需要对线性回归模型进行改进，使之能够拟合非线性数据。

多项式回归研究因变量与一个或多个自变量间多项式的回归分析方法。如果自变量只有一个时，称为一元多项式回归，数学定义为 $y= \theta_0 + \theta_1x+ \theta_2x^2+ \cdots + \theta_nx^n$ ；如果自变量有多个时，称为多元多项式回归。多项式回归相对于其他的回归分析方法有一个很大的优点，它可以依次增加多项式的次数，这样一步一步地对观测点进行逼近通过观察模拟效果和误差分析以至达到最好的效果。

应用场景：数据存在非线性关系

2.3.1 一元二阶多项式回归实例

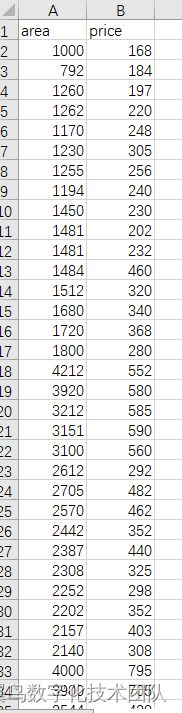
一元二阶多项式，简单说即。我们有一批关于房屋建筑面积和成交价格的数据集，我们需要做的是采用合适的方法拟合这些数据得到一个模型，通过该模型输入一个任意 area可以预测到 price。数据集如下表，信息包括房屋的面积 area 以及对应的成交价格 price 两个属性，由此可推断该问题是一个一元回归问题，一元回归方法包括线性回归或多项式回归，但究竟应该使用哪一种方案对房屋价格进行预测更加适合呢？

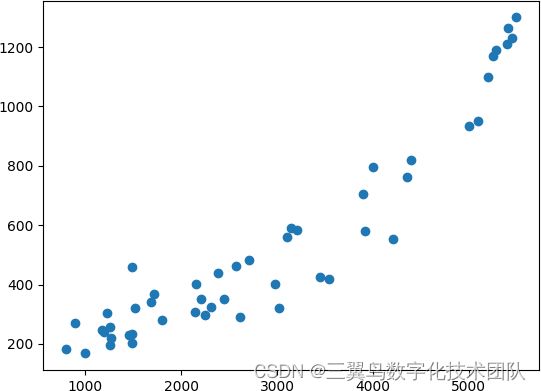
（1）首先，我们可以根据数据散点图的特点观察判断数据是线性或非线性，再选择最佳的回归方法。画出上表中数据散点分布图如下图所示，可以看出该图具有抛物线特征，故我们选取一元二次多项式拟合方法，即

其中代表房屋面积，为价格，是待学习参数。从本质上看，本例中多项式回归将原本只有一个特征维度的数据集拓展成一个二维度数据集，和，具有升维作用。

（2）数据预处理，数据分割

（3）建立一元二次多项式，使用线性回归模型对参数进行训练

（4）结果显示

所求二次多项式回归方程为

2.3.2 算法原理

A. 一元多项式回归

在一元回归分析中，如果数据 $(x_i,y_i),i=1,2,\cdots,m$ 的关系为非线性的，此时使用线性回归找不到理想的线性函数对曲线进行拟合，可以采用一元多项式回归，一元阶多项式回归方程如下

$\hat{y}_i= \hat{w}_0 + \hat{w}_1x_i+ \hat{w}_2x_i^2 + \cdots + \hat{w}_dx_i^d \qquad\qquad\qquad (2.3.1)$

通过变量转换办法，令 $t_{i1}=x_i,t_{i2}=x_i^2,\cdots,t_{id}=x_i^d$ ，此时可以将式(2.3.1)变形得到一个元线性回归方程

$\hat{y}_i= \hat{w}_0 + \hat{w}_1t_{i1}+ \hat{w}_2t_{i2 }+ \cdots + \hat{w}_dt_{id} \qquad\qquad\qquad (2.3.2)$

写成矩阵表达形式为

由2.1部分数学推导可知线性回归正规方程解为

$\hat{w}^*=(T^TT)^{-1}T^Ty \qquad\qquad (2.3.4)$

其中

$T= \begin{pmatrix} 1&t_{11}&t_{12}&\cdots&t_{1d}\\ 1&t_{21}&t_{22}&\cdots&t_{2d}\\ \vdots&\vdots&\ddots&\vdots&\vdots \\ 1&t_{m1}&t_{m2}&\cdots&t_{md}\\ \end{pmatrix} = \begin{pmatrix} 1&x_1&x_1^2&\cdots&x_1^d\\ 1&x_2&x_2^2&\cdots&x_2^d\\ \vdots&\vdots&\ddots&\vdots&\vdots \\ 1&x_m&x_m^2&\cdots&x_m^d\\ \end{pmatrix}, y= \begin{pmatrix} y_1\\ y_2\\ \vdots\\ y_m \end{pmatrix}$

所求一元阶多项式回归方程为

$\hat{y}= \begin{pmatrix} 1&x&{x}^2&\cdots&{x}^d\\ \end{pmatrix} \cdot \begin{pmatrix} \hat{w}_0^*&\hat{w}_1^*&\hat{w}_2^*&\cdots&\hat{w}_d^*\\ \end{pmatrix}\\ \quad\\ = \hat{w}_0^* + \hat{w}_1^* x+ \hat{w}_2^* {x}^2 + \cdots + \hat{w}_d^* {x}^d \qquad\qquad (2.3.5)$

B. 多元多项式回归

当一个非线性数据集包含两个及两个以上特征变量时，该问题变成多元多项式回归问题。我们以简单的二元二阶多项式为例，考虑训练数据集 $D=\{(x_1, y_1), (x_2, y_2),\cdots,(x_m, y_m)\}$ ，其中 $x_i \in (x_{i1}; x_{i2})$ ， $y_i\in R$ ，其回归方程定义如下

$\hat{y_i} = \hat{w}_0+ \hat{w}_1x_{i1}+ \hat{w}_2x_{i2}+ \hat{w}_3x_{i1}x_{i2}+ \hat{w}_4x_{i1}^2+ \hat{w}_5x_{i2}^2 \qquad\qquad (2.3.6)$

同理，式(2.3.6)可变换为多元线性回归模型

$\hat{y_i} = \hat{w}_0+ \hat{w}_1t_{i1}+ \hat{w}_2t_{i2}+ \hat{w}_3t_{i3}+ \hat{w}_4t_{i4}+ \hat{w}_5t_{i5} \qquad\qquad (2.3.7)$

其中 $t_{i1}=x_{i1},t_{i2}=x_{i2},t_{i3}=x_{i1}x_{i2},t_{i4}=x_{i1}^2,t_{i5}=x_{i2}^2$ 。

因此可知其最优解为

$\hat{w}^*=(T^TT)^{-1}T^Ty \qquad\qquad\qquad (2.3.8)$

其中

$T= \begin{pmatrix} 1&t_{11}&t_{12}&t_{13}&t_{14}&t_{15}\\ 1&t_{21}&t_{22}&t_{23}&t_{24}&t_{25}\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots \\ 1&t_{m1}&t_{m2}&t_{m3}&t_{m4}&t_{m5}\\ \end{pmatrix} = \begin{pmatrix} 1&x_{11}&x_{12}&x_{11}x_{12}&x_{11}^2&x_{12}^2\\ 1&x_{21}&x_{22}&x_{21}x_{22}&x_{21}^2&x_{22}^2\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots \\ 1&x_{m1}&x_{m2}&x_{m1}x_{m2}&x_{m1}^2&x_{m2}^2\\ \end{pmatrix}$

该二元二阶多项式回归方程向量内积形式为

$\hat{y}= \begin{pmatrix} 1&x_{k1}&{x_{ k2}}&x_{k1}x_{k2}&x_{k1}^2&x_{k2}^2\\ \end{pmatrix} \cdot \begin{pmatrix} \hat{w}_0^*&\hat{w}_1^*&\hat{w}_2^*&\hat{w}_3^*&\hat{w}_4^*&\hat{w}_5^*\\ \end{pmatrix}\\ \quad\\ = \hat{w}_0^* + \hat{w}_1^* x_{k1}+ \hat{w}_2^* x_{k2} + \hat{w}_3^*x_{k1}x_{k2} + \hat{w}_4^* x_{k1}^2 + \hat{w}_5^* x_{k2}^2 \qquad\quad (2.3.9)$

虽然多项式回归使用可能达到比线性回归更好的效果，但需要注意过拟合效应。

小结

	假设形式	损失函数	适用场景
线性回归		$L=(y-X\hat{w})^T(y-X\hat{w})$	线性数据，特征数小于数据容量
Ridge回归		$L=(y-X\hat{w})^T(y-X\hat{w}) +\lambda {\begin{Vmatrix} \hat{w} \end{Vmatrix}_2}^2$	线性数据，数据特征数量大，需要压缩，数据存在多重线性关系
多项式回归		$L=(y-X\hat{w})^T(y-X\hat{w})$	非线性数据

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
理解Gunicorn：Python WSGI服务器的基石范范0825 ipython linux 运维
理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
Python数据分析与可视化实战指南 William数据分析 python python 数据
在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
python os.environ 江湖偌大 python 深度学习
os.environ['TF_CPP_MIN_LOG_LEVEL']='0'#默认值，输出所有信息os.environ['TF_CPP_MIN_LOG_LEVEL']='1'#屏蔽通知信息（INFO）os.environ['TF_CPP_MIN_LOG_LEVEL']='2'#屏蔽通知信息和警告信息（INFO\WARNING）os.environ['TF_CPP_MIN_LOG_LEVEL']='
Python中os.environ基本介绍及使用方法鹤冲天Pro #Python python 服务器开发语言
文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
Pyecharts数据可视化大屏：打造沉浸式数据分析体验我的运维人生信息可视化数据分析数据挖掘运维开发技术共享
Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
Python教程：一文了解使用Python处理XPath 旦莫 Python进阶 python 开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
python os.environ_python os.environ 读取和设置环境变量 weixin_39605414 python os.environ
>>>importos>>>os.environ.keys()['LC_NUMERIC','GOPATH','GOROOT','GOBIN','LESSOPEN','SSH_CLIENT','LOGNAME','USER','HOME','LC_PAPER','PATH','DISPLAY','LANG','TERM','SHELL','J2REDIR','LC_MONETARY','QT_QPA
高端密码学院笔记285 柚子_b4b4
高端幸福密码学院（高级班）幸福使者：李华第（598）期《幸福》之回归内在深层生命原动力基础篇——揭秘“激励”成长的喜悦心理案例分析主讲：刘莉一，知识扩充:成功=艰苦劳动+正确方法+少说空话。贪图省力的船夫，目标永远下游。智者的梦再美，也不如愚人实干的脚印。幸福早课堂2020.10.16星期五一笔记:1，重视和珍惜的前提是知道它的价值非常重要，当你珍惜了，你就真正定下来，真正的学到身上。2，大家需要
使用Faiss进行高效相似度搜索 llzwxh888 faiss python
在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
python是什么意思中文-在python中%是什么意思编程大乐趣
Python中%有两种：1、数值运算：%代表取模，返回除法的余数。如：>>>7%212、%操作符（字符串格式化，stringformatting），说明如下：%[(name)][flags][width].[precision]typecode(name)为命名flags可以有+，-，''或0。+表示右对齐。-表示左对齐。''为一个空格，表示在正数的左侧填充一个空格，从而与负数对齐。0表示使用0填
Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Python python 开发语言大数据数据分析数据挖掘
大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
python八股文面试题分享及解析(1) Shawn________ python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果：21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型，不仅仅改变
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
Python快速入门 —— 第三节：类与对象孤华暗香 Python快速入门 python 开发语言
第三节：类与对象目标：了解面向对象编程的基础概念，并学会如何定义类和创建对象。内容：类与对象：定义类：class关键字。类的构造函数：__init__()。类的属性和方法。对象的创建与使用。示例：classStudent:def__init__(self,name,age,major):self.name&#
pyecharts——绘制柱形图折线图 2224070247 信息可视化 python java 数据可视化
一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd）数据可视化团队研发的ECharts1.0发布到GitHub网站以来，ECharts一直备受业界权威的关注并获得广泛好评，成为目前成熟且流行的数据可视化图表工具，被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言，也加入ECharts的使用行列，并研发出方便Python开发者使用的数据
Python 实现图片裁剪（附代码） | Python工具剑客阿良_ALiang
前言本文提供将图片按照自定义尺寸进行裁剪的工具方法，一如既往的实用主义。环境依赖ffmpeg环境安装，可以参考我的另一篇文章：windowsffmpeg安装部署_阿良的博客-CSDN博客本文主要使用到的不是ffmpeg，而是ffprobe也在上面这篇文章中的zip包中。ffmpy安装：pipinstallffmpy-ihttps://pypi.douban.com/simple代码不废话了，上代码
【华为OD技术面试真题 - 技术面】- python八股文真题题库（4) 算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例：文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片（Slicing）操作**基本切片语法
python os 环境变量 CV矿工 python 开发语言 numpy
环境变量：环境变量是程序和操作系统之间的通信方式。有些字符不宜明文写进代码里，比如数据库密码，个人账户密码，如果写进自己本机的环境变量里，程序用的时候通过os.environ.get（）取出来就行了。os.environ是一个环境变量的字典。环境变量的相关操作importos"""设置/修改环境变量：os.environ[‘环境变量名称’]=‘环境变量值’#其中key和value均为string类
Python爬虫解析工具之xpath使用详解 eqa11 python 爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中，数据提取是一个至关重要的环节。xpath作为一门
【华为OD技术面试真题 - 技术面】- python八股文真题题库（1）算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.数据预处理流程数据预处理的主要步骤工具和库2.介绍线性回归、逻辑回归模型线性回归（LinearRegression）模型形式：关键点：逻辑回归（LogisticRegression）模型形式：关键点：参数估计与评估：3.python浅拷贝及深拷贝浅拷贝（Shal
数字里的世界17期：2021年全球10大顶级数据中心，中国移动榜首张三叨
你知道吗？2016年，全球的数据中心共计用电4160亿千瓦时，比整个英国的发电量还多40％！前言每天，我们都会创造超过250万TB的数据。并且随着物联网（IOT）的不断普及，这一数据将持续增长。如此庞大的数据被存储在被称为“数据中心”的专用设施中。虽然最早的数据中心建于20世纪40年代，但直到1997-2000年的互联网泡沫期间才逐渐成为主流。当前人类的技术，比如人工智能和机器学习，已经将我们推向
nosql数据库技术与应用知识点皆过客，揽星河 NoSQL nosql 数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
《Python数据分析实战终极指南》 xjt921122 python 数据分析开发语言
对于分析师来说，大家在学习Python数据分析的路上，多多少少都遇到过很多大坑**，有关于技能和思维的**：Excel已经没办法处理现有的数据量了，应该学Python吗？找了一大堆Python和Pandas的资料来学习，为什么自己动手就懵了？跟着比赛类公开数据分析案例练了很久，为什么当自己面对数据需求还是只会数据处理而没有分析思路？学了对比、细分、聚类分析，也会用PEST、波特五力这类分析法，为啥
Python中深拷贝与浅拷贝的区别 yuxiaoyu.
转自：http://blog.csdn.net/u014745194/article/details/70271868定义：在Python中对象的赋值其实就是对象的引用。当创建一个对象，把它赋值给另一个变量的时候，python并没有拷贝这个对象，只是拷贝了这个对象的引用而已。浅拷贝：拷贝了最外围的对象本身，内部的元素都只是拷贝了一个引用而已。也就是，把对象复制一遍，但是该对象中引用的其他对象我不复
Python开发常用的三方模块如下：换个网名有点难 python 开发语言
Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
Python编译器鹿鹿~ Python编译器 Python python 开发语言后端
嘿嘿嘿我又来了啊有些小盆友可能不知道Python其实是有编译器的，也就是PyCharm。你们可能会问到这个是干嘛的又不可以吃也不可以穿好像没有什么用，其实你还说对了这个还真的不可以吃也不可以穿，但是它用来干嘛的呢。用来编译你所打出的代码进行运行（可能这里说的有点不对但是只是个人认为）现在我们来说说PyCharm是用来干嘛的。PyCharm是一种PythonIDE，带有一整套可以帮助用户在使用Pyt
一文掌握python面向对象魔术方法（二）程序员neil python python 开发语言
接上篇：一文掌握python面向对象魔术方法（一）-CSDN博客目录六、迭代和序列化：1、__iter__(self):定义迭代器，使得类可以被for循环迭代。2、__getitem__(self,key):定义索引操作，如obj[key]。3、__setitem__(self,key,value):定义赋值操作，如obj[key]=value。4、__delitem__(self,key):定义
一文掌握python常用的list（列表）操作程序员neil python python 开发语言
目录一、创建列表1.直接创建列表：2.使用list()构造器3.使用列表推导式4.创建空列表二、访问列表元素1.列表支持通过索引访问元素，索引从0开始：2.还可以使用切片操作访问列表的一部分：三、修改列表元素四、添加元素1.append()：在末尾添加元素2.insert()：在指定位置插入元素五、删除元素1.del：删除指定位置的元素2.remove()：删除指定值的第一个匹配项3.pop()：
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
java Illegal overloaded getter method with ambiguous type for propert的解决 zwllxs java jdk
好久不来iteye,今天又来看看，哈哈,今天碰到在编码时，反射中会抛出 Illegal overloaded getter method with ambiguous type for propert这么个东东，从字面意思看，是反射在获取getter时迷惑了，然后回想起java在boolean值在生成getter时，分别有is和getter，也许我们的反射对象中就有is开头的方法迷惑了jdk，
IT人应当知道的10个行业小内幕 beijingjava 工作互联网
10. 虽然IT业的薪酬比其他很多行业要好，但有公司因此视你为其“佣人”。　　尽管IT人士的薪水没有互联网泡沫之前要好，但和其他行业人士比较，IT人的薪资还算好点。在接下的几十年中，科技在商业和社会发展中所占分量会一直增加，所以我们完全有理由相信，IT专业人才的需求量也不会减少。　　然而，正因为IT人士的薪水普遍较高，所以有些公司认为给了你这么多钱，就把你看成是公司的“佣人”，拥有你的支配
java 实现自定义链表 CrazyMizzz java 数据结构
1.链表结构链表是链式的结构 2.链表的组成链表是由头节点，中间节点和尾节点组成节点是由两个部分组成： 1.数据域 2.引用域 3.链表的实现 &nbs
web项目发布到服务器后图片过一会儿消失麦田的设计者 struts2 上传图片永久保存
作为一名学习了android和j2ee的程序员，我们必须要意识到，客服端和服务器端的交互是很有必要的，比如你用eclipse写了一个web工程，并且发布到了服务器（tomcat）上，这时你在webapps目录下看到了你发布的web工程，你可以打开电脑的浏览器输入http://localhost:8080/工程/路径访问里面的资源。但是，有时你会突然的发现之前用struts2上传的图片
CodeIgniter框架Cart类 name 不能设置中文的解决方法 IT独行者 CodeIgniter Cart 框架　
今天试用了一下CodeIgniter的Cart类时遇到了个小问题，发现当name的值为中文时，就写入不了session。在这里特别提醒一下。在CI手册里也有说明，如下： $data = array( 'id' => 'sku_123ABC', 'qty' => 1, '
linux回收站 _wy_ linux 回收站
今天一不小心在ubuntu下把一个文件移动到了回收站，我并不想删，手误了。我急忙到Nautilus下的回收站中准备恢复它，但是里面居然什么都没有。后来我发现这是由于我删文件的地方不在HOME所在的分区，而是在另一个独立的Linux分区下，这是我专门用于开发的分区。而我删除的东东在分区根目录下的.Trash-1000/file目录下，相关的删除信息（删除时间和文件所在
jquery回到页面顶端知了ing html jquery css
html代码： <h1 id="anchor">页面标题</h1> <div id="container">页面内容</div> <p><a href="#anchor" class="topLink">回到顶端</a><
B树、B-树、B+树、B*树矮蛋蛋 B树
原文地址： http://www.cnblogs.com/oldhorse/archive/2009/11/16/1604009.html B树即二叉搜索树： 1.所有非叶子结点至多拥有两个儿子（Left和Right）； &nb
数据库连接池 alafqq 数据库连接池
http://www.cnblogs.com/xdp-gacl/p/4002804.html @Anthor:孤傲苍狼数据库连接池用MySQLv5版本的数据库驱动没有问题，使用MySQLv6和Oracle的数据库驱动时候报如下错误： java.lang.ClassCastException: $Proxy0 cannot be cast to java.sql.Connec
java泛型百合不是茶 java泛型
泛型在Java SE 1.5之前，没有泛型的情况的下，通过对类型Object的引用来实现参数的“任意化”，任意化的缺点就是要实行强制转换，这种强制转换可能会带来不安全的隐患泛型的特点：消除强制转换确保类型安全向后兼容简单泛型的定义：泛型：就是在类中将其模糊化，在创建对象的时候再具体定义 class fan
javascript闭包[两个小测试例子] bijian1013 JavaScript JavaScript
一.程序一 <script> var name = "The Window"; var Object_a = { 　　name : "My Object", 　　getNameFunc : function(){ var that = this; 　　　　return function(){ 　　　　
探索JUnit4扩展：假设机制（Assumption） bijian1013 java Assumption JUnit 单元测试
一.假设机制（Assumption）概述理想情况下，写测试用例的开发人员可以明确的知道所有导致他们所写的测试用例不通过的地方，但是有的时候，这些导致测试用例不通过的地方并不是很容易的被发现，可能隐藏得很深，从而导致开发人员在写测试用例时很难预测到这些因素，而且往往这些因素并不是开发人员当初设计测试用例时真正目的，
【Gson四】范型POJO的反序列化 bit1129 POJO
在下面这个例子中，POJO(Data类)是一个范型类，在Tests中，指定范型类为PieceData，POJO初始化完成后，通过 String str = new Gson().toJson(data); 得到范型化的POJO序列化得到的JSON串，然后将这个JSON串反序列化为POJO import com.google.gson.Gson; import java.
【Spark八十五】Spark Streaming分析结果落地到MySQL bit1129 Stream
几点总结： 1. DStream.foreachRDD是一个Output Operation，类似于RDD的action，会触发Job的提交。DStream.foreachRDD是数据落地很常用的方法 2. 获取MySQL Connection的操作应该放在foreachRDD的参数（是一个RDD[T]=>Unit的函数类型)，这样，当foreachRDD方法在每个Worker上执行时，
NGINX + LUA实现复杂的控制 ronin47 nginx lua
安装lua_nginx_module 模块 lua_nginx_module 可以一步步的安装，也可以直接用淘宝的OpenResty Centos和debian的安装就简单了。。这里说下freebsd的安装： fetch http://www.lua.org/ftp/lua-5.1.4.tar.gz tar zxvf lua-5.1.4.tar.gz cd lua-5.1.4 ma
java-递归判断数组是否升序 bylijinnan java
public class IsAccendListRecursive { /*递归判断数组是否升序 * if a Integer array is ascending,return true * use recursion */ public static void main(String[] args){ IsAccendListRecursiv
Netty源码学习-DefaultChannelPipeline2 bylijinnan java netty
Netty3的API http://docs.jboss.org/netty/3.2/api/org/jboss/netty/channel/ChannelPipeline.html 里面提到ChannelPipeline的一个“pitfall”：如果ChannelPipeline只有一个handler（假设为handlerA）且希望用另一handler（假设为handlerB）来
Java工具之JPS chinrui java
JPS使用熟悉Linux的朋友们都知道，Linux下有一个常用的命令叫做ps（Process Status)，是用来查看Linux环境下进程信息的。同样的，在Java Virtual Machine里面也提供了类似的工具供广大Java开发人员使用，它就是jps（Java Process Status)，它可以用来
window.print分页打印 ctrain window
function init() { var tt = document.getElementById("tt"); var childNodes = tt.childNodes[0].childNodes; var level = 0; for (var i = 0; i < childNodes.length; i++) {
安装hadoop时执行jps命令Error occurred during initialization of VM daizj jdk hadoop jps
在安装hadoop时，执行JPS出现下面错误 [slave16][email protected]:/tmp/hsperfdata_hdfs# jps Error occurred during initialization of VM java.lang.Error: Properties init: Could not determine current working
PHP开发大型项目的一点经验 dcj3sjt126com PHP 重构
一、变量最好是把所有的变量存储在一个数组中，这样在程序的开发中可以带来很多的方便，特别是当程序很大的时候。变量的命名就当适合自己的习惯，不管是用拼音还是英语，至少应当有一定的意义，以便适合记忆。变量的命名尽量规范化，不要与PHP中的关键字相冲突。二、函数 PHP自带了很多函数，这给我们程序的编写带来了很多的方便。当然，在大型程序中我们往往自己要定义许多个函数，几十
android笔记之--向网络发送GET/POST请求参数 dcj3sjt126com android
使用GET方法发送请求 private static boolean sendGETRequest (String path, Map<String, String> params) throws Exception{ //发送地http://192.168.100.91:8080/videoServi
linux复习笔记之bash shell (3) 通配符 eksliang linux 通配符 linux通配符
转载请出自出处： http://eksliang.iteye.com/blog/2104387 在bash的操作环境中有一个非常有用的功能，那就是通配符。下面列出一些常用的通配符，如下表所示符号意义 * 万用字符，代表0个到无穷个任意字符 ? 万用字符，代表一定有一个任意字符 [] 代表一定有一个在中括号内的字符。例如：[abcd]代表一定有一个字符，可能是a、b、c
Android关于短信加密 gqdy365 android
关于Android短信加密功能，我初步了解的如下（只在Android应用层试验）： 1、因为Android有短信收发接口，可以调用接口完成短信收发；发送过程：APP（基于短信应用修改）接受用户输入号码、内容——>APP对短信内容加密——>调用短信发送方法Sm
asp.net在网站根目录下创建文件夹 hvt .net C#hovertree asp.net Web Forms
假设要在asp.net网站的根目录下建立文件夹hovertree,C#代码如下： string m_keleyiFolderName = Server.MapPath("/hovertree"); if (Directory.Exists(m_keleyiFolderName)) { //文件夹已经存在 return; } else { try { D
一个合格的程序员应该读过哪些书 justjavac 程序员书籍
编者按：2008年8月4日，StackOverflow 网友 Bert F 发帖提问：哪本最具影响力的书，是每个程序员都应该读的？ “如果能时光倒流，回到过去，作为一个开发人员，你可以告诉自己在职业生涯初期应该读一本，你会选择哪本书呢？我希望这个书单列表内容丰富，可以涵盖很多东西。” 很多程序员响应，他们在推荐时也写下自己的评语。以前就有国内网友介绍这个程序员书单，不过都是推荐数
单实例实践跑龙套_az 单例
1、内部类 public class Singleton { private static class SingletonHolder { public static Singleton singleton = new Singleton(); } public Singleton getRes
PO VO BEAN 理解 q137681467 VO DTO po
PO：全称是 persistant object持久对象最形象的理解就是一个PO就是数据库中的一条记录。好处是可以把一条记录作为一个对象处理，可以方便的转为其它对象。 BO：全称是 business object:业务对象主要作用是把业务逻辑封装为一个对象。这个对
战胜惰性，暗自努力金笛子努力
偶然看到一句很贴近生活的话：“别人都在你看不到的地方暗自努力，在你看得到的地方，他们也和你一样显得吊儿郎当，和你一样会抱怨，而只有你自己相信这些都是真的，最后也只有你一人继续不思进取。”很多句子总在不经意中就会戳中一部分人的软肋，我想我们每个人的周围总是有那么些表现得“吊儿郎当”的存在，是否你就真的相信他们如此不思进取，而开始放松了对自己的要求随波逐流呢？我有个朋友是搞技术的，平时嘻嘻哈哈，以
NDK/JNI二维数组多维数组传递 wenzongliang 二维数组 jni NDK
多维数组和对象数组一样处理，例如二维数组里的每个元素还是一个数组用jArray表示，直到数组变为一维的，且里面元素为基本类型，去获得一维数组指针。给大家提供个例子。已经测试通过。 Java_cn_wzl_FiveChessView_checkWin( JNIEnv* env,jobject thiz,jobjectArray qizidata) { jint i,j; int s