pytorch-- 多维特征处理

目录

 接下来是我对于一些地方的理解，不正确希望大佬们指正

1 . 全连接层的设置

根据这个说法我增加了一层全连接层进行测试

2. 激活函数self.sigmiod = nn.Sigmoid()

这是比较理论的原因， 另一个原因 是我觉得非常重要的：

3.数据集的获取

---

import torch.nn as nn
import numpy as np
import torch

import matplotlib.pyplot as plt


xy = np.loadtxt('diabetes.csv', delimiter=',', dtype=np.float32, skiprows=1)
x_data = torch.from_numpy(xy[:, :-1])
y_data = torch.from_numpy(xy[:, [-1]])
epoch_list = []
loss_list = []
class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = nn.Linear(8, 6)
        self.linear2 = nn.Linear(6, 4)
        self.linear3 = nn.Linear(4, 1)
        self.sigmiod = nn.Sigmoid()

    def forward(self, x):
        x = self.sigmiod(self.linear1(x))
        x = self.sigmiod(self.linear2(x))
        x = self.sigmiod(self.linear3(x))

        return x

model = Model()
criterion = nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(), lr=1.0)


for epoch in range(100):
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    loss_list.append(loss.item())
    epoch_list.append(epoch)
    print(epoch, loss.item())
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()



plt.plot(loss_list,epoch_list, ls = '-.',c ='red')

plt.show()

 接下来是我对于一些地方的理解，不正确希望大佬们指正

1 . 全连接层的设置

self.linear1 = nn.Linear(8, 6)
self.linear2 = nn.Linear(6, 4)
self.linear3 = nn.Linear(4, 1) 

这三行代码是在定义模型的三个全连接层，每个层都有一个输入维度和一个输出维度。全连接层的作用是将输入的特征向量映射到一个新的空间，从而提取更高层次的特征。这里的维度选择是根据数据集的特点和模型的复杂度来确定的，一般来说，输出维度越小，模型越简单，但也可能损失一些信息。输入维度越大，模型越复杂，但也可能导致过拟合。 

形象点来说的话：

假设你要预测一个人是否患有糖尿病，你有八个输入特征，比如年龄、体重、血压等，你的输出是一个二分类的标签，0表示没有糖尿病，1表示有糖尿病。如果你只用一个全连接层（8，1），那么你的模型相当于一个线性回归模型，它只能找到输入特征和输出标签之间的线性关系，比如说年龄越大，患糖尿病的概率越高。但是这样的模型可能无法捕捉到更复杂的非线性关系，比如说体重和血压之间的交互作用，或者某些特征的非线性变换。这样的模型可能会在训练数据上表现不好，也就是欠拟合。

如果你用多个全连接层和Sigmoid激活函数，那么你的模型相当于一个逻辑回归模型，它可以找到输入特征和输出标签之间的非线性关系，比如说年龄和体重的乘积，或者血压的平方根等。这样的模型可以更好地拟合训练数据，也就是减少欠拟合。但是如果你用太多的全连接层和节点，那么你的模型可能会过度拟合训练数据，也就是忽略了噪声和泛化能力。所以你需要在模型复杂度和数据复杂度之间找到一个平衡点。

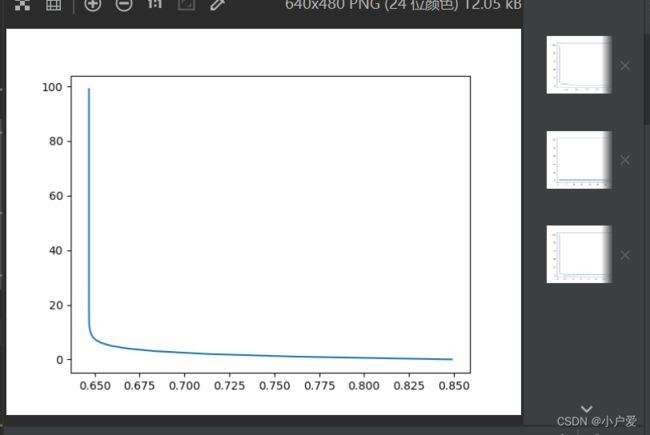
根据这个说法我增加了一层全连接层进行测试

 

 这个对比就很明显了，拟合相对于之前的3层快了许多

2. 激活函数
self.sigmiod = nn.Sigmoid()

下面是网上找的

激活函数是神经网络中的一个重要组成部分，它的作用是将神经元的输入（加权和加偏置）转换为输出，从而引入非线性的变换。激活函数可以增强神经网络的表达能力和学习能力，使其能够拟合复杂的函数和数据分布。不同的激活函数有不同的特点和适用场景，一般来说，需要考虑以下几个方面：

• 激活函数的输出范围是否有限。有限的输出范围可以避免梯度爆炸或者消失的问题，也可以提高数值稳定性。比如Sigmoid函数的输出范围是(0,1)，而ReLU函数的输出范围是[0, +∞)。
• 激活函数是否是单调的。单调的激活函数可以保证误差函数是凸函数，从而避免局部最优解。比如Sigmoid函数和ReLU函数都是单调的，而双曲正切函数(tanh)则不是。
• 激活函数是否是可导的。可导的激活函数可以利用反向传播算法来更新权重和偏置，从而提高训练效率。比如Sigmoid函数和tanh函数都是可导的，而阶跃函数(step)则不是。
• 激活函数是否具有稀疏性。稀疏性指的是激活函数的输出大部分是零或者接近零，这样可以减少计算量和存储空间，也可以增强模型的泛化能力。比如ReLU函数和最大值整流线性单元(maxout)都具有稀疏性，而Sigmoid函数和tanh函数则不具有。

而在本例题中（八个特征点的糖尿病模型）：

进行ReLU 的尝试

代码如下：

import torch.nn as nn
import numpy as np
import torch

import matplotlib.pyplot as plt



xy = np.loadtxt('diabetes.csv', delimiter=',', dtype=np.float32, skiprows=1)
x_data = torch.from_numpy(xy[:, :-1])
y_data = torch.from_numpy(xy[:, [-1]])
epoch_list = []
loss_list = []
class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = nn.Linear(8, 6)
        self.linear2 = nn.Linear(6, 4)
        self.linear3 = nn.Linear(4, 2)
        self.linear4 = nn.Linear(2, 1)
        self.sigmiod = nn.Sigmoid()
        self.activate = nn.ReLU()
    def forward(self, x):
        x = self.activate(self.linear1(x))
        x = self.activate(self.linear2(x))
        x = self.activate(self.linear3(x))
        x = self.sigmiod(self.linear4(x))
        return x

model = Model()
criterion = nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(), lr=1.0)


for epoch in range(100):
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    loss_list.append(loss.item())
    epoch_list.append(epoch)
    print(epoch, loss.item())
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()



plt.plot(loss_list,epoch_list)

plt.show()

 问题： 最后一行使用sigmiod激活的目的

x = self.activate(self.linear1(x))
x = self.activate(self.linear2(x))
x = self.activate(self.linear3(x))
x = self.sigmiod(self.linear4(x))

最后一行使用Sigmoid激活的目的是将输出层的值映射到(0,1)之间，从而可以用于二分类问题或者作为概率输出。比如，如果输出层的值接近1，那么可以认为模型预测的类别是1，或者模型对类别1的置信度很高；如果输出层的值接近0，那么可以认为模型预测的类别是0，或者模型对类别0的置信度很高。

这是比较理论的原因， 另一个原因 是我觉得非常重要的：

ReLU函数的输出范围是[0, +∞)  在梯度运算的时候会出现负数 无法求log 值， 实践表示在跑模型的时候如果只是单纯的使用ReLU函数 有时候会报错 并且曲线 也经常不稳定， 然而使用Sigmoid激活 作为最后一层限制在（0 ，1）的范围 ，很大程度上解决了问题

具体情况建议可以亲自尝试看看

3.数据集的获取

这个例子使用的数据集是   Pima Indians Diabetes Database，直接打开链接下载即可

Pima Indians Diabetes Database | KagglePima Indians Diabetes Database | KagglePima Indians Diabetes Database | Kaggle