pytorch-softmax解决分类问题，用fashion-mnist为例子，再走一遍数据获取到模型预测的流程。深度了解分类指标的递进关系

• softmax回归

  • 线性回归模型适用于输出为连续值的情景。在另一类情景中，模型输出可以是一个像图像类别这样的离散值。对于这样的离散值预测问题，我们可以使用诸如softmax回归在内的分类模型。和线性回归不同，softmax回归的输出单元从一个变成了多个，且引入了softmax运算使输出更适合离散值的预测和训练。本节以softmax回归模型为例，介绍神经网络中的分类模型。

• 分类问题

  • 一个简单的图像分类问题，其输入图像的高和宽均为2像素，且色彩为灰度。这样每个像素值都可以用一个标量表示。我们将图像中的4像素分别记为$x_1,x_2,x_3,x_4$。假设训练数据集中图像的真实标签为狗、猫或鸡（假设可以用4像素表示出这3种动物），这些标签分别对应离散值$y_1,y_2,y_3$。

  • 通常使用离散的数值来表示类别，例如$y_1=1,y_2=2,y_3=3$。如此，一张图像的标签为1、2和3这3个数值中的一个。虽然仍然可以使用回归模型来进行建模，并将预测值就近定点化到1、2和3这3个离散值之一，但这种连续值到离散值的转化通常会影响到分类质量。因此一般使用更加适合离散值输出的模型来解决分类问题。

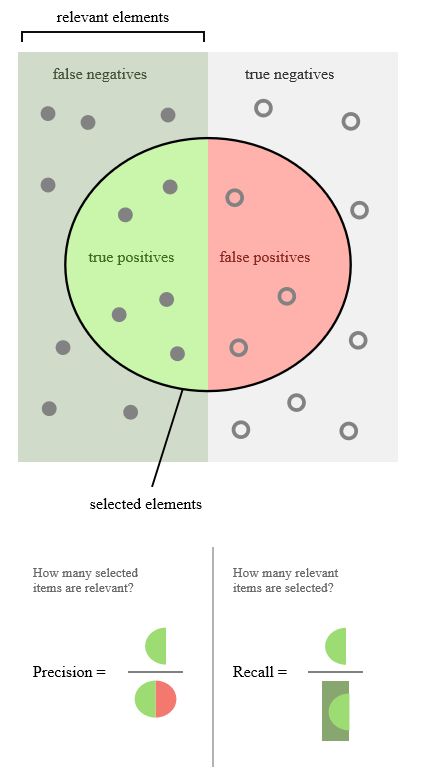
  • 机器学习分类任务的常用评价指标：准确率（Accuracy）、精确率（Precision）、召回率（Recall）、P-R曲线（Precision-Recall Curve）、F1 Score、混淆矩阵（Confuse Matrix）、ROC、AUC。

  • 准确率是分类问题中最为原始的评价指标，准确率的定义是预测正确的结果占总样本的百分比，其公式如下：

    • $$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$$
    • • 真正例(True Positive, TP)：被模型预测为正的正样本；
      • 假正例(False Positive, FP)：被模型预测为正的负样本；
      • 假负例(False Negative, FN)：被模型预测为负的正样本；
      • 真负例(True Negative, TN)：被模型预测为负的负样本；
    • 但是，准确率评价算法有一个明显的弊端问题，就是在数据的类别不均衡，特别是有极偏的数据存在的情况下，准确率这个评价指标是不能客观评价算法的优劣的。例如下面这个例子：
      • 在测试集里，有100个sample，99个反例，只有1个正例。如果我的模型不分青红皂白对任意一个sample都预测是反例，那么我的模型的准确率就为0.99，从数值上看是非常不错的，但事实上，这样的算法没有任何的预测能力，于是我们就应该考虑是不是评价指标出了问题，这时就需要使用其他的评价指标综合评判了。

  • 精准率（Precision）又叫查准率，它是针对预测结果而言的，它的含义是在所有被预测为正的样本中实际为正的样本的概率，意思就是在预测为正样本的结果中，我们有多少把握可以预测正确，其公式如下：

    • $$Precision=\frac{TP}{TP+FP}$$

  • 召回率（Recall）又叫查全率，它是针对原样本而言的，它的含义是在实际为正的样本中被预测为正样本的概率，其公式如下：

    • $$Recall=\frac{TP}{TP+FN}$$

    • 

    • 在不同的应用场景下，关注点不同，例如，在预测股票的时候，更关心精准率，即我们预测升的那些股票里，真的升了有多少，因为那些我们预测升的股票都是我们投钱的。而在预测病患的场景下，更关注召回率，即真的患病的那些人里我们预测错了情况应该越少越好。

    • 精确率和召回率是一对此消彼长的度量。例如在推荐系统中，我们想让推送的内容尽可能用户全都感兴趣，那只能推送我们把握高的内容，这样就漏掉了一些用户感兴趣的内容，召回率就低了；如果想让用户感兴趣的内容都被推送，那只有将所有内容都推送上，宁可错杀一千，不可放过一个，这样准确率就很低了。

  • P-R曲线

    • P-R曲线（Precision Recall Curve）正是描述精确率/召回率变化的曲线，P-R曲线定义如下：根据学习器的预测结果（一般为一个实值或概率）对测试样本进行排序，将最可能是“正例”的样本排在前面，最不可能是“正例”的排在后面，按此顺序逐个把样本作为“正例”进行预测，每次计算出当前的P值和R值，如下图所示：

    • 

    • P-R曲线如何评估呢？若一个学习器A的P-R曲线被另一个学习器B的P-R曲线完全包住，则称：B的性能优于A。若A和B的曲线发生了交叉，则谁的曲线下的面积大，谁的性能更优。但一般来说，曲线下的面积是很难进行估算的，所以衍生出了“平衡点”（Break-Event Point，简称BEP），即当P=R时的取值，平衡点的取值越高，性能更优。

  • F1-Score

    • Precision和Recall指标有时是此消彼长的，即精准率高了，召回率就下降，在一些场景下要兼顾精准率和召回率，最常见的方法就是F-Measure，又称F-Score。F-Measure是P和R的加权调和平均，即：
    • $$\frac{1}{F_{\beta }}=\frac{1}{1+{\beta }^2}\cdot (\frac{1}{P}+\frac{{\beta }^2}{R})$$
    • 特别地，当β=1时，也就是常见的F1-Score，是P和R的调和平均，当F1较高时，模型的性能越好。
    • $$F_1=\frac{2\ast P\ast R}{P+R}$$

  • ROC曲线

    • ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类别不平衡（Class Imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化，ROC以及AUC可以很好的消除样本类别不平衡对指标结果产生的影响。
    • 另一个原因是，ROC和上面做提到的P-R曲线一样，是一种不依赖于阈值（Threshold）的评价指标，在输出为概率分布的分类模型中，如果仅使用准确率、精确率、召回率作为评价指标进行模型对比时，都必须时基于某一个给定阈值的，对于不同的阈值，各模型的Metrics结果也会有所不同，这样就很难得出一个很置信的结果。
    • 还要再介绍两个指标，这两个指标的选择使得ROC可以无视样本的不平衡。这两个指标分别是：灵敏度（sensitivity）和特异度（specificity），也叫做真正率（TPR）和假正率（FPR），具体公式如下。
      • 灵敏度和召回率是一模一样的，只是名字换了而已。真正率(True Positive Rate , TPR)，又称灵敏度：
      • $$TPR=\frac{TP}{TP+FN}=\frac{正样本预测正确数}{正样本数}$$
      • 假负率(False Negative Rate , FNR) ：
      • $$FNR=\frac{FN}{TP+FN}=\frac{正样本预测错误数}{正样本数}$$
      • 假正率(False Positive Rate , FPR) ：
      • $$FPR=\frac{FP}{TN+FP}=\frac{负样本预测错误数}{负样本数}$$
      • 真负率(True Negative Rate , TNR)，又称特异度：
      • $$TNR=\frac{TN}{TN+FP}=\frac{负样本预测正确数}{负样本数}$$
    • 灵敏度（真正率）TPR是正样本的召回率，特异度（真负率）TNR是负样本的召回率，而假负率$FNR=1-TPR$、假正率$FPR=1-TNR$，上述四个量都是针对单一类别的预测结果而言的，所以对整体样本是否均衡并不敏感。
      • 举个例子：假设总样本中，90%是正样本，10%是负样本。在这种情况下我们如果使用准确率进行评价是不科学的，但是用TPR和TNR却是可以的，因为TPR只关注90%正样本中有多少是被预测正确的，而与那10%负样本毫无关系，同理，FPR只关注10%负样本中有多少是被预测错误的，也与那90%正样本毫无关系。这样就避免了样本不平衡的问题。
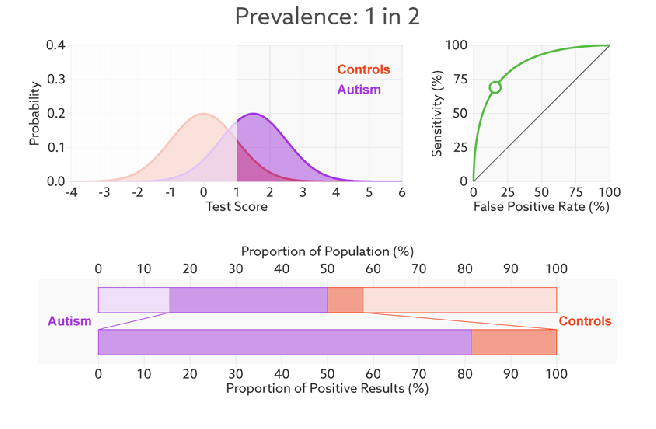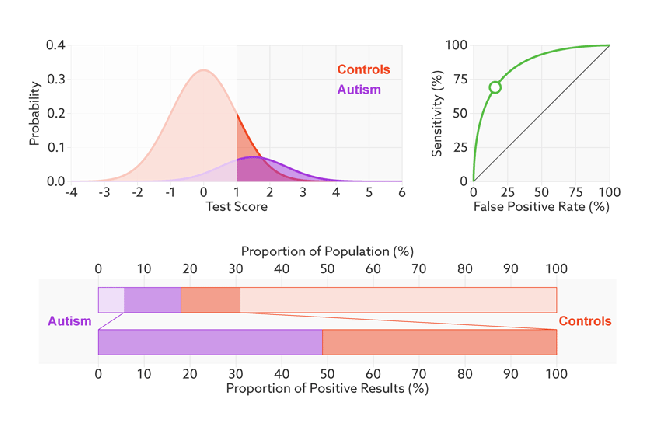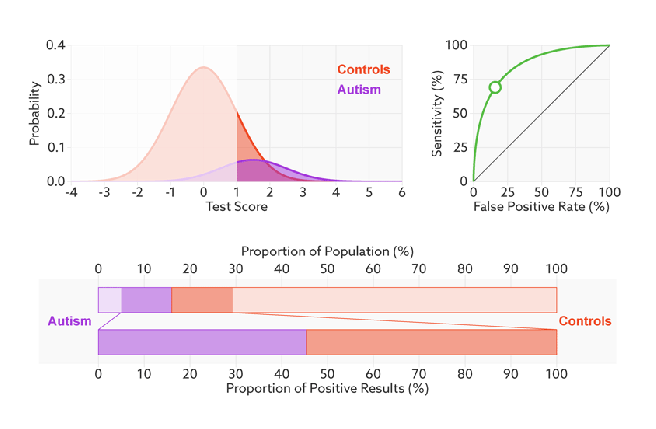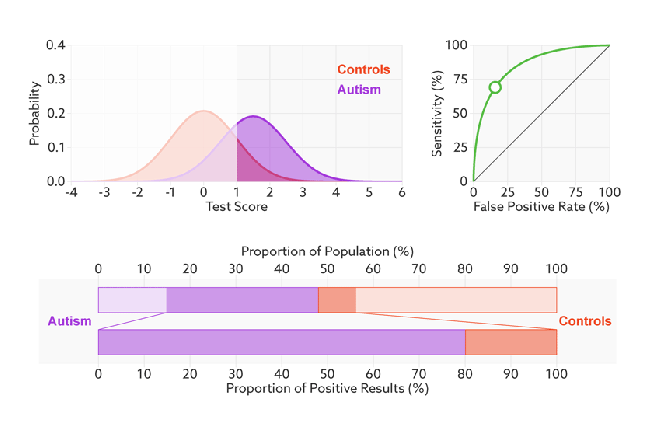
    • ROC（Receiver Operating Characteristic）曲线，又称接受者操作特征曲线。该曲线最早应用于雷达信号检测领域，用于区分信号与噪声。后来人们将其用于评价模型的预测能力。ROC曲线中的主要两个指标就是真正率TPR和假正率FPR，上面已经解释了这么选择的好处所在。其中横坐标为假正率（FPR），纵坐标为真正率（TPR），下面就是一个标准的ROC曲线图。

      • 

      • 阈值问题

        • 与前面的P-R曲线类似，ROC曲线也是通过遍历所有阈值来绘制整条曲线的。如果我们不断的遍历所有阈值，预测的正样本和负样本是在不断变化的，相应的在ROC曲线图中也会沿着曲线滑动。改变阈值只是不断地改变预测的正负样本数，即TPR和FPR，但是曲线本身并没有改变。这是有道理的，阈值并不会改变模型的性能。
        • 

      • 判断模型性能

        • 如何判断一个模型的ROC曲线是好的呢？这个还是要回归到我们的目的：FPR表示模型对于负样本误判的程度，而TPR表示模型对正样本召回的程度。我们所希望的当然是：负样本误判的越少越好，正样本召回的越多越好。所以总结一下就是**TPR越高，同时FPR越低（即ROC曲线越陡），那么模型的性能就越好。**参考如下动态图进行理解。即：进行模型的性能比较时，与PR曲线类似，若一个模型A的ROC曲线被另一个模型B的ROC曲线完全包住，则称B的性能优于A。若A和B的曲线发生了交叉，则谁的曲线下的面积大，谁的性能更优。
        • 

      • 无视样本不平衡

        • 对ROC曲线为什么可以无视样本不平衡做了解释，下面我们用动态图的形式再次展示一下它是如何工作的。我们发现：无论红蓝色样本比例如何改变，ROC曲线都没有影响。
        • 

  • AUC

    • AUC(Area Under Curve)又称为曲线下面积，是处于ROC Curve下方的那部分面积的大小。上文中已经提到，对于ROC曲线下方面积越大表明模型性能越好，于是AUC就是由此产生的评价指标。通常，AUC的值介于0.5到1.0之间，较大的AUC代表了较好的Performance。如果模型是完美的，那么它的AUC = 1，证明所有正例排在了负例的前面，如果模型是个简单的二类随机猜测模型，那么它的AUC = 0.5，如果一个模型好于另一个，则它的曲线下方面积相对较大，对应的AUC值也会较大。
    • AUC对所有可能的分类阈值的效果进行综合衡量。首先AUC值是一个概率值，可以理解为随机挑选一个正样本以及一个负样本，分类器判定正样本分值高于负样本分值的概率就是AUC值。简言之，AUC值越大，当前的分类算法越有可能将正样本分值高于负样本分值，即能够更好的分类。
    • 对于多分类问题，或者在二分类问题中，我们有时候会有多组混淆矩阵，例如：多次训练或者在多个数据集上训练的结果，那么估算全局性能的方法有两种，分为宏平均（macro-average）和微平均（micro-average）。简单理解，宏平均就是先算出每个混淆矩阵的P值和R值，然后取得平均P值macro-P和平均R值macro-R，再算出$F_{\beta }$或$F_1$，而微平均则是计算出混淆矩阵的平均TP、FP、TN、FN，接着进行计算P、R，进而求出$F_{\beta }$或F1。其它分类指标同理，均可以通过宏平均/微平均计算得出。
    • 在多分类任务场景中，如果非要用一个综合考量的metric的话，宏平均会比微平均更好一些，因为宏平均受稀有类别影响更大。宏平均平等对待每一个类别，所以它的值主要受到稀有类别的影响，而微平均平等考虑数据集中的每一个样本，所以它的值受到常见类别的影响比较大。
      • $$\begin{gathered} macroP=\frac{1}{n}\sum _{i=1}^n{P}_i,macroR=\frac{1}{n}\sum _{i=1}^n{R}_i \\ macro{F}_1=\frac{2\ast macroP\ast macroR}{macroP+macroR} \\ microP=\frac{\overline{TP}}{\overline{TP}+\overline{FP}},microR=\frac{\overline{TP}}{\overline{TP}+\overline{FN}} \\ micro{F}_1=\frac{2\ast microP\ast microR}{microP+microR} \end{gathered}$$

  • https://www.guoyaohua.com/classification-metrics.html
    

• softmax回归模型

  • softmax回归跟线性回归一样将输入特征与权重做线性叠加。与线性回归的一个主要不同在于，softmax回归的输出值个数等于标签里的类别数。因为一共有4种特征和3种输出动物类别，所以权重包含12个标量（带下标的w）、偏差包含3个标量（带下标的b），且对每个输入计算$o_1,o_2,o_3$这3个输出：
  • $$\begin{array}{rl}{o}_1& =x_1{w}_{11}+x_2{w}_{21}+x_3{w}_{31}+x_4{w}_{41}+b_1,\\ o_2& =x_1{w}_{12}+x_2{w}_{22}+x_3{w}_{32}+x_4{w}_{42}+b_2,\\ o_3& =x_1{w}_{13}+x_2{w}_{23}+x_3{w}_{33}+x_4{w}_{43}+b_3.\end{array}$$
  • 既然分类问题需要得到离散的预测输出，一个简单的办法是将输出值$o_i$当作预测类别是i的置信度，并将值最大的输出所对应的类作为预测输出，即输出 $\underset{i}{\mathrm{argmax}}{o}_i$。例如，如果$o_1,o_2,o_3$分别为0.1,10,0.1，由于$o_2$最大，那么预测类别为2，其代表猫。
  • 然而，直接使用输出层的输出有两个问题。一方面，由于输出层的输出值的范围不确定，我们难以直观上判断这些值的意义。例如，刚才举的例子中的输出值10表示“很置信”图像类别为猫，因为该输出值是其他两类的输出值的100倍。但如果$o_1=o_3=10^3$，那么输出值10却又表示图像类别为猫的概率很低。另一方面，由于真实标签是离散值，这些离散值与不确定范围的输出值之间的误差难以衡量。softmax运算符（softmax operator）解决了以上两个问题。它通过下式将输出值变换成值为正且和为1的概率分布：
  • $$\begin{gathered} {\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3=\text{softmax}(o_1,o_2,o_3) \\ {\hat{y}}_1=\frac{\exp (o_1)}{{\sum }_{i=1}^3\exp (o_i)},{\hat{y}}_2=\frac{\exp (o_2)}{{\sum }_{i=1}^3\exp (o_i)},{\hat{y}}_3=\frac{\exp (o_3)}{{\sum }_{i=1}^3\exp (o_i)}. \end{gathered}$$
  • 容易看出${\hat{y}}_1+{\hat{y}}_2+{\hat{y}}_3=1$且$0\le {\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3\le 1$，因此${\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3$是一个合法的概率分布。这时候，如果${\hat{y}}_2=0.8$，不管${\hat{y}}_1$和${\hat{y}}_3$的值是多少，都知道图像类别为猫的概率是80%。此外
  • $$\underset{i}{\mathrm{argmax}}{o}_i=\underset{i}{\mathrm{argmax}}{\hat{y}}_i$$
  • 因此softmax运算不改变预测类别输出。

• 交叉熵损失函数

  • 使用softmax运算后可以更方便地与离散标签计算误差。已经知道，softmax运算将输出变换成一个合法的类别预测分布。实际上，真实标签也可以用类别分布表达：对于样本i，构造向量${\mathbf{y}}^{(i)}\in {\mathbb{R}}^q$ ，使其第$y^{(i)}$（样本i类别的离散数值）个元素为1，其余为0。这样训练目标可以设为使预测概率分布${\hat{\mathbf{y}}}^{(i)}$尽可能接近真实的标签概率分布${\mathbf{y}}^{(i)}$。
  • 可以像线性回归那样使用平方损失函数$|{\hat{\mathbf{y}}}^{(i)}-{\mathbf{y}}^{(i)}{|}^2/2$。然而，想要预测分类结果正确，其实并不需要预测概率完全等于标签概率。例如，在图像分类的例子里，如果$y^{(i)}=3$，那么只需要${\hat{y}}_3^{(i)}$比其他两个预测值${\hat{y}}_1^{(i)}$和${\hat{y}}_2^{(i)}$大就行了。即使${\hat{y}}_3^{(i)}$值为0.6，不管其他两个预测值为多少，类别预测均正确。而平方损失则过于严格，例如${\hat{y}}_1^{(i)}={\hat{y}}_2^{(i)}=0.2$比${\hat{y}}_1^{(i)}=0,{\hat{y}}_2^{(i)}=0.4$的损失要小很多，虽然两者都有同样正确的分类预测结果。
  • 改善上述问题的一个方法是使用更适合衡量两个概率分布差异的测量函数。其中，交叉熵（cross entropy）是一个常用的衡量方法：
    • $$H\left({\mathbf{y}}^{(i)},{\hat{\mathbf{y}}}^{(i)}\right)=-\sum _{j=1}^q{y}_j^{(i)}\log {\hat{y}}_j^{(i)}$$
  • 其中带下标的$y_j^{(i)}$是向量${\mathbf{y}}^{(i)}$中非0即1的元素，需要注意将它与样本i类别的离散数值，即不带下标的$y^{(i)}$区分。在上式中，向量${\mathbf{y}}^{(i)}$中只有第$y^{(i)}$个元素$y^{(i)}\ast y^{(i)}$为1，其余全为0，于是$H({\mathbf{y}}^{(i)},{\hat{\mathbf{y}}}^{(i)})=-\log \hat{y}\ast {y^{(i)}}^{(i)}$。也就是说，交叉熵只关心对正确类别的预测概率，因为只要其值足够大，就可以确保分类结果正确。当然，遇到一个样本有多个标签时，例如图像里含有不止一个物体时，并不能做这一步简化。但即便对于这种情况，交叉熵同样只关心对图像中出现的物体类别的预测概率。
  • 假设训练数据集的样本数为n，交叉熵损失函数定义为$\ell (\mathbf{\Theta })=\frac{1}{n}{\sum }_{i=1}^{n}H\left({\mathbf{y}}^{(i)},{\hat{\mathbf{y}}}^{(i)}\right)$,其中$\mathbf{\Theta }$代表模型参数。同样地，如果每个样本只有一个标签，那么交叉熵损失可以简写成$\ell (\mathbf{\Theta })=-(1/n){\sum }_{i=1}^n\log {\hat{y}}_{y^{(i)}}^{(i)}$。从另一个角度来看，最小化$\ell (\mathbf{\Theta })$等价于最大化$\exp (-n\ell (\mathbf{\Theta }))={\prod }_{i=1}^n{\hat{y}}_{y^{(i)}}^{(i)}$，即最小化交叉熵损失函数等价于最大化训练数据集所有标签类别的联合预测概率。
  • softmax回归适用于分类问题。它使用softmax运算输出类别的概率分布。softmax回归是一个单层神经网络，输出个数等于分类问题中的类别个数。交叉熵适合衡量两个概率分布的差异。

• 模型预测及评价

  • 在训练好softmax回归模型后，给定任一样本特征，就可以预测每个输出类别的概率。通常，把预测概率最大的类别作为输出类别。如果它与真实类别（标签）一致，说明这次预测是正确的。后文将使用准确率（accuracy）来评价模型的表现。它等于正确预测数量与总预测数量之比。

• 图像分类实践

  • 多类图像分类数据集。它将在后面的章节中被多次使用，以方便观察比较算法之间在模型精度和计算效率上的区别。图像分类数据集中最常用的是手写数字识别数据集MNIST。但大部分模型在MNIST上的分类精度都超过了95%。为了更直观地观察算法之间的差异，将使用一个图像内容更加复杂的数据集Fashion-MNIST（这个数据集也比较小，只有几十M，没有GPU的电脑也能吃得消）。
  • 本节将使用torchvision包，它是服务于PyTorch深度学习框架的，主要用来构建计算机视觉模型。torchvision主要由以下几部分构成：
    • torchvision.datasets: 一些加载数据的函数及常用的数据集接口；
  • torchvision.models: 包含常用的模型结构（含预训练模型），例如AlexNet、VGG、ResNet等；
  • torchvision.transforms: 常用的图片变换，例如裁剪、旋转等；
  • torchvision.utils: 其他的一些有用的方法。

• 获取数据集

  • 检测自己当前的环境

  • import torch
    print(torch.__version__)
    print(torch.cuda.is_available())
    print(torch.backends.cudnn.enabled)
    print(torch.backends.cudnn.enabled)
    print(torch.backends.cudnn.deterministic)
    

  • 1.13.1
    False
    True
    True
    False
    

• 设置 torch.backends.cudnn.benchmark=True 将会让程序在开始时花费一点额外时间，为整个网络的每个卷积层搜索最适合它的卷积实现算法，进而实现网络的加速。可以让内置的 cuDNN 的 auto-tuner 自动寻找最适合当前配置的高效算法，来达到优化运行效率的问题。适用场景是网络结构固定（不是动态变化的），网络的输入形状（包括 batch size，图片大小，输入的通道）是不变的，其实也就是一般情况下都比较适用。反之，如果卷积层的设置一直变化，网络的输入数据在每次 iteration 都变化的话，会导致 cnDNN 每次都会去寻找一遍最优配置，这样反而会降低运行效率。

• Benchmark模式会提升计算速度，但是由于计算中有随机性，每次网络前馈结果略有差异。如果想要避免这种结果波动，设置：

  • import torch.backends.cudnn as cudnn
    cudnn.deterministic = True
    cudnn.benchmark = True
    torch.backends.cudnn.enabled = True
    print(torch.backends.cudnn.enabled)
    print(torch.backends.cudnn.enabled)
    print(torch.backends.cudnn.deterministic)
    

  • True
    True
    True
    

• 导入所需模块

  • import torch
    import torchvision
    import torchvision.transforms as transforms
    import matplotlib.pyplot as plt
    import time
    import sys
    

• 通过torchvision的torchvision.datasets来下载这个数据集。第一次调用时会自动从网上获取数据，后面没有删除的话就不用再下载了。我们通过参数train来指定获取训练数据集或测试数据集（testing data set）。测试数据集也叫测试集（testing set），只用来评价模型的表现，并不用来训练模型。

• 另外还指定了参数transform = transforms.ToTensor()使所有数据转换为Tensor，如果不进行转换则返回的是PIL图片。transforms.ToTensor()将尺寸为 (H x W x C) 且数据位于[0, 255]的PIL图片或者数据类型为np.uint8的NumPy数组转换为尺寸为(C x H x W)且数据类型为torch.float32且位于[0.0, 1.0]的Tensor。

  • 注意： 由于像素值为0到255的整数，所以刚好是uint8所能表示的范围，包括transforms.ToTensor()在内的一些关于图片的函数就默认输入的是uint8型，若不是，可能不会报错但可能得不到想要的结果。所以，如果用像素值(0-255整数)表示图片数据，那么一律将其类型设置成uint8，避免不必要的bug。

• mnist_train = torchvision.datasets.FashionMNIS(root='~/Datasets/FashionMNIST', train=True, download=True, transform=transforms.ToTensor())
  mnist_test = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=False, download=True, transform=transforms.ToTensor())
  

  • Downloading http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/train-images-idx3-ubyte.gz
    Downloading http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/train-images-idx3-ubyte.gz to C:\Users\23105/Datasets/FashionMNIST\FashionMNIST\raw\train-images-idx3-ubyte.gz
    100.0%
    Extracting C:\Users\23105/Datasets/FashionMNIST\FashionMNIST\raw\train-images-idx3-ubyte.gz to C:\Users\23105/Datasets/FashionMNIST\FashionMNIST\raw
    Downloading http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/train-labels-idx1-ubyte.gz
    Downloading http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/train-labels-idx1-ubyte.gz to C:\Users\23105/Datasets/FashionMNIST\FashionMNIST\raw\train-labels-idx1-ubyte.gz
    100.0%
    Extracting C:\Users\23105/Datasets/FashionMNIST\FashionMNIST\raw\train-labels-idx1-ubyte.gz to C:\Users\23105/Datasets/FashionMNIST\FashionMNIST\raw
    Downloading http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/t10k-images-idx3-ubyte.gz
    Downloading http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/t10k-images-idx3-ubyte.gz to C:\Users\23105/Datasets/FashionMNIST\FashionMNIST\raw\t10k-images-idx3-ubyte.gz
    100.0%
    Extracting C:\Users\23105/Datasets/FashionMNIST\FashionMNIST\raw\t10k-images-idx3-ubyte.gz to C:\Users\23105/Datasets/FashionMNIST\FashionMNIST\raw
    Downloading http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/t10k-labels-idx1-ubyte.gz
    Downloading http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/t10k-labels-idx1-ubyte.gz to C:\Users\23105/Datasets/FashionMNIST\FashionMNIST\raw\t10k-labels-idx1-ubyte.gz
    100.0%
    Extracting C:\Users\23105/Datasets/FashionMNIST\FashionMNIST\raw\t10k-labels-idx1-ubyte.gz to C:\Users\23105/Datasets/FashionMNIST\FashionMNIST\raw
    ag-0-1gqbvl5ecag-1-1gqbvl5ec
    

• 上面的mnist_train和mnist_test都是torch.utils.data.Dataset的子类，所以我们可以用len()来获取该数据集的大小，还可以用下标来获取具体的一个样本。训练集中和测试集中的每个类别的图像数分别为6,000和1,000。因为有10个类别，所以训练集和测试集的样本数分别为60,000和10,000。

• print(type(mnist_train))
  print(len(mnist_train), len(mnist_test))
  feature, label = mnist_train[100]
  print(feature.shape, label)  # Channel x Height x Width
  

  • <class 'torchvision.datasets.mnist.FashionMNIST'>
    60000 10000
    torch.Size([1, 28, 28]) 8
    

• 变量feature对应高和宽均为28像素的图像。由于使用了transforms.ToTensor()，所以每个像素的数值为[0.0, 1.0]的32位浮点数。需要注意的是，feature的尺寸是 (C x H x W) 的，而不是 (H x W x C)。第一维是通道数，因为数据集中是灰度图像，所以通道数为1。后面两维分别是图像的高和宽。

• Fashion-MNIST中一共包括了10个类别，分别为t-shirt（T恤）、trouser（裤子）、pullover（套衫）、dress（连衣裙）、coat（外套）、sandal（凉鞋）、shirt（衬衫）、sneaker（运动鞋）、bag（包）和ankle boot（短靴）。以下函数可以将数值标签转成相应的文本标签。

• from IPython import display
  def get_fashion_mnist_labels(labels):
      text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                     'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
      return [text_labels[int(i)] for i in labels]
  def use_svg_display():
      # 用矢量图显示
      display.display_svg()
  def show_fashion_mnist(images, labels):
      use_svg_display()
      # 这里的_表示我们忽略（不使用）的变量
      _, figs = plt.subplots(1, len(images), figsize=(12, 12))
      for f, img, lbl in zip(figs, images, labels):
          f.imshow(img.view((28, 28)).numpy())
          f.set_title(lbl)
          f.axes.get_xaxis().set_visible(False)
          f.axes.get_yaxis().set_visible(False)
      plt.show()
  X, y = [], []
  for i in range(10):
      X.append(mnist_train[i][0])
      y.append(mnist_train[i][1])
  show_fashion_mnist(X, get_fashion_mnist_labels(y))
  

  • 

• 读取小批量

  • 将在训练数据集上训练模型，并将训练好的模型在测试数据集上评价模型的表现。前面说过，mnist_train是torch.utils.data.Dataset的子类，所以我们可以将其传入torch.utils.data.DataLoader来创建一个读取小批量数据样本的DataLoader实例。在实践中，数据读取经常是训练的性能瓶颈，特别当模型较简单或者计算硬件性能较高时。PyTorch的DataLoader中一个很方便的功能是允许使用多进程来加速数据读取。这里我们通过参数num_workers来设置4个进程(和CPU，内存条的性能有关)读取数据。

  • batch_size = 256
    if sys.platform.startswith('win'):
        num_workers = 0  # 0表示不用额外的进程来加速读取数据
        print("windows")
    else:
        num_workers = 4
    train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
    test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)
    start = time.time()
    for X, y in train_iter:
        continue
    print('%.2f sec' % (time.time() - start))
    

  • windows
    8.13 sec
    

  • 每次dataloader加载数据时：dataloader一次性创建num_worker个worker，（也可以说dataloader一次性创建num_worker个工作进程，worker也是普通的工作进程），并用batch_sampler将指定batch分配给指定worker，worker将它负责的batch加载进RAM。然后，dataloader从RAM中找本轮迭代要用的batch，如果找到了，就使用。如果没找到，就要num_worker个worker继续加载batch到内存，直到dataloader在RAM中找到目标batch。一般情况下都是能找到的，因为batch_sampler指定batch时当然优先指定本轮要用的batch。

  • num_worker设置得大，好处是寻batch速度快，因为下一轮迭代的batch很可能在上一轮/上上一轮…迭代时已经加载好了。坏处是内存开销大，也加重了CPU负担（worker加载数据到RAM的进程是CPU复制的嘛）。num_workers的经验设置值是自己电脑/服务器的CPU核心数，如果CPU很强、RAM也很充足，就可以设置得更大些。

  • 如果num_worker设为0，意味着每一轮迭代时，dataloader不再有自主加载数据到RAM这一步骤（因为没有worker了），而是在RAM中找batch，找不到时再加载相应的batch。缺点当然是速度更慢。

• softmax回归的从零开始实现

  • 导包，加载数据

  • import torch
    import torchvision
    import numpy as np
    import sys  
    def load_data_fashion_mnist(batch_size, resize=None, root='~/Datasets/FashionMNIST'):
        """Download the fashion mnist dataset and then load into memory."""
        trans = []
        if resize:
            trans.append(torchvision.transforms.Resize(size=resize))
        trans.append(torchvision.transforms.ToTensor())
    
        transform = torchvision.transforms.Compose(trans)
        mnist_train = torchvision.datasets.FashionMNIST(root=root, train=True, download=True, transform=transform)
        mnist_test = torchvision.datasets.FashionMNIST(root=root, train=False, download=True, transform=transform)
        if sys.platform.startswith('win'):
            num_workers = 0  # 0表示不用额外的进程来加速读取数据
        else:
            num_workers = 4
        train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
        test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)
        return train_iter, test_iter
    batch_size = 256
    train_iter, test_iter = load_data_fashion_mnist(batch_size)
    print(train_iter, test_iter)
    

  • <torch.utils.data.dataloader.DataLoader object at 0x000001FE0A84DA60> <torch.utils.data.dataloader.DataLoader object at 0x000001FE0A8C3340>
    

  • 初始化模型参数：跟线性回归中的例子一样，我们将使用向量表示每个样本。已知每个样本输入是高和宽均为28像素的图像。模型的输入向量的长度是 $28\times 28=784$：该向量的每个元素对应图像中每个像素。由于图像有10个类别，单层神经网络输出层的输出个数为10，因此softmax回归的权重和偏差参数分别为$784\times 10$和$1\times 10$的矩阵。

  • num_inputs = 784
    num_outputs = 10
    W = torch.tensor(np.random.normal(0, 0.01, (num_inputs, num_outputs)), dtype=torch.float)
    b = torch.zeros(num_outputs, dtype=torch.float)
    W.requires_grad_(requires_grad=True)
    b.requires_grad_(requires_grad=True) 
    

  • 在下面的函数中，矩阵X的行数是样本数，列数是输出个数。为了表达样本预测各个输出的概率，softmax运算会先通过exp函数对每个元素做指数运算，再对exp矩阵同行元素求和，最后令矩阵每行各元素与该行元素之和相除。这样一来，最终得到的矩阵每行元素和为1且非负。因此，该矩阵每行都是合法的概率分布。softmax运算的输出矩阵中的任意一行元素代表了一个样本在各个输出类别上的预测概率。

  • def softmax(X):
        X_exp = X.exp()
        partition = X_exp.sum(dim=1, keepdim=True)
        return X_exp / partition  # 这里应用了广播机制
    X = torch.rand((2, 5))
    X_prob = softmax(X)
    print(X_prob, X_prob.sum(dim=1))
    

  • tensor([[0.2863, 0.1637, 0.2700, 0.1196, 0.1604],
            [0.1317, 0.2498, 0.2233, 0.2249, 0.1703]]) tensor([1.0000, 1.0000])
    

  • 可以看到，对于随机输入，我们将每个元素变成了非负数，且每一行和为1

  • 定义模型

    • 有了softmax运算，可以定义上节描述的softmax回归模型了。这里通过view函数将每张原始图像改成长度为num_inputs的向量。

    • softmax回归使用的交叉熵损失函数。为了得到标签的预测概率，可以使用gather函数。在下面的例子中，变量y_hat是2个样本在3个类别的预测概率，变量y是这2个样本的标签类别。通过使用gather函数，得到了2个样本的标签的预测概率。前文（softmax回归）数学表述中标签类别离散值从1开始逐一递增不同，在代码中，标签类别的离散值是从0开始逐一递增的。

    • def net(X):
          return softmax(torch.mm(X.view((-1, num_inputs)), W) + b)
      y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
      y = torch.LongTensor([0, 2])
      y_hat.gather(1, y.view(-1, 1))
      print(y_hat)
      print(y_hat.gather(1, y.view(-1, 1)))
      

    • tensor([[0.1000, 0.3000, 0.6000],
              [0.3000, 0.2000, 0.5000]])
      tensor([[0.1000ag-0-1gqdfqcemag-1-1gqdfqcemag-0-1gqdfqcemag-1-1gqdfqcem],
              [0.5000]])
      

  • 交叉熵损失函数。可以评价模型net在数据集data_iter上的准确率。随机初始化了模型net，所以这个随机模型的准确率应该接近于类别个数10的倒数即0.1。

    • def net(X):
          return softmax(torch.mm(X.view((-1, num_inputs)), W) + b)
      def cross_entropy(y_hat, y):
          return - torch.log(y_hat.gather(1, y.view(-1, 1)))
      def accuracy(y_hat, y):
          return (y_hat.argmax(dim=1) == y).float().mean().item()
      def evaluate_accuracy(data_iter, net):
          acc_sum, n = 0.0, 0
          for X, y in data_iter:
              acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
              n += y.shape[0]
          return acc_sum / n
      print(evaluate_accuracy(test_iter, net))
      

    • 0.132
      

    • 给定一个类别的预测概率分布y_hat，我们把预测概率最大的类别作为输出类别。如果它与真实类别y一致，说明这次预测是正确的。分类准确率即正确预测数量与总预测数量之比。

  • 训练模型

    • 训练softmax回归的实现线性回归的实现介绍的线性回归中的实现非常相似。同样使用小批量随机梯度下降来优化模型的损失函数。在训练模型时，迭代周期数num_epochs和学习率lr都是可以调的超参数。改变它们的值可能会得到分类更准确的模型。

    • num_epochs, lr = 5, 0.1
      def sgd(params, lr, batch_size): 
          for param in params:
              param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data
      def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
                    params=None, lr=None, optimizer=None):
          for epoch in range(num_epochs):
              train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
              for X, y in train_iter:
                  y_hat = net(X)
                  l = loss(y_hat, y).sum()
                  # 梯度清零
                  if optimizer is not None:
                      optimizer.zero_grad()
                  elif params is not None and params[0].grad is not None:
                      for param in params:
                          param.grad.data.zero_()
                  l.backward()
                  if optimizer is None:
                      sgd(params, lr, batch_size)
                  else:
                      optimizer.step()  # “softmax回归的简洁实现”一节将用到
                  train_l_sum += l.item()
                  train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
                  n += y.shape[0]
              test_acc = evaluate_accuracy(test_iter, net)
              print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
                    % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
      train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, batch_size, [W, b], lr)
      

    • epoch 1, loss 0.4740, train acc 0.840, test acc 0.824
      epoch 2, loss 0.4657, train acc 0.842, test acc 0.826
      epoch 3, loss 0.4577, train acc 0.844, test acc 0.833
      epoch 4, loss 0.4516, train acc 0.848, test acc 0.835
      epoch 5, loss 0.4474, train acc 0.849, test acc 0.832
      epoch 6, loss 0.4428, train acc 0.849, test acc 0.835
      epoch 7, loss 0.4391, train acc 0.851, test acc 0.836
      epoch 8, loss 0.4364, train acc 0.851, test acc 0.837
      epoch 9, loss 0.4335, train acc 0.852, test acc 0.835
      epoch 10, loss 0.4298, train acc 0.854, test acc 0.836
      

  • 预测

    • 训练完成后，现在就可以演示如何对图像进行分类了。给定一系列图像（第三行图像输出），我们比较一下它们的真实标签（第一行文本输出）和模型预测结果（第二行文本输出）。

    • from IPython import display
      from matplotlib import pyplot as plt
      def get_fashion_mnist_labels(labels):
          text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                         'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
          return [text_labels[int(i)] for i in labels]
      def use_svg_display():
          # 用矢量图显示
          display.display_svg()
      def show_fashion_mnist(images, labels):
          use_svg_display()
          # 这里的_表示我们忽略（不使用）的变量
          _, figs = plt.subplots(1, len(images), figsize=(12, 12))
          for f, img, lbl in zip(figs, images, labels):
              f.imshow(img.view((28, 28)).numpy())
              f.set_title(lbl)
              f.axes.get_xaxis().set_visible(False)
              f.axes.get_yaxis().set_visible(False)
          plt.show()
      Xag-0-1gqdfqcemag-1-1gqdfqcem, y = next(iter(test_iter))
      true_labels = get_fashion_mnist_labels(y.numpy())
      pred_labels = get_fashion_mnist_labels(net(X).argmax(dim=1).numpy())
      titles = [true + '\n' + pred for true, pred in zip(true_labels, pred_labels)]
      show_fashion_mnist(X[0:9], titles[0:9])
      

    • 

• 可以使用softmax回归做多类别分类。与训练线性回归相比，你会发现训练softmax回归的步骤和它非常相似：获取并读取数据、定义模型和损失函数并使用优化算法训练模型。事实上，绝大多数深度学习模型的训练都有着类似的步骤。

再次使用Pytorch来实现一个softmax回归模型。首先导入所需的包或模块。获取和读取数据.

• import torch
  from torch import nn
  from torch.nn import init
  import numpy as np
  import sys
  def load_data_fashion_mnist(batch_size, resize=None, root='~/Datasets/FashionMNIST'):
      """Download the fashion mnist dataset and then load into memory."""
      trans = []
      if resize:
          trans.append(torchvision.transforms.Resize(size=resize))
      trans.append(torchvision.transforms.ToTensor())
      transform = torchvision.transforms.Compose(trans)
      mnist_train = torchvision.datasets.FashionMNIST(root=root, train=True, download=True, transform=transform)
      mnist_test = torchvision.datasets.FashionMNIST(root=root, train=False, download=True, transform=transform)
      if sys.platform.startswith('win'):
          num_workers = 0  # 0表示不用额外的进程来加速读取数据
      else:
          num_workers = 4
      train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
      test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)
      return train_iter, test_iter
  batch_size = 256
  train_iter, test_iter = load_data_fashion_mnist(batch_size)
  print(train_iter, test_iter)
  

  • <torch.utils.data.dataloader.DataLoader object at 0x000001FE0DD008E0> <torch.utils.data.dataloader.DataLoader object at 0x000001FE0DD21340>
    

定义和初始化模型

• softmax回归的输出层是一个全连接层，所以我们用一个线性模块就可以了。因为前面我们数据返回的每个batch样本x的形状为(batch_size, 1, 28, 28), 所以我们要先用view()将x的形状转换成(batch_size, 784)才送入全连接层。

• num_inputs = 784
  num_outputs = 10
  class LinearNet(nn.Module):
      def __init__(self, num_inputs, num_outputs):
          super(LinearNet, self).__init__()
          self.linear = nn.Linear(num_inputs, num_outputs)
      def forward(self, x): # x shape: (batch, 1, 28, 28)
          y = self.linear(x.view(x.shape[0], -1))
          return y
  class FlattenLayer(nn.Module):
      def __init__(self):
          super(FlattenLayer, self).__init__()
      def forward(self, x): # x shape: (batch, *, *, ...)
          return x.view(x.shape[0], -1)
  net = LinearNet(num_inputs, num_outputs)
  print(net)
  from collections import OrderedDict
  net = nn.Sequential(
      # FlattenLayer(),
      # nn.Linear(num_inputs, num_outputs)
      OrderedDict([
          ('flatten', FlattenLayer()),
          ('linear', nn.Linear(num_inputs, num_outputs))
      ])
  )
  print(net)
  

• LinearNet(
    (linear): Linear(in_features=784, out_features=10, bias=True)
  )
  Sequential(
    (flatten): FlattenLayer()
    (linear): Linear(in_features=784, out_features=10, bias=True)
  )
  

• 将对x的形状转换的这个功能自定义一个`FlattenLayer。然后，使用均值为0、标准差为0.01的正态分布随机初始化模型的权重参数。

• init.normal_(net.linear.weight, mean=0, std=0.01)
  init.constant_(net.linear.bias, val=0) 
  

softmax和交叉熵损失函数

• 分开定义softmax运算和交叉熵损失函数可能会造成数值不稳定。因此，PyTorch提供了一个包括softmax运算和交叉熵损失计算的函数。它的数值稳定性更好。

• loss = nn.CrossEntropyLoss()
  

定义优化算法

• 使用学习率为0.1的小批量随机梯度下降作为优化算法。

• optimizer = torch.optim.SGD(net.parameters(), lr=0.1)
  

训练模型

• def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
                params=None, lr=None, optimizer=None):
      for epoch in range(num_epochs):
          train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
          for X, y in train_iter:
              y_hat = net(X)
              l = loss(y_hat, y).sum()
              # 梯度清零
              if optimizer is not None:
                  optimizer.zero_grad()
              elif params is not None and params[0].grad is not None:
                  for param in params:
                      param.grad.data.zero_()
              l.backward()
              if optimizer is None:
                  sgd(params, lr, batch_size)
              else:
                  optimizer.step()  # “softmax回归的简洁实现”一节将用到
              train_l_sum += l.item()
              train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
              n += y.shape[0]
          test_acc = evaluate_accuracy(test_iter, net)
          print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
                % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
  num_epochs = 10
  train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None, None, optimizer)
  

• epoch 1, loss 0.0031, train acc 0.749, test acc 0.796
  epoch 2, loss 0.0022, train acc 0.812, test acc 0.806
  epoch 3, loss 0.0021, train acc 0.826, test acc 0.809
  epoch 4, loss 0.0020, train acc 0.832, test acc 0.816
  epoch 5, loss 0.0019, train acc 0.837, test acc 0.824
  epoch 6, loss 0.0019, train acc 0.841, test acc 0.828
  epoch 7, loss 0.0018, train acc 0.843, test acc 0.830
  epoch 8, loss 0.0018, train acc 0.845, test acc 0.828
  epoch 9, loss 0.0018, train acc 0.846, test acc 0.829
  epoch 10, loss 0.0018, train acc 0.849, test acc 0.832
  

用pytorch构建的模型预测

• from IPython import display
  from matplotlib import pyplot as plt
  def get_fashion_mnist_labels(labels):
      text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                     'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
      return [text_labels[int(i)] for i in labels]
  def use_svg_display():
      # 用矢量图显示
      display.display_svg()
  def show_fashion_mnist(images, labels):
      use_svg_display()
      # 这里的_表示我们忽略（不使用）的变量
      _, figs = plt.subplots(1, len(images), figsize=(12, 12))
      for f, img, lbl in zip(figs, images, labels):
          f.imshow(img.view((28, 28)).numpy())
          f.set_title(lbl)
          f.axes.get_xaxis().set_visible(False)
          f.axes.get_yaxis().set_visible(False)
      plt.show()
  print(net)
  X, y = next(iter(test_iter))
  true_labels = get_fashion_mnist_labels(y.numpy())
  pred_labels = get_fashion_mnist_labels(net(X).argmax(dim=1).numpy())
  titles = [true + '\n' + pred for true, pred in zip(true_labels, pred_labels)]
  show_fashion_mnist(X[0:9], titles[0:9])
  

• 

• 如果没有进行模型训练，模型随机预测结果

•