leetcode刷题详解十四

39. 组合总和

vector> res;
vector temp;
vector> combinationSum(vector& candidates, int target) {
    back_tracing(candidates, 0, 0, target);
    return res;
}

void back_tracing(vector& candidates,int sum, int start, int target){
    if(sum == target){
        res.push_back(temp);
        return;
    }
    else if(sum > target ){
        return;
    }
    for(int i = start; i < candidates.size(); i++){
        temp.push_back(candidates[i]);
        sum += candidates[i];
        back_tracing(candidates, sum, i, target);
        sum -= candidates[i];
        temp.pop_back();
    }
}

• 重点总结

  这道题和77题组合问题的相同点和难点主要在于下面这几行代码：

  for(int i = start; i <= n; i++){
      //处理节点
      back_tracing(n, k, i+1);  
      /**或者**/   
      back_tracing(n, k, i)
  	//回溯
   }
  

  如果递归函数有个参数是i+1的话，则在递归层遍历中，取的值是不包含本身的下一个。

  比如1 2 3 4，横向层次取1时候下次层递归的时候

  1. i+1：应该选择2 3 4
  2. i：应该选择1 2 3 4

  横向层次取2的时候

  1. i+1: 应选择 3 4
  2. i：应选择 2 3 4

40. 组合总和 II

和47题条件一样，但是本质是属于求组合数的。

vector> res;
vector temp;
vector> combinationSum2(vector& candidates, int target) {
    int len = candidates.size();
    sort(candidates.begin(), candidates.end());
    vector is_used(len, false);
    back_tracing(candidates, target, len, 0, 0, is_used);
    return res;
}
void back_tracing(vector& candidates, int target, int len, int start, int sum, vector& is_used){
    if(sum == target){
        res.push_back(temp);
        return;
    }
    else if(sum > target){
        return;
    }
    for(int i = start; i < len; i++){
        //这道题和47题特别想，一个是排列一个是组合
        //关键就在于i=start还是i=1
        if(i > 0 && is_used[i-1]==false && candidates[i-1] == candidates[i]){
            continue;
        }
        temp.push_back(candidates[i]);
        is_used[i] = true;
        sum += candidates[i];
        back_tracing(candidates, target, len, i+1, sum, is_used);
        sum -= candidates[i];
        temp.pop_back();
        is_used[i] = false;            
    }

}

216. 组合总和 III

vector> res;
vector temp;
vector> combinationSum3(int k, int n) {
    vector num = {1,2,3,4,5,6,7,8,9};
    back_tracing(num, n ,k ,0, 0);
    return res;
}

void back_tracing(vector& num, int n, int k, int sum, int start){
    if(temp.size() == k && sum == n){
        res.push_back(temp);
        return;
    }
    else if(sum > n){
        return;
    }
    for(int i = start; i < num.size(); i++){
        temp.push_back(num[i]);
        sum += num[i];
        back_tracing(num, n, k, sum, i+1);
        sum -= num[i];
        temp.pop_back();
    }
}

跟40题很相似，基本一样，但是已经排好序了没有重复，所以不用考虑重复的问题。

分割问题

131. 分割回文串

这道题的思路不要太简单，主要有两个点：一个函数用来判断是否是回文，一个用来分割字符串。

vector tmp;
vector> res;
vector> partition(string s) {
    int len = s.size();
    back_tracing(s, len, 0);
    return res;

}

void back_tracing(string s, int len, int start){
    if(start >= len){
        res.push_back(tmp);
        return;
    }
    for(int i = start; i < len; i++){
        string tmp_str = s.substr(start, i-start+1);
        if(is_palindrome(tmp_str)){
            tmp.push_back(tmp_str);
        }else{
            //重要！！！
            continue;
        }
        back_tracing(s, len, i+1);
        tmp.pop_back();
    }
}

bool is_palindrome(string& str){
    int len = str.size();
    if(len == 1){
        return true;
    }
    int l = 0;
    int r = len - 1;
    while(l < r){
        if(str[l] == str[r]){
            l++;
            r--;
        }else{
            return false;
        }
    }
    return true;
}

• 涉及到的知识

  • 判断是否回文，有字符串，链表的。字符串的判断就是如上代码，一个while循环，一个从0开始，一个从最后一个位置索引开始，依次比较是否相等

  • 分割字符串，需要递归遍历，用到了回溯算法。这里面有几个值得注意的点

    • if中结束条件。这个题如果有满足的想加入到vector数组中，苦思冥想，不知道该什么时候加入。这道题给了我们思路，当遍历原始字符串长度大于的时候就结束了了！为啥等于呢，因为最后一位单个肯定是回文字符串

    • 截取子串是substt(pos, pos+count)，注意是[pos, pos+count]，包括两端。

      同时这个count是长度，所以在代码中表现为i - start +1。

(字节)93. 复原 IP 地址

跟上题分割回文串一样的思路，我们先分割字符串。但是ip地址一共有四个段，所以我们的temp数组只要存储有四段string字符串就可以开始判断，如果满足ip地址的要求就加入，不满足就return；

vector res;
vector tmp;
vector restoreIpAddresses(string s) {
    int len = s.size();
    back_tracing(s, len, 0);
    return res;
}
void back_tracing(string s, int len, int start){
    if(start == len && tmp.size() == 4){
        string str_ip = tmp[0];
        for(int i = 1; i < 4; i++){
            str_ip  = str_ip + "." + tmp[i];
        }
        res.push_back(str_ip);
        return;
    }
    if(start < len && tmp.size() == 4){
        return;
    }
    for(int i = start; i < len; i++){
        //分割子串，这里是重点！！！
        string str_tmp = s.substr(start , i - start + 1);
        if(!jarge(str_tmp)){
            break;
        }
        cout<<"str_tmp"< 1 && s[0] == '0'){
        return false;
    }
    int a = atoi(s.c_str());
    if(a > 255){
        return false;
    }
    return true;
}

• 存在的问题

  • 第一点是最开始我们用temp变量来存储分割出来满足ip的字符串，但是这会存在一个问题，当我们回溯的时候，不好去删除string temp之前加入进来的值，这个真的不好删除，特别不好写，所以这样不行。另外一个思路是用vector数组来存储，这样回溯的时候可以pop。

  • ip地址共有四段，但是第四段不好截取。因此我们就在if中判断，如果有三段之后，随后一段截取就很方便，如代码string last = s.substr(start, s.size() -1);如果last符合ip规则，我们temp数组就有四段，可以拼接到一起

    如果last不满足，则直接返回，temp数组回溯的时候也一次出来

  • for循环时候，还是要i+1，因为递归层不能重复取当前值，而是从下一个值开始取得

  • "111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111"这个回答会超时，记住要判定string长度大于13直接pass！

• c++知识点

  • 截取子串是substr(pos, pos+count)
  • string转换成int用的是stoi，但是切记stoi能转换的最大数组长度到10，因此要判断如果string长度大于10就直接返回，肯定不满足，当时一直在这个点报错。

子集问题

78. 子集

组合问题，分割问题都是关注叶子节点，而子集问题却要关注树的每个节点，都要遍历到。

同样不能出现重复，因此for循环从start开始

vector> res;
vector temp; 
vector> subsets(vector& nums) {
    back_tracing(nums, 0);
    return res;
}
void back_tracing(vector& nums, int start){
    res.push_back(temp);
    for(int i = start; i < nums.size(); i++){
        temp.push_back(nums[i]);
        back_tracing(nums, i+1);
        temp.pop_back();
    }
}

90. 子集 II

跟78题比较，主要是在去重上

vector> res;
vector temp;
vector> subsetsWithDup(vector& nums) {
    vector use_check(nums.size(), false);
    sort(nums.begin(), nums.end());
    back_tracing(nums, 0, use_check);
    return res;
}
void back_tracing(vector& nums, int start, vector& use_check){
    res.push_back(temp);
    for(int i = start; i  0 && nums[i] == nums[i-1] && use_check[i-1] == false){
            continue;
        }
        temp.push_back(nums[i]);
        use_check[i] = true;
        back_tracing(nums, i+1, use_check);
        temp.pop_back();
        use_check[i] = false;
    }
}

• 总结

  去重主要由两种：

  1. 不加use_check数组

      if(i > 0 && nums[i] == nums[i-1]){
          continue;
       }
     

     不加use_check数组的话，对于同一层元素，如果有重复我们就是不能用它，如下图：

     

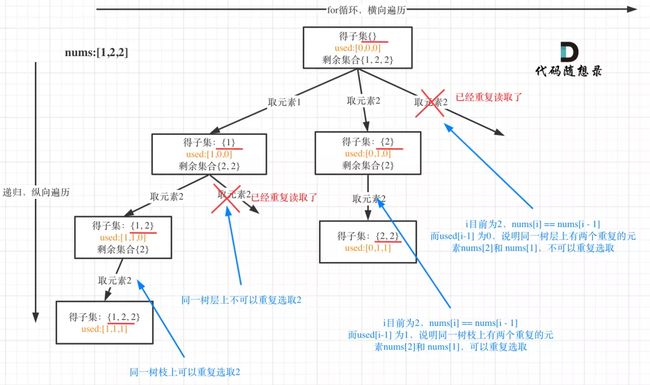
     对于同一树枝来说，第三层得自己[1 ,2]，第四层的[1, 2, 2]如果不加use_check数组，肯定得不到122这个数组,当if判断的时候就跳过了，但我们还要用到2，所以上述代码不合适。

  2. 加use_check数组

     if(i > 0 && nums[i] == nums[i-1] && use_check[i-1] == false){
          continue;
       }
     

     used[i - 1] == true，说明同一树支candidates[i - 1]使用过

     used[i - 1] == false，说明同一树层candidates[i - 1]使用过

     而我们要对同一树层使用过的元素进行跳过。