机器学习——聚类——密度聚类法——OPTICS

理论部分

1.1 提出背景

在DBSCAN算法中，需要人为确定领域半径$ϵ$和密度阈值$M$,同时该算法的性能又对这两个超参数非常敏感，不同的初始参数设定会导致完全不同的结果。基于此，学者们提出了新的聚类算法OPTICS。该聚类算法同样也是基于密度聚类的算法，与DBSCAN不同的是，该算法的设计使得其对初始超参数的设定敏感度较低。

1.2 OPTICS算法

1.2.1 基本概念

·核心距离
一个对象$p$的核心距离定义为使得其成为核心对象的最小距离，设$M$表示密度阈值，$N_{ϵ}(x)$表示以$x$为核心，$ϵ$为半径区域内的点构成的集合。$N_{ϵ}^i(x)$表示$N_{ϵ}(x)$中距离$x$第$i$近的点。则样本点$x$的核心对象可定义如下：
$$cd(x)=\{\begin{array}{rlr}Undefined& & if|N_{ϵ}(x)|<M\\ d(x,N_{ϵ}^M(x))& & if|N_{ϵ}(x)|\ge M\end{array}$$
可以看出：一个样本点必须首先是核心点，其核心距离才会有定义。假设$x$点为一个核心对象，找到以$x$点为圆心，且刚好满足密度阈值$M$的最外层的一个点,假设记为$x’$，则$x$点到$x’$点的距离称为核心距离。

·可达距离
可达距离的定义方式基于核心距离，对于一个核心点$x$,假设$x_i$为其周围的的点，如果$x$与$x_i$之间的距离大于$x$的核心距离，则其可达距离定义为两者间的实际距离，否则，定义为$x$的核心距离。即：
$$rd(y,x)=\{\begin{array}{rlr}Undefined& & if|N_{ϵ}(x)|<M\\ max(cd(x),d(x,y))& & if|N_{ϵ}(x)|\ge M\end{array}$$

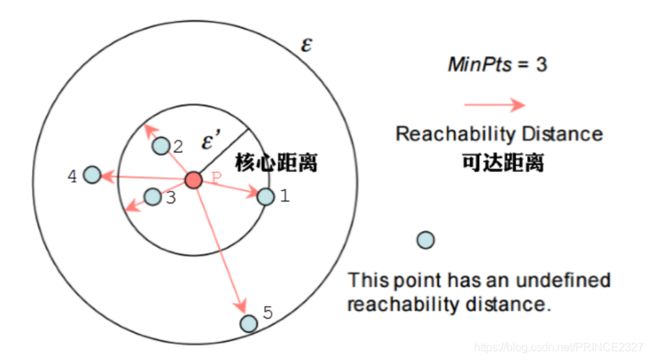
如上图所示，样本点$p$为核心点，样本点1，样本点，样本点3相对$p$的可达距离为$p$的核心距离，样本点4，样本点5相对$p$的可达距离为其到$p$的实际距离。

1.2.2 算法流程

输入：样本集D, 邻域半径ε, 给定点在ε领域内成为核心对象的最小领域点数MinPts
输出：具有可达距离信息的样本点输出排序

流程：
   1.创建两个队列，有序队列和结果队列。（有序队列用来存储核心对象及其该核心对象的密度直达对象，并按可达距离升序排列；结果队列用来存储样本点的输出次序。可以把有序队列里面放的理解为待处理的数据，而结果队列里放的是已经处理完的数据）。

   2.如果所有样本集D中所有点都处理完毕，则算法结束。否则，选择一个未处理（即不在结果队列中）且为核心对象的样本点，找到其所有密度直达样本点，如果该样本点不存在于结果队列中，则将其放入有序队列中，并按可达距离排序。

   3.如果有序队列为空，则跳至步骤2（重新选取处理数据）。否则，从有序队列中取出第一个样本点（即可达距离最小的样本点）进行拓展，并将取出的样本点保存至结果队列中(如果它不存在结果队列当中的话)。然后进行下面的处理：
      （1）.判断该拓展点是否是核心对象，如果不是，回到步骤3（因为它不是核心对象，所以无法进行扩展了。那么就回到步骤3里面，取最小的。这里要注意，第二次取不是取第二小的，因为第一小的已经放到了结果队列中了，所以第二小的就变成第一小的了。）。如果该点是核心对象，则找到该拓展点所有的密度直达点。

      （2）.判断这些密度直达样本点是否已经存在结果队列，是则不处理，否则下一步。

      （3）.如果有序队列中已经存在该直接密度可达点，如果此时新的可达距离小于旧的可达距离，则用新可达距离取代旧可达距离，有序队列重新排序(因为一个对象可能直接由多个核心对象可达，因此，可达距离近的肯定是更好的选择)。

      （4）.如果有序队列中不存在该密度直达样本点，则插入该点，并对有序队列重新排序。

   4.迭代2，3。

   5.算法结束，输出结果队列中的有序样本点。

以流程图的方式展示如下：

·D: 待聚类的集合
·Q: 有序队列，元素按照可达距离排序，可达距离最小的在队首
·O: 结果队列，最后输出结果的点集的有序队列

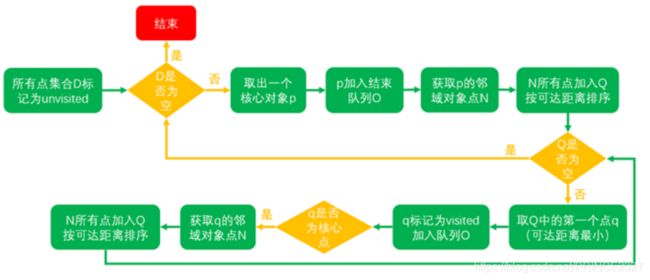
得到结果队列后，使用如下算法得到最终的聚类结果：

·从结果队列中按顺序取出点，如果该点的可达距离不大于给定半径ε，则该点属于当前类别，否则至步骤2。
·如果该点的核心距离大于给定半径ε，则该点为噪声，可以忽略，否则该点属于新的聚类，跳至步骤1。
·结果队列遍历结束，则算法结束。
上面的算法处理完后，我们得到了输出结果序列，每个节点的可达距离和核心距离。我们以可达距离为纵轴，样本点输出次序为横轴进行可视化：

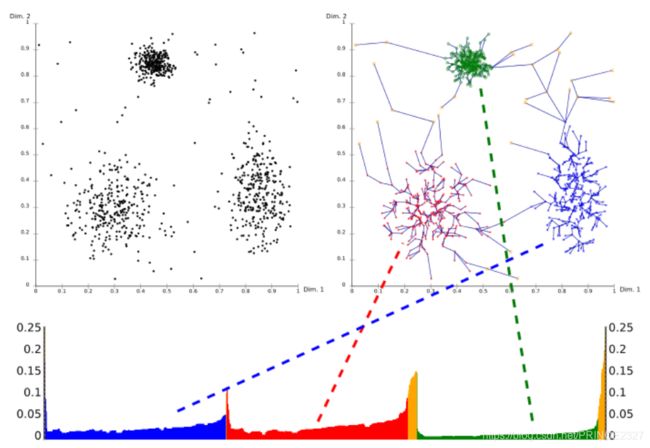
其中：

·X轴代表OPTICS算法处理点的顺序，Y轴代表可达距离。
·簇在坐标轴中表述为山谷，并且山谷越深，簇越紧密
·黄色代表的是噪声，它们不形成任何凹陷。

当需要提取聚集的时候，参考Y轴和图像，设定一个阀值就可以提取聚集了：

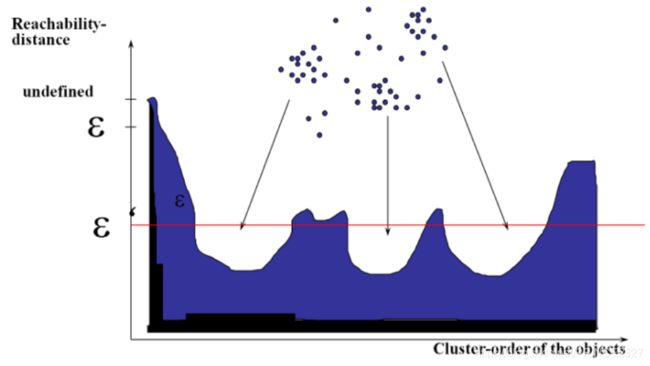
简而言之：OPTICS算法在特定参数情况下将每一个簇中的点按照可达距离排序从而输出，在计算样本点可达距离的过程中，从一个核心点开始并找出其$ϵ$中所有点，并依次计算这些点关于该核心点的核心距离，并且进行排序，如果其$ϵ$领域点中存在核心点，则找出新$ϵ$领域中所有样本点，并计算这些样本点关于新核心点的可达距离，而后进行排序。如果这些新$ϵ$领域内的某个样本点在旧$ϵ$领域中已经存在，则该样本点的可达距离定义为该样本点关于两个核心点的可达距离中较小的那个。以此类推，这样，在一个簇中，我们可以看到可达距离上升的排列。当第一个簇的某一个核心点的$ϵ$领域中不再存在核心点，则表明此时已经到达该簇的边界。下面就该选取下一个核心点，该核心点标志着另一个簇的开始，所以OPTICS输出结果的曲线中可以看到在到达最高点后又急速下降至较低点的趋势，这表明另一个密集簇的开始，和第一个簇的处理流程一样，处理完每一个簇，便可得到输出曲线。

OPTICS的核心思想：

·较稠密簇中的对象在簇排序中相互靠近
·一个对象的最小可达距离给出了一个对象连接到一个稠密簇的最短路径（这也就是为什么一个样本点的可达距离定义为它关于各个核心距离中最小的那一个）

1.2.3 优点

1.相对于DBSCAN，该算法对于距离阈值$ϵ$的敏感性大大降低，这是因为：

（1）.在OPTICS算法中从输出得到的并不是直接的聚类结果，而是在$ϵ$和$M$下的有序队列，以及所有样本点的核心距离和可达距离。

（2）.在处理结果队列O时，通过判断样本点的核心距离是否小于等于$ϵ$实际上就是在判断该样本点是否是新半径${ϵ}^{{}^{\prime }}$的核心点，其中${ϵ}^{{}^{\prime }}<ϵ$。而两者都不满足的样本点一定会被认为是噪声，所以对于距离阈值，该算法有一定的不敏感性。

2.OPTICS相当于将$ϵ$改为动态的DBSCAN算法，可以进行多密度的聚类（因为$ϵ$对于结果的影响较低，且输出中包含了关于可达距离的信息，可以辅助设置$ϵ$)

综上所述，OPTICS可以在minPts固定的前提下，对于任意的ε’ (其中ε’小于等于ε)都可以直接经过简单的计算得到新的聚类结果。

PS：直观从结果图来看，以某一个可达距离$ϵ$话平行于$x$轴的直线，当直线穿过几个山谷区域，最终就会得到几种簇（因为每一个山谷代表一种簇，或说一团高密度区域）。在此基础上，我们可以选择合适的可达距离$ϵ$做为其它距离算法（例如DBSCAN）的初始参数设定从而进行聚类。从这个角度来看，OPTICS聚类算法也可以被认为是一种筛选最优距离阈值$ϵ$的方法，如下图：

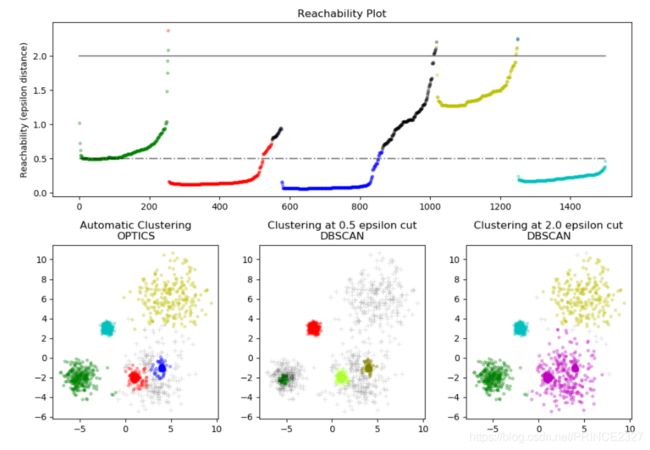
当然，也可以不使用其它算法进行最后聚类的结果。可以根据可达距离-处理顺序图所得到的结果设置一个斜率阈值，在读可达距离-处理顺序图的曲线时，当读到斜率大于斜率阈值的部分时，就代表新建一个聚类簇（因为斜率较大代表可达距离增长迅速，也代表该点里上一个聚类中心逐渐变远），如此也可以得到聚类结果。

要注意的是，基于DBSCAN去得到最终结果和直接基于斜率阈值去得到最终结果尽管非常相似，但并不是完全相同的，这是因为由OPTICS处理的每个密集区域的第一个样本具有大的可达性值，使得接近其区域中的其他点，因此有时将被标记为噪声。当它们被视为噪声的候选点时，这会影响相邻点的判断。

1.2.4 缺点

1.由OPTICS处理的每个密集区域的第一个样本具有大的可达性值，使得接近其区域中的其他点，因此有时将被标记为噪声。当它们被视为噪声的候选点时，这会影响相邻点的判断。

1.3 其它算法

基于OPTICS算法扩展有很多，比如：

   1.OPTICS-OF用来检测异常值(Outliar Detection)
   2.DeLi-Clu算法来消除eps参数，提供比OPTICS更好的性能指标
   3.HiSC算法将其应用到Subspace Clustering
   4.HiCO应用到相关聚类(Correlation Clustering)上
   5.基于HiSC改进的DiSH能够找到更加复杂的簇结构

代码部分

2.1 自行实现

# -*- coding: gbk -*-

import numpy as np
import matplotlib.pyplot as plt
import copy
from sklearn.datasets import make_moons
from sklearn.datasets.samples_generator import make_blobs
import random
import time


class OPTICS():
    def __init__(self, epsilon, MinPts):
        self.epsilon = epsilon
        self.MinPts = MinPts

    def dist(self, x1, x2):
        return np.linalg.norm(x1 - x2)

    def getCoreObjectSet(self, X):
        N = X.shape[0]
        Dist = np.eye(N) * 9999999
        CoreObjectIndex = []
        for i in range(N):
            for j in range(N):
                if i > j:
                    Dist[i][j] = self.dist(X[i], X[j])
        for i in range(N):
            for j in range(N):
                if i < j:
                    Dist[i][j] = Dist[j][i]
        for i in range(N):
            # 获取对象周围小于epsilon的点的个数
            dist = Dist[i]
            num = dist[dist < self.epsilon].shape[0]
            if num >= self.MinPts:
                CoreObjectIndex.append(i)
        return np.array(CoreObjectIndex), Dist

    def get_neighbers(self, p, Dist):
        N = []
        dist = Dist[p].reshape(-1)
        for i in range(dist.shape[0]):
            if dist[i] < self.epsilon:
                N.append(i)
        return N

    def get_core_dist(self, p, Dist):
        dist = Dist[p].reshape(-1)
        sort_dist = np.sort(dist)
        return sort_dist[self.MinPts - 1]

    def resort(self):
        '''
        根据self.ReachDist对self.Seeds重新升序排列
        '''
        reachdist = copy.deepcopy(self.ReachDist)
        reachdist = np.array(reachdist)
        reachdist = reachdist[self.Seeds]
        new_index = np.argsort(reachdist)
        Seeds = copy.deepcopy(self.Seeds)
        Seeds = np.array(Seeds)
        Seeds = Seeds[new_index]
        self.Seeds = Seeds.tolist()

    def update(self, N, p, Dist, D):

        for i in N:
            if i in D:
                new_reach_dist = max(self.get_core_dist(p, Dist), Dist[i][p])
                if i not in self.Seeds:
                    self.Seeds.append(i)
                    self.ReachDist[i] = new_reach_dist
                else:
                    if new_reach_dist < self.ReachDist[i]:
                        self.ReachDist[i] = new_reach_dist
                self.resort()

    def fit(self, X):
        length = X.shape[0]
        CoreObjectIndex, Dist = self.getCoreObjectSet(X)
        self.Seeds = []
        self.Ordered = []
        D = np.arange(length).tolist()
        self.ReachDist = [-0.1] * length

        while (len(D) != 0):
            p = random.randint(0, len(D) - 1)  # 随机选取一个对象
            p = D[p]
            self.Ordered.append(p)
            D.remove(p)

            if p in CoreObjectIndex:
                N = self.get_neighbers(p, Dist)
                #print(N)
                self.update(N, p, Dist, D)

                while(len(self.Seeds) != 0):
                    q = self.Seeds.pop(0)
                    self.Ordered.append(q)
                    D.remove(q)
                    if q in CoreObjectIndex:
                        N = self.get_neighbers(q, Dist)
                        self.update(N, q, Dist, D)
        #print(self.Seeds,self.ReachDist[:20])
        return self.Ordered, self.ReachDist

    def plt_show(self, X, Y, ReachDist, Ordered, name=0):
        if X.shape[1] == 2:
            fig = plt.figure(name)
            plt.subplot(211)
            plt.scatter(X[:, 0], X[:, 1], marker='o', c=Y)
            plt.subplot(212)
            ReachDist = np.array(ReachDist)
            print(Ordered)
            plt.plot(range(len(Ordered)), ReachDist[Ordered])
        else:
            print('error arg')


if __name__ == '__main__':
    # 111111
    center = [[1, 1], [-1, -1], [1, -1]]
    cluster_std = 0.35
    X1, Y1 = make_blobs(n_samples=300, centers=center,
                        n_features=2, cluster_std=cluster_std, random_state=1)
    optics1 = OPTICS(epsilon=2, MinPts=5)
    Ordered, ReachDist = optics1.fit(X1)
    optics1.plt_show(X1, Y1, ReachDist, Ordered, name=1)

结果如下：

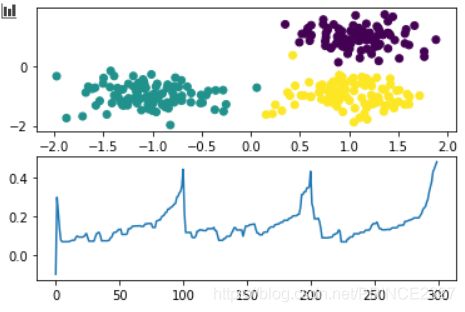
可在该结果的基础上选取合适的参数再应用例如DBSCAN的算法进行聚类。

2.2 sklearn实现

from sklearn.cluster import OPTICS, cluster_optics_dbscan
import matplotlib.gridspec as gridspec
import matplotlib.pyplot as plt
import numpy as np

# Generate sample data

np.random.seed(0)
n_points_per_cluster = 250

C1 = [-5, -2] + .8 * np.random.randn(n_points_per_cluster, 2)
C2 = [4, -1] + .1 * np.random.randn(n_points_per_cluster, 2)
C3 = [1, -2] + .2 * np.random.randn(n_points_per_cluster, 2)
C4 = [-2, 3] + .3 * np.random.randn(n_points_per_cluster, 2)
C5 = [3, -2] + 1.6 * np.random.randn(n_points_per_cluster, 2)
C6 = [5, 6] + 2 * np.random.randn(n_points_per_cluster, 2)
X = np.vstack((C1, C2, C3, C4, C5, C6))

clust = OPTICS(min_samples=50, xi=.05, min_cluster_size=.05)

# Run the fit
clust.fit(X)

labels_050 = cluster_optics_dbscan(reachability=clust.reachability_,
                                   core_distances=clust.core_distances_,
                                   ordering=clust.ordering_, eps=0.5)
labels_200 = cluster_optics_dbscan(reachability=clust.reachability_,
                                   core_distances=clust.core_distances_,
                                   ordering=clust.ordering_, eps=2)

space = np.arange(len(X))
reachability = clust.reachability_[clust.ordering_]
labels = clust.labels_[clust.ordering_]

plt.figure(figsize=(10, 7))
G = gridspec.GridSpec(2, 3)
ax1 = plt.subplot(G[0, :])
ax2 = plt.subplot(G[1, 0])
ax3 = plt.subplot(G[1, 1])
ax4 = plt.subplot(G[1, 2])

# Reachability plot
colors = ['g.', 'r.', 'b.', 'y.', 'c.']
for klass, color in zip(range(0, 5), colors):
    Xk = space[labels == klass]
    Rk = reachability[labels == klass]
    ax1.plot(Xk, Rk, color, alpha=0.3)
ax1.plot(space[labels == -1], reachability[labels == -1], 'k.', alpha=0.3)
ax1.plot(space, np.full_like(space, 2., dtype=float), 'k-', alpha=0.5)
ax1.plot(space, np.full_like(space, 0.5, dtype=float), 'k-.', alpha=0.5)
ax1.set_ylabel('Reachability (epsilon distance)')
ax1.set_title('Reachability Plot')

# OPTICS
colors = ['g.', 'r.', 'b.', 'y.', 'c.']
for klass, color in zip(range(0, 5), colors):
    Xk = X[clust.labels_ == klass]
    ax2.plot(Xk[:, 0], Xk[:, 1], color, alpha=0.3)
ax2.plot(X[clust.labels_ == -1, 0], X[clust.labels_ == -1, 1], 'k+', alpha=0.1)
ax2.set_title('Automatic Clustering\nOPTICS')

# DBSCAN at 0.5
colors = ['g', 'greenyellow', 'olive', 'r', 'b', 'c']
for klass, color in zip(range(0, 6), colors):
    Xk = X[labels_050 == klass]
    ax3.plot(Xk[:, 0], Xk[:, 1], color, alpha=0.3, marker='.')
ax3.plot(X[labels_050 == -1, 0], X[labels_050 == -1, 1], 'k+', alpha=0.1)
ax3.set_title('Clustering at 0.5 epsilon cut\nDBSCAN')

# DBSCAN at 2.
colors = ['g.', 'm.', 'y.', 'c.']
for klass, color in zip(range(0, 4), colors):
    Xk = X[labels_200 == klass]
    ax4.plot(Xk[:, 0], Xk[:, 1], color, alpha=0.3)
ax4.plot(X[labels_200 == -1, 0], X[labels_200 == -1, 1], 'k+', alpha=0.1)
ax4.set_title('Clustering at 2.0 epsilon cut\nDBSCAN')

plt.tight_layout()
plt.show()