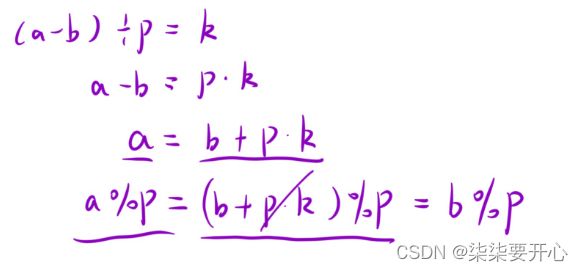【算法刷题】Day23
文章目录
- 1. 打家劫舍 II
-
- 题干：
- 算法原理：（dp）
-
- 1. 状态表示：
- 2. 状态转移方程
- 3. 初始化
- 4. 填表顺序
- 5. 返回值
- 代码：
- 2. 和为 K 的子数组
-
- 题干：
- 算法原理：
-
- 1. 暴力枚举
- 2. 前缀和 + 哈希表
- 代码：
- 3. 和可被 K 整除的子数组
-
- 题干：
- 算法原理：（前缀和）
- 代码：
1. 打家劫舍 II
原题链接
题干：
所有的房屋都 围成一圈
如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警
偷窃到的最高金额
算法原理：（dp）
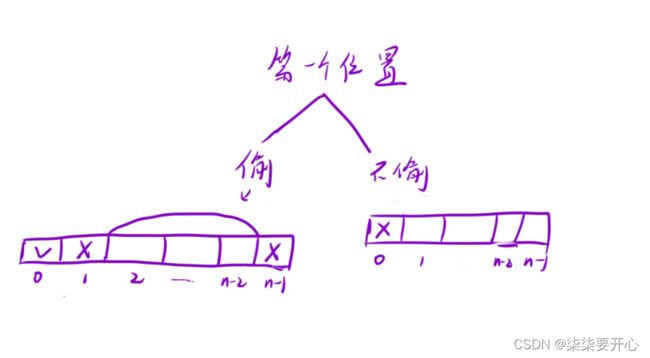
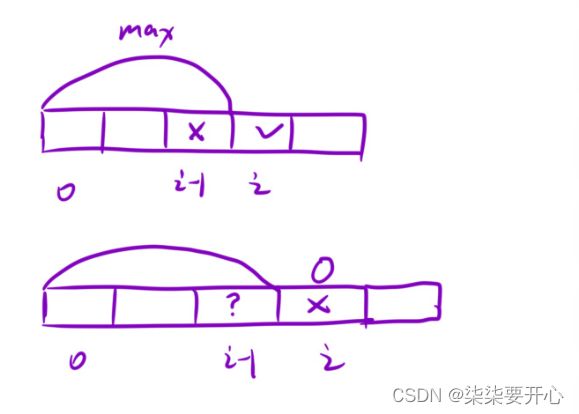
对于第一个位置有两种情况
在偷的情况下，第二个位置 和 倒数第二个位置都不能偷
在不偷的情况下，后面的就跟昨天的按摩师一样
偷：nums[0] + rob1(2, n-2)
不偷：rob1(1, n-1)
因此，环形问题就转化成求「两次单排结果的最大值」
1. 状态表示：
f[i] 表示：偷到 i 位置时，偷 nums[i]，此时的最大金额
g[i] 表示：偷到 i 位置时，不偷 nums[i]，此时的最大金额
2. 状态转移方程
f[i] = g[i - 1] + nums[i]
g[i] = max(f[i - 1], g[i- 1])
3. 初始化
f[0] = nums[0]
g[0] = 0
4. 填表顺序
从左往右，两个表⼀起填
5. 返回值
max(f[n - 1], g[n - 1])
代码：
class Solution {
public int rob(int[] nums) {
int n = nums.length;
return Math.max(rob1(nums, 2, n - 2) + nums[0], rob1(nums, 1, n - 1));
}
public int rob1(int[] nums,int left,int right) {
if(left > right) {
return 0;
}
int n = nums.length;
int[] f = new int[n];
int[] g = new int[n];
f[left] = nums[left];
for(int i = left + 1; i <= right; i++) {
f[i] = g[i - 1] + nums[i];
g[i] = Math.max(f[i - 1], g[i - 1]);
}
return Math.max(f[right], g[right]);
}
}
2. 和为 K 的子数组
原题链接
题干：
返回 该数组中和为 k 的子数组的个数
-1000 <= nums[i] <= 1000
算法原理：
1. 暴力枚举
将所有的子数组求一遍
然后进行返回
优化：
这里不可以使用双指针优化
因为有负数的原因，中间的可能会出现相加为 0 的情况
这样就不能使用双指针了，因为不具有单调性
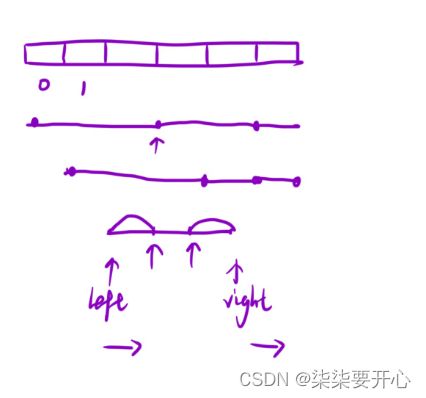
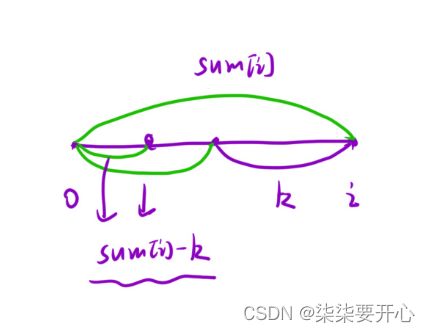
2. 前缀和 + 哈希表
引入 以 i 为结尾的所有的子数组
这样就可以转化为：
在 [0,i-1] 区间内，有多少个前缀和 等于 sum[i] - k
这样就可以使用哈希表
细节问题：
- 前缀和加入哈希表的时机
在计算 i 位置之前，哈希表里面只保存 [0,i-1] 位置的前缀和 - 不用真的创建一个前缀和数组
用一个变量 sum 来标记前一个位置的前缀和即可
dp[i] = sum + nums[i] - 如果整个前缀和等于 k 呢？
这个时候先让 hash[0] = 1 即可
代码：
class Solution {
public int subarraySum(int[] nums, int k) {
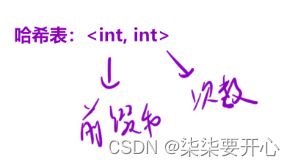
Map<Integer, Integer> hash = new HashMap<Integer, Integer>();
hash.put(0,1);
int sum = 0;
int ret = 0;
for(int x : nums) {
sum += x;//计算当前的前缀和
ret += hash.getOrDefault(sum - k, 0);//统计结果
hash.put(sum, hash.getOrDefault(sum, 0) + 1);//把当前的前缀和放入哈希表
}
return ret;
}
}
3. 和可被 K 整除的子数组
原题链接
题干：
返回其中元素之和可被 k 整除的（连续、非空） 子数组 的数目
这道题和上一题非常相似
算法原理：（前缀和）
这里我们先引入两个数学原理
（1）同余定理
如果：(a - b) / p = k…0
就可以说明：a % k = b % k
并且 (a + p*k) % p = a % p
证明：
（2）对于[负数 % 正数] 的结果进行修正
在 java 中 负数 % 正数是等于负数
我们要想进行修正成为正数
为了正负统一：(a % p + p) % p
接下来，就可以来进行前缀和的思想解题了
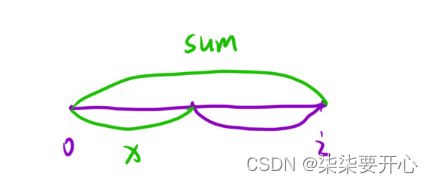
(sum - x) % k = 0
就可以变为：sum % k = x % k
这样就可以转化为：
在 [0,i-1] 区间内，找到有多少个前缀和的余数等于 (sum % k + k) % k
代码：
class Solution {
public int subarraysDivByK(int[] nums, int k) {
Map<Integer, Integer> hash = new HashMap<Integer, Integer>();
hash.put(0 % k, 1);
int sum = 0;
int ret = 0;
for(int x : nums) {
sum += x;
int r = (sum % k + k) % k;
ret += hash.getOrDefault(r, 0);
hash.put(r, hash.getOrDefault(r, 0) + 1);
}
return ret;
}
}
