matlab实验一 图像增强
实验一 图像增强
-
- 一、实验目的
- 二、实验环境
- 三、相关函数
- 四、实验内容:
-
- 一 . 灰度变换
- 二 . 空域滤波
- 三.频域增强
一、实验目的
- 熟悉及掌握图像的灰度转换。
- 理解直方图的概念及应用,实现图像直方图的显示,及通过直方图均衡化方法对图像进行修正。
- 熟悉并掌握平滑空间滤波器;
- 熟悉并掌握锐化空间滤波器。
- 熟悉及掌握图像的变换原理及性质,实现图像的傅里叶变换。
- 理解并掌握常用的图像频域增强技术。
二、实验环境
MATLAB R2010b版本、WIN 7计算机
三、相关函数
-
imwrite(): 用于写入图像文件如:imwrite(a,‘e:\w02.tif’,’tif’)
-
plot(): 绘制二维图形 plot(y),plot(x,y), x y可以是向量、矩阵。
-
imresize(): 改变图像矩阵的维度,如:I=imresize(j,[m n])将图像j大小调整为m行n列。
-
imhist():用于数字图像的直方图计算或显示,如imhist(I, n)计算和显示图像I的直方图,n为指定的灰度级数目,默认为256。如果I是二值图像,那么n仅有两个值。
如: i=imread(‘e:\w01.tif’); imhist(i); -
histeq(): 用于数字图像的直方图均衡化,J = histeq(I, n) 均衡化后的级数n,缺省值为64。J = histeq(I, hgram) “直方图规定化”,即将原是图象 I 的直方图变换成用户指定的向量 hgram (即指定另一幅图像的直方图数据向量)。
-
imadjust(): 用于数字图像的灰度或颜色调整,如:
J = imadjust(I,[low_in,igh_in],[low_out,high_out]) 将图像I中的亮度值映射到J中的新值,即将low_in至high_in之间的值映射到low_out至high_out之间的值。low_in 以下与 high_in 以上的值被剪切掉了,也就是说,low_in 以下的值映射到 low_out,high_in 以上的值映射到high_out。它们都可以使用空的矩阵[],默认值是[0 1]。 如:
j=imadjust(i,[0.3,0.7],[]);将图像i转换为j,使灰度值从0.3~0.7与缺省值0-1相匹配 -
im2double():参数为unit8型数组时,转化结果矩阵元素取值位于(0,1)。但im2double()的参数是double型时,直接输出参数本身,不做任何数值类型和数值大小的处理。
-
double():参数为unit8型数组时,转化结果矩阵元素取值位于(0,255)
-
covn2(): 计算两个矩阵的二维卷积。
C = conv2(A,B)
若A为ma×na的矩阵,B为mb×nb的矩阵,则C的大小为(ma+mb-1)×(na+nb-1)。 -
filter2():计算二维线型数字滤波,它与函数 fspecial 连用搜索
Y=filter2(B,X)
Y=filter2(B,X,‘shape’)
说明:对于 Y=filter2(B,X) ,filter2 使用矩阵 B 中的二维 FIR 滤波器对数据 X 进行滤波,结果 Y 是通过二维相关计算出来的,其大小与 X 一样;对于 Y=filter2(B,X,‘shape’) ,filter2 返回的 Y 是通过二维互相关计算出来的,其大小由参数 shape 确定,其取值如下: -
fspecial():用于建立预定义的滤波算子。
h = fspecial(type)
h = fspecial(type,para)
其中type指定算子的类型,para指定相应的参数; -
Imfilter():实现线性空间滤波函数
功能:对任意类型数组或多维图像进行滤波。
数语法:g=imfilter(f,w,filtering_mode,boundary_options,size_optinos)
参数介绍:f是输入图像,w为滤波模板,g为滤波结果;表1-1总结了其他参数的含义。v -
fft2
fft2函数用于数字图像的二维傅立叶变换,如
j=fft2(i)
由于MATLAB无法显示复数图像,因此变换后的结果还需进行求模运算,即调用abs函数。 -
F=abs(j)
之后常常还进行对数变换,即调用log函数,以减缓傅里叶谱的快速衰减,更好地显示高频信息。 -
ifft2
ifft2函数用于数字图像的二维傅立叶反变换,如:
k=ifft2(j); -
fftshift
圆周位移的操作。fftshift是将数组或矩阵按正方向(向右和向下)做圆周位移,用于将变换后图像频谱中心从矩阵的原点移动到矩阵的中心
B=fftshift(j); -
ifftshift
是按负方向(向左和向上)做圆周位移。圆周位移的步长等于数组或矩阵长度的一半 -
lpfilter
频域低通滤波函数,语法格式为:
H=lpfilter(type,M,N,D0,n);
Type:滤波器类型,包括(ideal,btw,gaussian)
M,N:输入图像大小
D0:截止半径
n:阶数 -
hpfilter
频域高通滤波函数,语法格式为:
H=hpfilter(type,M,N,D0,n);
Type:滤波器类型,包括(ideal,btw,gaussian)
M,N:输入图像大小
D0:截止半径
n:阶数

四、实验内容:
一 . 灰度变换
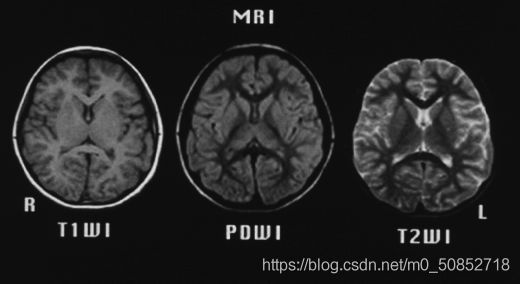
a) 将图像拆分为大小相等的t1,t2,pd三幅图像(拆分图像:图像总宽度为520,分成三等分,则每张图宽173个像素,还剩下一个边缘像素,略去),去掉图像中的文字,填充成背景色(灰度值为0)。
A=rgb2gray(imread('C:\pictures of QQshiyan\MRI脑图像.bmp')); %读取图片文件
figure;imshow(A);
%% 定标
hp = impixelinfo;
A(192:284,22:38)=0;
A(221:284,53:458)=0;
A(202:284,468:491)=0;
A(4:32,227:285)=0;
A1=A(1:284,1:170);
A2=A(1:284,170:340);
A3=A(1:284,340:520);
figure(1);
subplot(131);
imshow(A1);
title('T1w1')
subplot(132);
imshow(A2);
title('PDW1')
subplot(133);
imshow(A3);
title('T2W1');
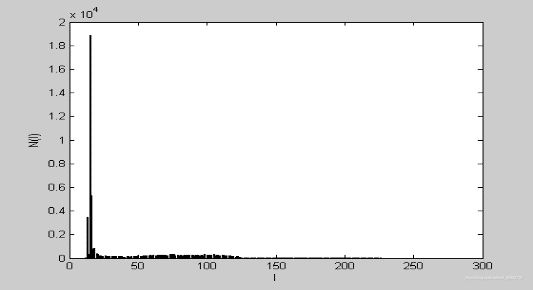
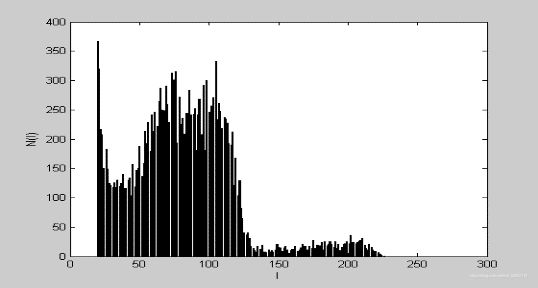
b) 分别绘出t1,t2,pd三幅图像去除背景前,和去除背景后(灰度<20)的灰度直方图。分析该操作的意义(写入实验报告)
B1=imhist(A1); %获取灰度直方图矩阵
B2=imhist(A2);
B3=imhist(A3);
figure(2); %作图
subplot(231);
stem(B1,'.');
title('未经处理的T1加权象直方图');
subplot(232);
stem(B2,'.');title('未经处理的PD加权象直方图');
subplot(233);
stem(B3,'.');title('未经处理的T2加权象直方图');
B1(1:20)=0; %去除灰度小于20的部分
B2(1:20)=0;
B3(1:20)=0;
subplot(234);
stem(B1,'.');title('去除背景(灰度<20)后T1加权象直方图');
subplot(235);
stem(B2,'.');title('去除背景(灰度<20)后T1加权象直方图');
subplot(236);
stem(B3,'.');title('去除背景(灰度<20)后T1加权象直方图');
未经处理的T1加权象直方图
去除背景(灰度<20)后T1加权象直方u图
c) 将pd图像(pdwi)进行直方图均衡化,显示结果。
J=histeq(A2);
figure(3);
subplot(2,2,1)
imshow(A2);title('PDW1')
subplot(2,2,2)
imshow(J);title('直方图均衡化PDW1')
subplot(2,2,3)
imhist(A2);title('未经处理的PD加权象直方图');
subplot(2,2,4)
imhist(J);title('均衡化的PD加权象直方图');
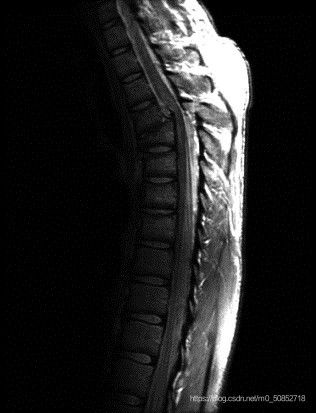
% 1. 实现幂律变换(幂次变换)
imggray = imread('C:\pictures of QQshiyan\脊椎骨MRI.tif'); %读取图象
figure('Name', '对比a数值实现幂律变换'); %设置标题
subplot(221);
imshow(imggray);%显示灰度图
title('原始灰度图像');
I = imadjust(imggray,[0 1],[0 1],0.3);%a值为0.3
subplot(222);
imshow(I);
title('a值为0.3灰度图像');
J = imadjust(imggray,[0 1],[0 1],0.8);%a值为0.8
subplot(223);
imshow(J);
title('a值为0.8灰度图像');
K = imadjust(imggray,[0 1],[0 1],1.7);%a值为1.7
subplot(224);
imshow(K);
title('a值为1.7灰度图像');
二 . 空域滤波
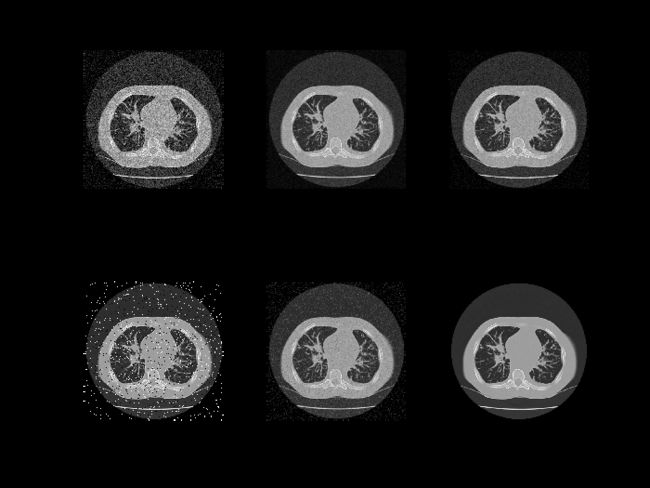
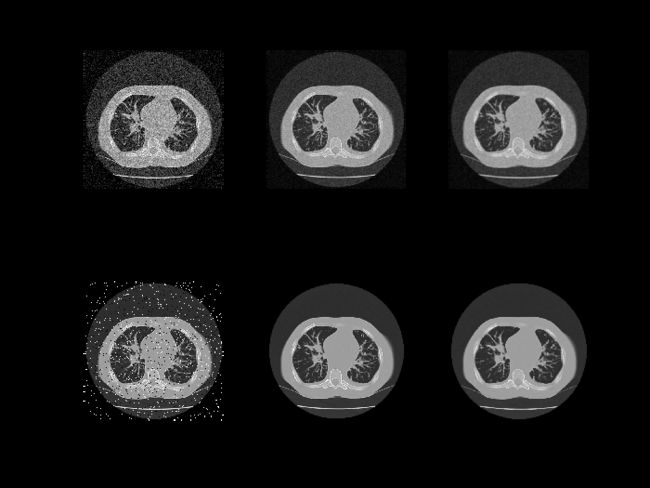
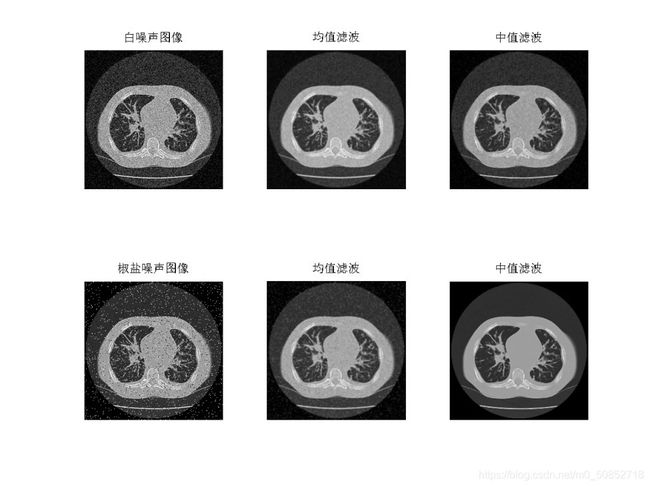
- 对含有高斯白噪声的图像(feiCT)和含有椒盐噪声的图像(feiCT2)分别采用不同大小的模板进行均值滤波,和中值滤波,用一个图像处理对话框显示原图像、均值滤波的图像及中值滤波的图像。
通过比较结果总结哪种滤波器适用于什么样的噪声并比较结果得出最优的模板大小。
I=imread('C:\pictures of QQshiyan\feiCT.tiff'); imshow(I);
J = imread('C:\pictures of QQshiyan\feiCT2.tiff'); imshow(J);
ave1=fspecial('average',3); %产生3×3的均值模版
ave2=fspecial('average',5); %产生5×5的均值模版
K = filter2(ave1,I)/255; %均值滤波3×3
L = filter2(ave1,J)/255; %均值滤波3×3
M = medfilt2(I,[3 3]); %中值滤波3×3模板
N = medfilt2(J,[3 3]); %中值滤波3×3模板
figure
subplot(2,3,1),imshow(I),title('feiCT');
subplot(2,3,4),imshow(J),title('feiCT2');
subplot(2,3,2),imshow(K),title('feiCT均值滤波3×3 ');
subplot(2,3,5),imshow(L),title('feiCT2均值滤波3×3 ');
subplot(2,3,3),imshow(M),title('feiCT中值滤波3×3模板');
subplot(2,3,6),imshow(N),title('feiCT2中值滤波3×3模板');
I=imread('C:\pictures of QQshiyan\feiCT.tiff'); imshow(I);
J = imread('C:\pictures of QQshiyan\feiCT2.tiff'); imshow(J);
ave1=fspecial('average',3); %产生3×3的均值模版
ave2=fspecial('average',5); %产生5×5的均值模版
K = filter2(ave1,I)/255; %均值滤波3×3
L = filter2(ave2,I)/255; %均值滤波5×5
M = medfilt2(J,[3 3]); %中值滤波3×3模板
N = medfilt2(J,[5 5]); %中值滤波5×5模板
figure
subplot(2,3,1),imshow(I),title('feiCT');
subplot(2,3,4),imshow(J),title('feiCT2');
subplot(2,3,2),imshow(K),title('feiCT均值滤波3×3 ');
subplot(2,3,3),imshow(L),title('feiCT均值滤波5×5 ');
subplot(2,3,5),imshow(M),title('feiCT2中值滤波3×3模板');
subplot(2,3,6),imshow(N),title('feiCT2中值滤波5×5模板');
中值滤波适用于椒盐噪声,均值滤波适用于白噪声,通过对比均值滤波器5×5模板,中值滤波器3×3模板为最优。
分析:
椒盐噪声用中值滤波比较好的原因是:
椒盐噪声是幅值近似相等但是随机的分布在不同位置,图中既有污染的点,也有干净的点。因为噪声的均值不为零,所以不适合均值滤波。图中有干净的点也有污染的点,所以中值滤波可以用干净的点代替污染的点。当然,中值滤波也有缺点:对于点、线、尖顶的图像不适用中值滤波因为会出现自适应话。
高斯噪声用均值滤波比较好的原因是:
高斯噪声的幅值近似正态分布,但是分布在每个点上。因为所有的点都被污染所以不能中值滤波选不到正确的干净的点。因为高斯噪声服从正态分布所以均值噪声为零可以选用均值滤波处理噪声
- 对图像’nao.png’分别采用H1和H2 'laplacian’高通滤波器进行锐化滤波,并得出拉普拉斯图像(标定前和标定后的),增强的图像,模板 H1=[0 1 0;1 -4 1;0 1 0],H2=[1 1 1;1 -8 1;1 1 1],比较结果,分析出现的问题及原因。
clc;clear all;close all;
%% 提取模板
H1=[0 1 0;1 -4 1;0 1 0];
H2=[1 1 1;1 -8 1;1 1 1];
%% 处理
I=imread('C:\pictures of QQshiyan\nao.jpg'); %读取图像
[ROW,COL, DIM] = size(I);%保存图像尺寸
subplot(231),imshow(I),title('原始图像');%显示原始图像
%A=fspecial('laplacian'); %生成系统预定义的3X3滤波器
Laplacian_img1=imfilter(I,H1);
subplot(232),imshow(Laplacian_img1),title('Laplacian算子H1');
Laplacian_img2=imfilter(I,H2);
subplot(233),imshow(Laplacian_img2),title('Laplacian算子 H2');
subplot(2,3,5);
im2=I+Laplacian_img1;
imshow(im2),title('H1锐化后图像');
subplot(2,3,6);
im3=I+Laplacian_img2;
imshow(im3),title('H2锐化后图像');
根据显示a)原始图像b)未标定的Laplacian算子H1滤波后的图像c)未标定的Laplacian算子H2滤波后的图像e)标
问题:1)边缘加粗2)出现椒盐噪声,且H2噪声比H1噪声强烈
原因:由于laplace图像支配特性是边缘和灰度不连续处,经拉普拉斯变换增强了图像中灰度图变出的对比度,消减图像模糊、突出目标边界与图像细节,但同时也增强了噪声(椒盐噪声)。标定后图像是原始图像和拉普拉斯图像相叠加,既能保护拉普拉斯锐化处理的效果,同时又能复原背景信息,用拉普拉斯变换突出图像小细节但会造成边缘加粗,灰度对比度增强,使得灰度突变处变成椒盐噪声,且拉普拉斯算子中心系数越大,锐化效果越明显,噪声越明显。
三.频域增强
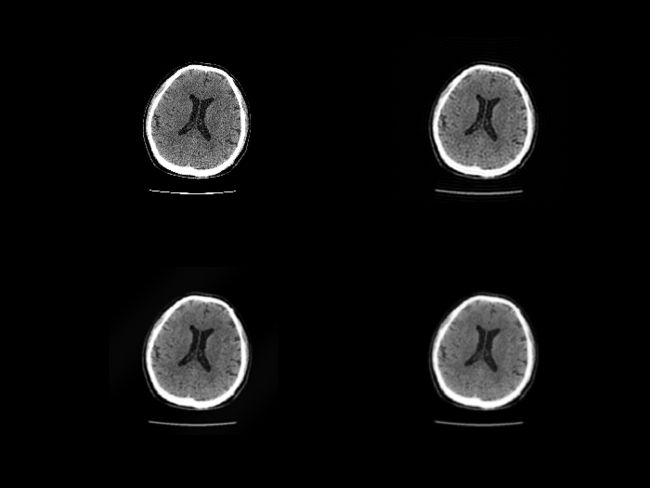
- 对图片nao.jpg 进行低通滤波,比较理想,巴特沃斯,高斯三种滤波器的效果(滤波器要求自己编程,不能调用函数)。部分实验结果如下图:
IA = imread('C:\pictures of QQshiyan\nao.jpg'); % 读取原始数据,这里是 n * 1 的数据
figure
subplot(221),imshow(IA);
title('原图像');
%理想低通
s=fftshift(fft2(IA));
%subplot(232), imshow(log(abs(s)),[]);
%title('图像傅里叶变换取对数所得频谱');
[a,b]=size(s);
a0=round(a/2);
b0=round(b/2);
d=50;
for i=1:a
for j=1:b
distance=sqrt((i-a0)^2+(j-b0)^2);
if distance<=d
h=1;
else
h=0;
end
s(i,j)=h*s(i,j);
end
end
s=uint8(real(ifft2(ifftshift(s))));
subplot(222),imshow(s);
title('理想低通滤波所得图像');
f=double(IA);%数据类型转换
g=fft2(f);%图像傅里叶转换
g=fftshift(g);%傅里叶变换平移
F2=log(abs(g));%对傅里叶变换结果取绝对值,然后取对数
[N1,N2]=size(g);%傅里叶变换图像尺寸
n=2;%参数赋初始值
d0=50;
n1=fix(N1/2);%数据圆整
n2=fix(N2/2);%数据圆整
for i=1:N1%遍历图像像素
for j=1:N2
d=sqrt((i-n1)^2+(j-n2)^2);
if d==0
h=0;
else
h=1/(1+(d/d0)^(2*n));
end
result(i,j)=h*g(i,j);%?图像矩阵计算处理
end
end
F3=log(abs(result));%对傅里叶变换结果取绝对值,然后取对数
result=ifftshift(result);
X2=ifft2(result);
X3=uint8(real(X2));
subplot(223),imshow(uint8(X3))
title('Butterworth低通滤波图像');
[f1,f2]=freqspace(size(IA),'meshgrid');
D=100/size(IA,1);
r=f1.^2+f2.^2;
Hd=ones(size(IA));
for i=1:size(IA,1)
for j=1:size(IA,2)
t=r(i,j)/(D*D);
Hd(i,j)=exp(-t);
end
end
Y=fft2(double(IA));
Y=fftshift(Y);
Ya=Y.*Hd;
Ya=ifftshift(Ya);
Ia=real(ifft2(Ya));
subplot(224),imshow(uint8(Ia));
title('高斯低通滤波处理');
在一幅图像中,其低频成分对应者图像变化缓慢的部分,对应着图像大致的相貌和轮廓。而其高频成分则对应着图像变化剧烈的部分,对应着图像的细节(图像的噪声也属于高频成分)。低频滤波器可以平滑图像,滤去图像的噪声。低通滤波器滤除了高频成分,所以使得图像模糊。由于理想低通滤波器的过度特性过于急峻,所以会产生了振铃现象。巴特沃斯滤波器随着次数的增加,振铃现象会越来越明显。高斯滤波器的过度特性非常平坦,不会产生振铃现象的。
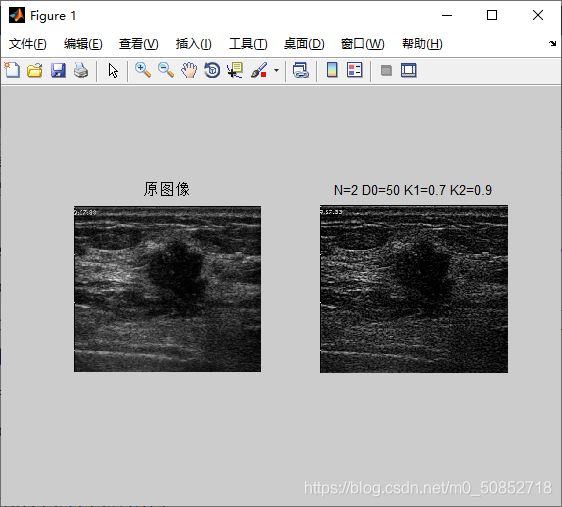
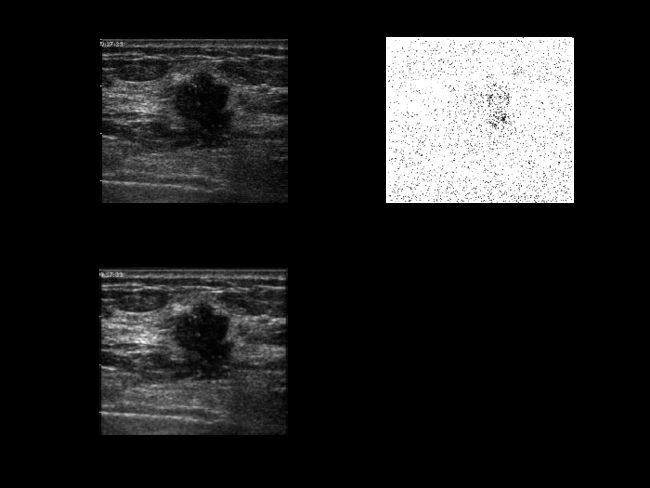
- 对超声图像通过巴特沃斯高通进行高频提升滤波增强,改变滤波参数的值,观察增强效果。
clc
clear
f = imread('C:\pictures of QQshiyan\超声.tif'); %读取彩色图像
n=2;
D0=50;
%%%%%巴特沃斯高通滤波
figure('Name', '图像加入巴特沃斯高通滤波'); %标题
[M, N] = size(f);
a = fft2(f);
a = fftshift(a);
m1 = fix(M / 2); n1 = fix(N / 2);
for u = 1:M
for v = 1:N
D1 = sqrt((u - m1)^2 + (v - n1)^2);
if D1 == 0
H1(u, v) = 0;
else
% H(u,v)=1/(1+0.414*(50/D1)^4);%截至频率为50
H1(u, v) = 1 / (1 + (D0/ D1)^(2*n)); %2阶巴特沃斯高通滤波器,截至频率为50
end
end
end
F1 = H1 .* a;
F1 = ifftshift(F1);
I2 = abs(ifft2(F1));
subplot(2, 2, 1);
imshow(f)
title('原始图像')
subplot(2, 2, 2);
imshow(I2)
title('巴特沃斯高通滤波后的图像')
%高频强调滤波
FF = 0.7 + 0.9 * (1 - H1);
G1 = FF .* a;
result3 = ifftshift(G1);
J8 = ifft2(result3);
J9 = uint8(real(J8));
subplot(2, 2, 3)
imshow(J9)
title('高频强调滤波后的图像')
高频强调滤波方法传递函数:Hhfe(u,v) = k1
+k2Hhp(u,v);加入一个偏移量同时乘以一个大于1的常数,使用原图像中的一部分低频分量进入高频区域,而在高频滤波后被保留下来,从而不仅保持一些光滑区域灰度,又使边缘得到增强,而且整幅图像的层次也较丰富,不那么昏暗了。高频强调滤波方法是保留了高频分量的同时,加入了背景的低频分量。
本实验中,通过定义巴特沃斯高通滤波器H1(u, v) = 1 / (1 + (D0/
D1)^(2*n));使n=2,D0=50;用巴特沃斯高通滤波器和原图像频域相乘可实现高通,保留图像高频分量,再通过定义k1=0.7,k2=0.9使原图像中的一部分低频分量进入高频区域。
高频滤波起到了锐化效果,且k2/k1值越大,表面高频分量比低频分量的比值越高,图像锐化效果越好
。