冬至·特辑：Note4---二叉树的链式结构

---

目录

前言

1. 二叉树链式结构的实现

1.1 要实现的目标

2.二叉树的创建

2.1代码实现

2.1.1 TreeNode.h

2.1.2 TreeNode.c

3.实现二叉树的遍历

3.1 思路分析

3.2 前/中/后序遍历

3.2.1 TreeNode.h

3.2.2 TreeNode.c

3.2.3 test.c

3.3 递归流程图

4.获取二叉树的节点、叶子节点个数

4.1 思路分析

4.2 代码实现

4.2.1 TreeNode.h

4.2.2 TreeNode.c

4.2.3 test.c

4.3 递归流程图

5.获取二叉树的高度

5.1 思路分析

5.2 代码实现

5.2.1 TreeNode.h

5.2.2 TreeNode.c

5.2.3 test.c

5.3 递归流程图

6.求二叉树的第k层的节点个数

6.1 思路分析

6.2 代码实现

6.2.1 TreeNode.h

6.2.2 TreeNode.c

6.2.3 test.c

6.3 递归流程图

7.查找二叉树中值为x的节点

7.1 思路分析

7.2 代码实现

7.2.1 TreeNode.h

7.2.2 TreeNode.c

7.2.3 test.c

7.3 递归流程图

8.实现二叉树的层序遍历

8.1 思路分析

8.2 代码实现

8.2.1 TreeNode.h

8.2.2 TreeNode.c

8.2.3 Queue.h

8.2.4 Queue.c

8.2.5 test.c

8.3 代码中存在的困惑点

9.判断是否是完全二叉树

9.1 思路分析

9.2 代码实现

9.2.1 TreeNode.h

9.2.2 TreeNode.c

9.2.3 tets.c

10.实现二叉树的销毁

10.1 思路分析

10.2 代码实现

10.2.1 TreeNode.h

10.2.2 TreeNode.c

10.2.3 test.c

后语

---

前言

上篇博客，我们学习了二叉树和堆的概念和结构，以及如何实现堆，和堆的应用。有需要的小伙伴可以点击下方链接：

Note3---初阶二叉树～～-CSDN博客文章浏览阅读770次，点赞43次，收藏27次。这篇博客，我们一起来了解并学习数据结构中的初阶的二叉树的概念和性质；以及堆和堆堆应用二叉树的知识点和内容比较多，友友们一定要有耐心看完（跳到自己需要的部分也是OK的）。https://blog.csdn.net/2301_79184587/article/details/135033457本篇博客，小江带领大家一起学习如何实现二叉树的链式结构+二叉树的性质总结+涉及上篇博客和这篇博客的知识点一些选择题来巩固基础

下面我们就开始今天的学习吧！

---

1. 二叉树链式结构的实现

1.1 要实现的目标

1.实现二叉树的创建（手动创建）

2.实现二叉树的前序、中序、后序遍历

3.获取二叉树的节点、叶子节点个数

4.获取二叉树的高度

5.获取二叉树的第k层的节点个数

6.查找二叉树中值为x的节点

7.实现二叉树的层序遍历

8.判断是否是完全二叉树

9.实现二叉树的销毁

2.二叉树的创建

​​​​​​​

在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入，为了降低大家学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，我们反过头再来研究二叉树真正的创建方式。

2.1代码实现

这是我们要实现的二叉树的图（也可以自定义）：

从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的。

---

2.1.1 TreeNode.h

#pragma once
#include
#include
#include
#include
#include

typedef int DataType;
typedef struct TreeNode
{
	//值 左子树 右子树
	DataType data;
	struct TreeNode* left;
	struct TreeNode* right;
}TNode;

//手动创建一个简单的二叉树
TNode* CreatTree();

---

2.1.2 TreeNode.c

#include"TreeNode.h"
//手动创建一个简单的二叉树
TNode* BuyNode(DataType x)
{
	TNode* node = (TNode*)malloc(sizeof(TNode));
	if (node == NULL)
	{
		perror("malloc error!\n");
		exit(0);
	}
	node->data = x;
	node->left = node->right = NULL;
	return node;
}
TNode* CreatTree()
{
	TNode* node1 = BuyNode(1);
	TNode* node2 = BuyNode(2);
	TNode* node3 = BuyNode(3);
	TNode* node4 = BuyNode(4);
	TNode* node5 = BuyNode(5);
	TNode* node6 = BuyNode(6);
	TNode* node7 = BuyNode(7);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
	node5->left = node7;

	return node1;
}

---

3.实现二叉树的遍历

所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。

访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历

前序：根节点--->左子树--->右子树

中序：左子树--->根节点--->右子树

后序：左子树--->右子树--->根节点

3.1 思路分析

下面主要分析前序递归遍历，中序与后序图解类似，大家可自己动手绘制。

---

3.2 前/中/后序遍历

3.2.1 TreeNode.h

// 二叉树前序遍历
void PreOrder(TNode* root);
// 二叉树中序遍历
void InOrder(TNode* root);
// 二叉树后序遍历
void PostOrder(TNode* root);

---

3.2.2 TreeNode.c

// 二叉树前序遍历
void PreOrder(TNode* root)
{
	//注意判空
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}
// 二叉树中序遍历
void InOrder(TNode* root)
{
	//注意判空
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}
// 二叉树后序遍历
void PostOrder(TNode* root)
{
	//注意判空
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

---

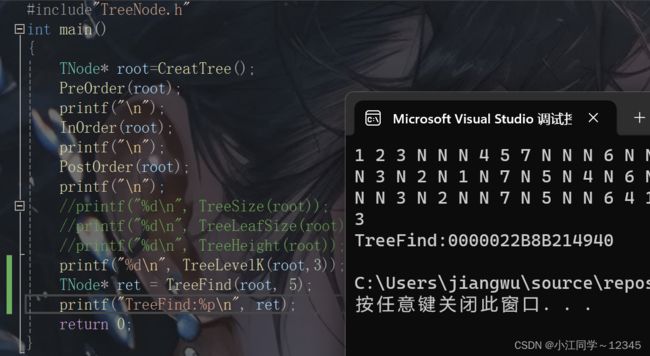
3.2.3 test.c

#include"TreeNode.h"
int main()
{
	TNode* root=CreatTree();
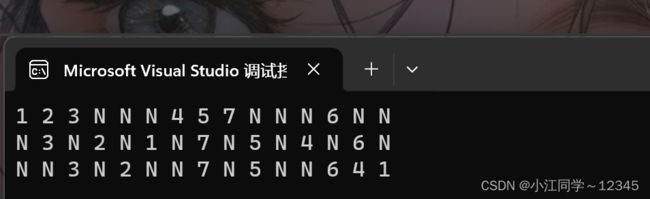
	PreOrder(root);
	printf("\n");
	InOrder(root);
	printf("\n");
	PostOrder(root);
	printf("\n");
	return 0;
}

---

---

3.3 递归流程图

---

4.获取二叉树的节点、叶子节点个数

4.1 思路分析

总思想：递归+分治

1.求节点个数
分治：左子树节点个数+右子树节点个数+1（根节点）

 

2.求叶子节点（无孩子节点）个数

分治：左子树叶子节点个数+右子树叶子节点个数

返回条件：

1. 空 返回0

2. 叶子节点 返回1

 

问题：空树怎么办？ 要判断然后直接返回0

4.2 代码实现

4.2.1 TreeNode.h

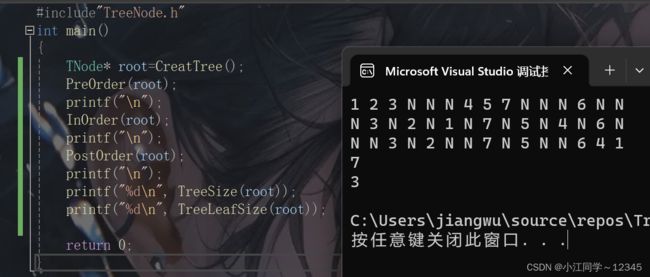
//节点个数
int TreeSize(TNode* root);
//叶子节点个数
int TreeLeafSize(TNode* root);

---

4.2.2 TreeNode.c

//节点个数
int TreeSize(TNode* root)
{
	if (root == NULL)
		return 0;
	return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//叶子节点个数
int TreeLeafSize(TNode* root)
{
	//空树，返回0
	if (root == NULL)
		return 0;
	//叶子节点，返回1
	if (root->left == NULL && root->right == NULL)
		return 1;
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

---

4.2.3 test.c

---

4.3 递归流程图

---

---

5.获取二叉树的高度

5.1 思路分析

递归+分治：

1.空 返回0

2.非空 比较左子树和右子树高度 较大的+1并且返回

5.2 代码实现

---

5.2.1 TreeNode.h

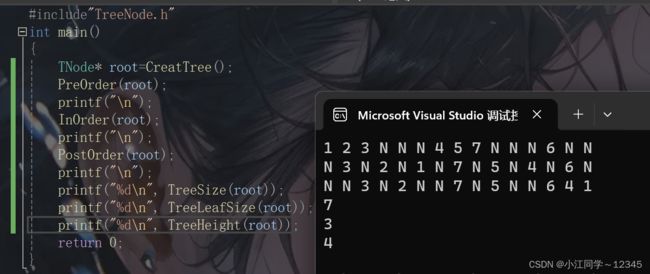
//求高度
int TreeHeight(TNode* root);

---

5.2.2 TreeNode.c

//求高度
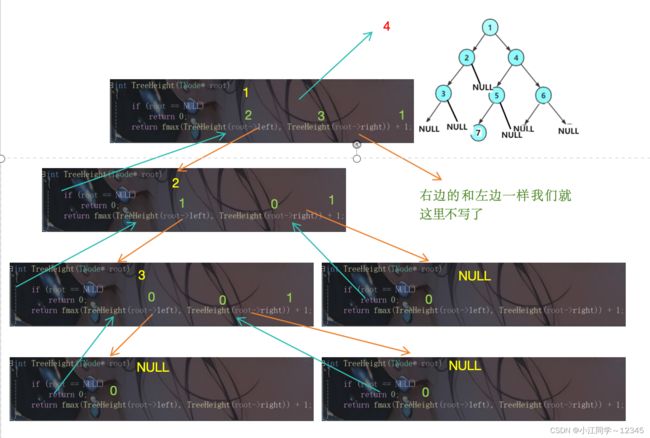
int TreeHeight(TNode* root)
{
	if (root == NULL)
		return 0;
	return fmax(TreeHeight(root->left), TreeHeight(root->right)) + 1;
}

---

5.2.3 test.c

---

5.3 递归流程图

---

6.求二叉树的第k层的节点个数

6.1 思路分析

递归+分治：

1. 为空 返回0

2. 不为空并且k==1（根节点那一层） 返回1

3. 不为空并且k>1 返回左子树（k-1）层总个数+右子树（k-1）总层个数（不包括第一层）

6.2 代码实现

6.2.1 TreeNode.h

//求第k层节点个数
int TreeLevelK(TNode* root, int k);

---

6.2.2 TreeNode.c

//求第k层节点个数
int TreeLevelK(TNode* root, int k)
{
	assert(k > 0);
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return TreeLevelK(root->left, k - 1) + TreeLevelK(root->right, k - 1);
}

---

6.2.3 test.c

---

6.3 递归流程图

---

7.查找二叉树中值为x的节点

7.1 思路分析

递归+分治：

1.空  返回NULL

2.值==x  返回节点

3.值！=x  先左子树遍历，比较+记录   左子树没找到，右子树遍历，比较+遍历

7.2 代码实现

7.2.1 TreeNode.h

//求x的节点
TNode* TreeFind(TNode* root, DataType x);

---

7.2.2 TreeNode.c

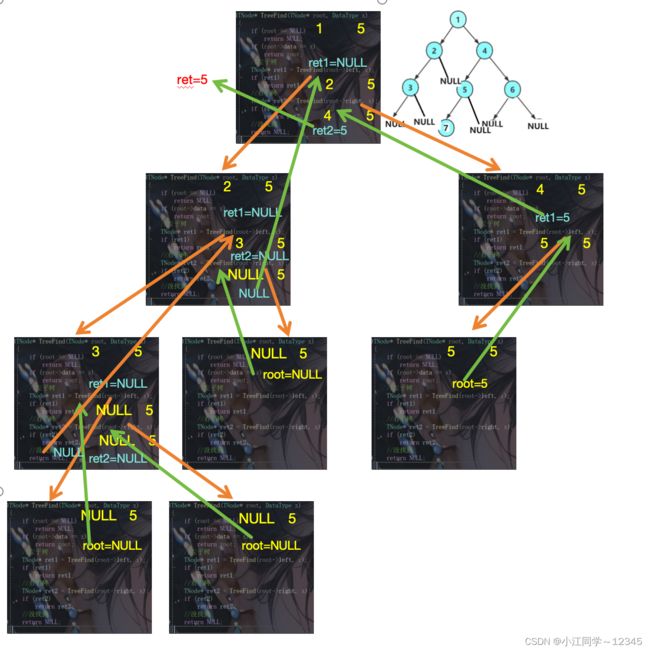
//求x的节点
TNode* TreeFind(TNode* root, DataType x)
{
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;
	//左子树
	TNode* ret1 = TreeFind(root->left, x);
	if (ret1)
		return ret1;
	//右子树
	TNode* ret2 = TreeFind(root->right, x);
	if (ret2)
		return ret2;
	//没找到
	return NULL;
}

---

7.2.3 test.c

---

7.3 递归流程图

---

8.实现二叉树的层序遍历

1.什么是层序遍历？

一层一层遍历二叉树

 

2.层序遍历为什么要单独拿出来讲，而不是和前/中/后序一起讲？

因为层序遍历不需要递归就能实现，但是需要借助队列实现

 

3.为什么要借助队列实现？

因为队列的性质是先进先出，符合二叉树遍历的要求（遍历完一层，就打印一层的内容）

 

4.队列存放节点还是节点的值？
存放节点，因为单独存放值的话，找不到它的左孩子和右孩子

 

5.队列放节点还是节点的指针呢？
节点的指针--->方便查找--->注意修改的Queue.h中QDataType的类型，不再是int类型的值了

---

8.1 思路分析

1. 根节点入队

2.队列不为空的话：

获取头节点--->出队--->打印--->左子树入队--->右子树入队（一层就入队完成了）

继续循环♻️一层一层出

3.队列为空：

循环结束---遍历结束

8.2 代码实现

队列的代码在之前的博客有，这里就不再做解释了，需要的小伙伴点击下方链接：

Note2---栈和队列～～-CSDN博客文章浏览阅读846次，点赞42次，收藏37次。之前，我们学习了顺序表和链表的相关知识，也完成了相应的练习，接下来我们要学习的是栈和队列！本篇将会比较详细的进行讲解栈和队列的相关知识点及如何实现，以及一些）OJ题https://blog.csdn.net/2301_79184587/article/details/134438809

8.2.1 TreeNode.h

//层序遍历
void LevelOrder(TNode* root);

---

8.2.2 TreeNode.c

//层序遍历
void LevelOrder(TNode* root)
{
	Queue q;
	QueueInit(&q);//初始化
	if (root)
		QueuePush(&q, root);
	int LevelSize = 1;
	while (!QueueEmpty(&q))
	{
		//一层一层出
		while (LevelSize--)
		{
			TNode* front = QueueFront(&q);
			QueuePop(&q);
			printf("%d ", front->data);
			//下一层的左子树
			if (front->left)
				QueuePush(&q, front->left);
			//下一层的右子树
			if (front->right)
				QueuePush(&q, front->right);
		}
		printf("\n");
		LevelSize = QueueSize(&q);
	}
	printf("\n");
	QueueDestroy(&q);
}

---

8.2.3 Queue.h

#pragma once
#include"TreeNode.h"
#include
#include
#include
#include
// 链式结构：表示队列 
typedef struct TreeNode* QDataType;
typedef struct QListNode
{
	struct QListNode* _next;
	QDataType _data;
}QNode;

// 队列的结构 
typedef struct Queue
{
	QNode* _head;
	QNode* _tail;
	int size;
}Queue;

// 初始化队列 
void QueueInit(Queue* q);
// 队尾入队列 
void QueuePush(Queue* q, QDataType data);
// 队头出队列 
void QueuePop(Queue* q);
// 获取队列头部元素 
QDataType QueueFront(Queue* q);
// 获取队列队尾元素 
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数 
int QueueSize(Queue* q);
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
int QueueEmpty(Queue* q);
// 销毁队列 
void QueueDestroy(Queue* q);

---

8.2.4 Queue.c

#include"Queue.h"
// 初始化队列 
void QueueInit(Queue* q)
{
	assert(q);
	q->_head = q->_tail = NULL;
	q->size = 0;
}
// 队尾入队列 
void QueuePush(Queue* q, QDataType data)
{
	assert(q);
	QNode* node = (QNode*)malloc(sizeof(QNode));
	if (node == NULL)
	{
		perror("malloc error!\n");
		return;
	}
	node->_data = data;
	node->_next = NULL;
	if (q->_head == NULL)
	{
		q->_head = q->_tail = node;
	}
	else
	{
		q->_tail->_next = node;
		q->_tail = node;
	}
	q->size++;
}
// 队头出队列 
void QueuePop(Queue* q)
{
	assert(q);
	//不为空
	assert(q->_head);
	//只有1给节点，直接free
	if (q->_head->_next == NULL)
	{
		free(q->_head);
		q->_head = NULL;
	}
	else
	{
		QNode* del = q->_head;
		q->_head = q->_head->_next;
		free(del);
		del = NULL;
	}
	q->size--;
}
// 获取队列头部元素 
QDataType QueueFront(Queue* q)
{
	assert(q);
	assert(q->_head);
	return q->_head->_data;
}
// 获取队列队尾元素 
QDataType QueueBack(Queue* q)
{
	assert(q);
	assert(q->_tail);
	return q->_tail->_data;
}
// 获取队列中有效元素个数 
int QueueSize(Queue* q)
{
	assert(q);
	return q->size;
}
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
int QueueEmpty(Queue* q)
{
	assert(q);
	if (q->_head == NULL)
		return 1;
	return 0;
}
// 销毁队列 
void QueueDestroy(Queue* q)
{
	assert(q);
	QNode* del = q->_head;
	while (del)
	{
		QNode* next = del->_next;
		free(del);
		del = NULL;
		del = next;
	}
	q->_head = q->_tail = NULL;
	q->size = 0;
}

---

8.2.5 test.c

---

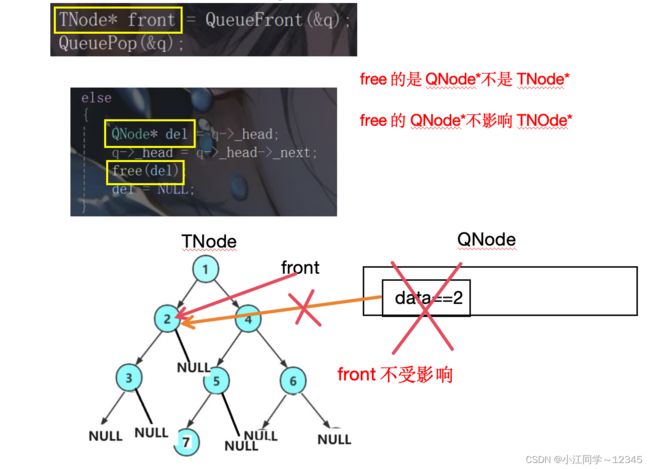
8.3 代码中存在的困惑点

1. front不是free了吗，还能使用吗？为什么？

2.为什么队列中的有效个数（k）就代表是第k层？

因为获取到该层的头节点时，头节点的下一层左右子树不为空的节点会存储到队列里面，当该层的节点都出队之后，下一层的全部节点也已经入队

此时队里面只有下一层的节点个数，要知道LevelSize代表的是内循环次数，此时队里面有K个节点，出队K次刚刚好

9.判断是否是完全二叉树

9.1 思路分析

关键点---只要不连续就不是完全二叉树---依据层序遍历的基础上实现

怎么判断是否连续？

层序遍历遍历到空结束，判断后面是否为空，为空则为完全二叉树；非空则不是完全二叉树

​​​​​​​注意⚠️

不存在空已经进去了的情况，但是后面的非空还没进去的情况（可以自己尝试举例看看）

9.2 代码实现

9.2.1 TreeNode.h

//判断是否是完全二叉树
bool TreeComplete(TNode* root);

---

9.2.2 TreeNode.c

//判断是否是完全二叉树
bool TreeComplete(TNode* root)
{
	Queue q;
	QueueInit(&q);//初始化
	if (root)
		QueuePush(&q, root);
	int LevelSize = 1;
	while (!QueueEmpty(&q))
	{
			TNode* front = QueueFront(&q);
			QueuePop(&q);
			//判空
			if (front == NULL)
				break;

			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
	}
	//遇到空之后，判别后面是否为空
	while (!QueueEmpty(&q))
	{
		TNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}

---

9.2.3 tets.c

 

---

10.实现二叉树的销毁

10.1 思路分析

1. 用什么顺序遍历二叉树？

后序遍历

因为后序遍历，不用考虑左右子树的保存，更加方便

当然，前/中序也可以写

 

前序首先会free根节点，这就需要保存左右子树，否则找不到左右子树

中序会在free完左子树之后，free根节点，这就需要保存右子树，否则找不到右子树

后序最后才free根节点

2. 用一级指针还是二级指针？

一级指针，前面我们说过最好保证指针级数一致，但是一级指针需要手动置空

10.2 代码实现

10.2.1 TreeNode.h

//销毁
void DestroyTree(TNode* root);

---

10.2.2 TreeNode.c

//销毁
void DestroyTree(TNode* root)
{
	if (root == NULL)
		return;
	//后序
	DestroyTree(root->left);
	DestroyTree(root->right);
	free(root);
}

---

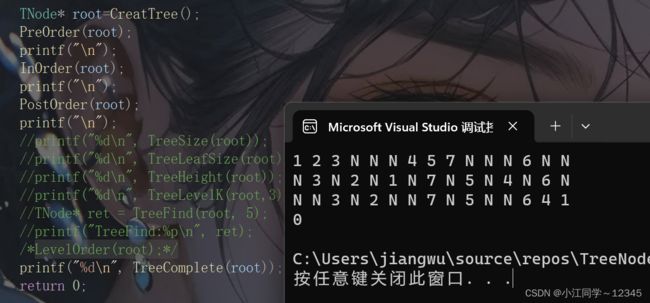
10.2.3 test.c

#include"TreeNode.h"
#include"Queue.h"
int main()
{
	TNode* root=CreatTree();
	PreOrder(root);
	printf("\n");
	InOrder(root);
	printf("\n");
	PostOrder(root);
	printf("\n");
	//printf("%d\n", TreeSize(root));
	//printf("%d\n", TreeLeafSize(root));
	//printf("%d\n", TreeHeight(root));
	//printf("%d\n", TreeLevelK(root,3));
	//TNode* ret = TreeFind(root, 5);
	//printf("TreeFind:%p\n", ret);
	/*LevelOrder(root);*/
	printf("%d\n", TreeComplete(root));
	DestroyTree(root);
	root = NULL;
	return 0;
}

---

后语

本次的博客，我们介绍了如何实现二叉树的链式结构。下篇博客，我们将一起练习二叉树的知识运用，包含性质题，选择题，oj题。

---

本次的分享到这里就结束了！！！

PS：小江目前只是个新手小白。欢迎大家在评论区讨论哦！有问题也可以讨论的！

如果对你有帮助的话，记得点赞+收藏⭐️+关注➕