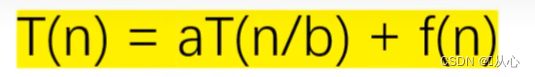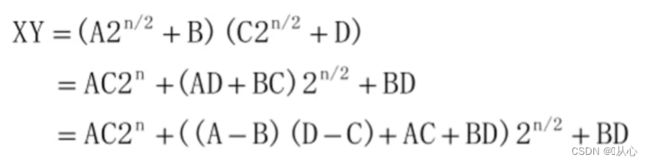高级算法设计与分析(二) -- 递归与分治策略
系列文章目录
高级算法设计与分析(一) -- 算法引论
高级算法设计与分析(二) -- 递归与分治策略
高级算法设计与分析(三) -- 动态规划
高级算法设计与分析(四) -- 贪心算法
高级算法设计与分析(五) -- 回溯法
高级算法设计与分析(六) -- 分支限界法
高级算法设计与分析(七) -- 概率算法和NP完全性理论
高级算法设计与分析(八) -- 总结
目录
系列文章目录
前言
一、递归的概念
1.1、eg:累加函数
1.2、eg:斐波那契数列
1.3、eg:阿克曼函数
1.4、eg:汉诺塔问题
二、分治法的基本思想
三、二分搜索技术
四、大整数的乘法
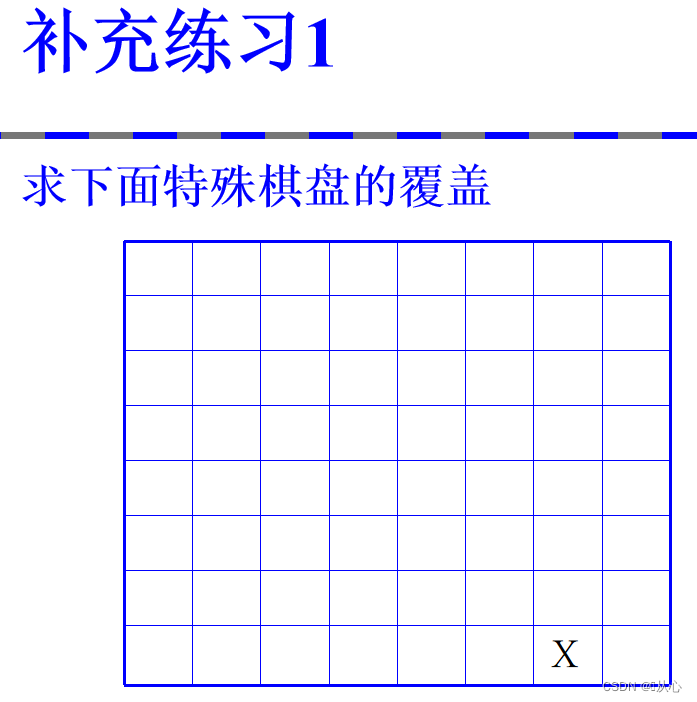
五、棋盘覆盖
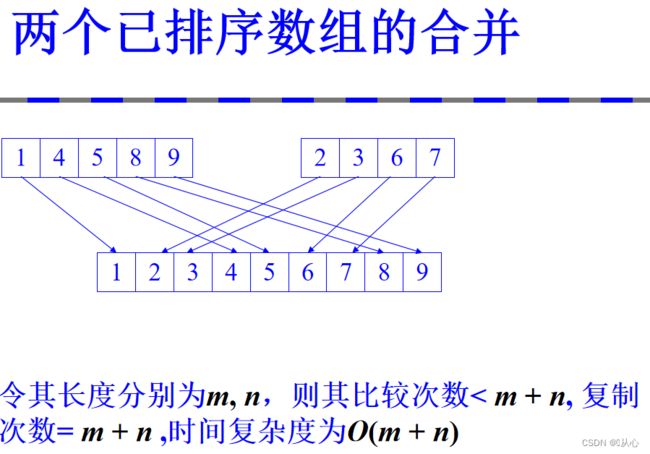
六、合并排序
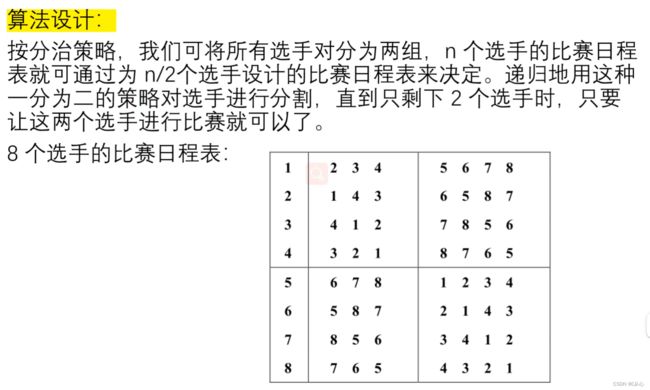
七、循环赛日程表
递归算法小结
八、***最大子段和
九、矩阵乘法
十、线性时间选择
习题
汉诺塔问题
二分搜索法
大整数的乘法
棋盘覆盖
编辑
合并排序
循环赛日程表
前言
tips:这里只是总结,不是教程哈。鉴于本人写字如画符,就不出视频教程了,如实在有需要,请在文章下方留言。当然,文章有任何问题,也请留言,谢谢!
这个系列用另一种形式,把习题放在最下面,看看好用不。
本系列文章最后一文会进行简要全部总结,以及思维导图放在最后一篇文章最下面,请自行获取。
一、递归的概念
直接或间接地调用自身的算法称为递归算法。
1.1、eg:累加函数
时间:O(n);空间:O(n)
改成非递归。
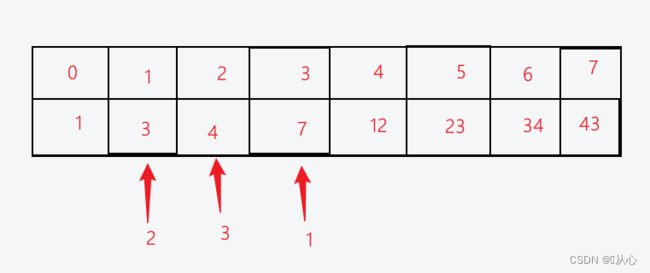
1.2、eg:斐波那契数列
斐波那契数列直观理解:第1,2个数为1,之后每个数为前两个数之和
eg:1,1,2,3,5,8,13……
1.3、eg:阿克曼函数
阿克曼比较难理解:
直接给例子:
A(0,0)=1
A(0,1)=2
A(1,0)=A(0,1)=2
A(1,1)=A(0,A(1,0))=A(0,2)=3
……
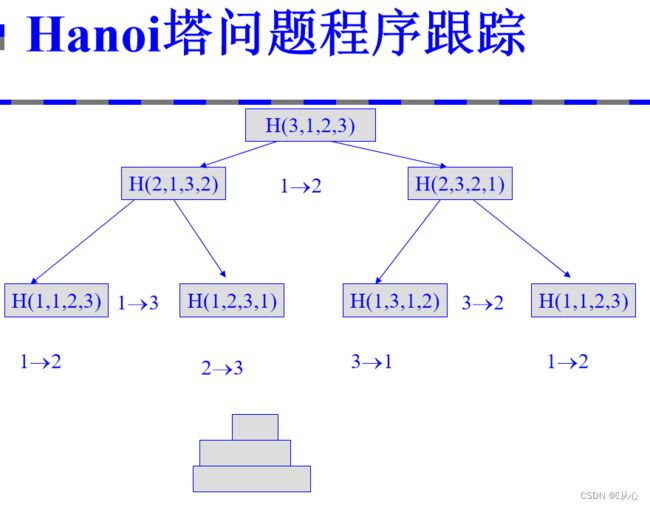
1.4、eg:汉诺塔问题
问题描述:把圆盘从大到小摆到另一个柱子
要求:在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
二、分治法的基本思想
![]()
一个规模为n的问题,分为规模均为n/b的a个子问题,f(n)表示其他部分的时间复杂性
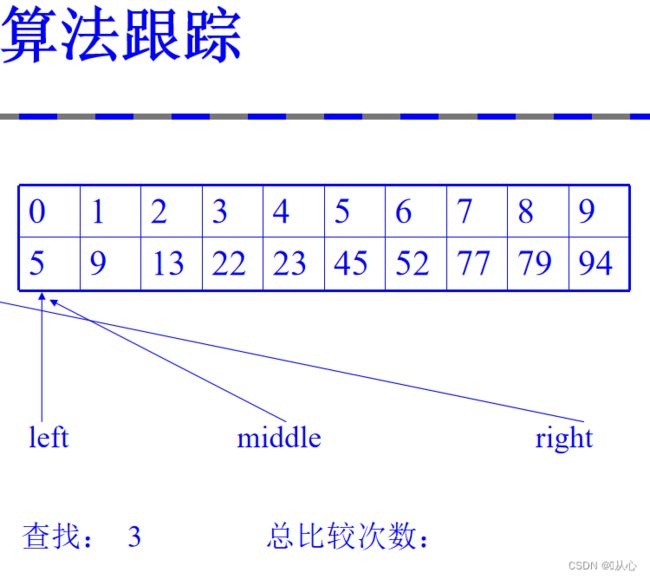
三、二分搜索技术
原理简单理解:如下,想要找4的所在,先找数组下标中间位置,即(7+0)/2=3.5~3,可以先找到7,比较与目标大小,这里目标更小,在前一部分找,即数组下标0-2中,(2+0)/2=1,可以找到3,同理最后找到4.
四、大整数的乘法
1、一般情况下的乘法
计算机运行加法的运算,比运行乘法的运算快得多,所以时间复杂度一般只考虑乘法运算。
2、改进后的乘法
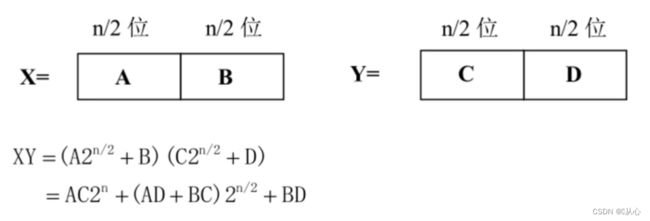
理解:XY为两个n位乘数,把X前n/2位记为A,后n/2位记为B,把Y前n/2位记为C,后n/2位记为D,(下式是对二进制乘数计算,对十进制乘数计算一个将2^(n/2)变为10^(n/2))
3、一般情况下的计算式
五、棋盘覆盖
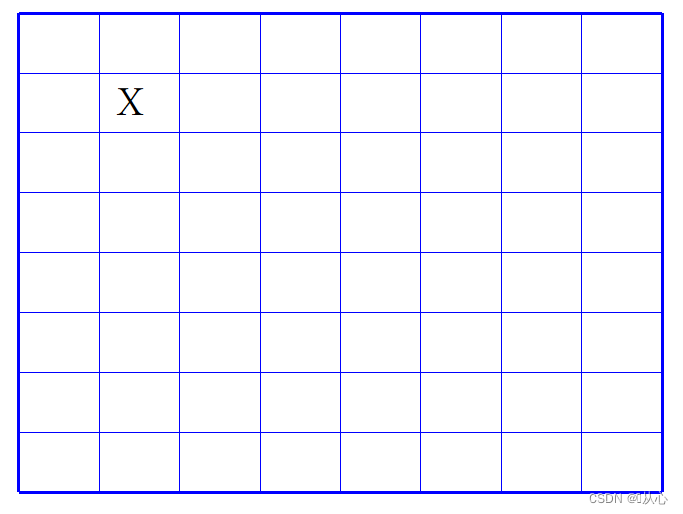
1、问题描述:
在一个2^k*2^k棋盘中,有一个方格与其他不同(如下X处),用4中不同的L形骨牌(即朝向不同的占3个方格的骨牌,看图更好理解)去覆盖棋盘,要求骨牌全部占满棋盘,不多余,不留空,不重叠。
2、基本思想:
1、将2^k*2^k棋盘分割为4个2^(k-1)*2^(k-1)棋盘
2、特殊方格在其中一个区域中,将其他三个无特殊方格的区域用一个L形骨牌覆盖在汇合处。
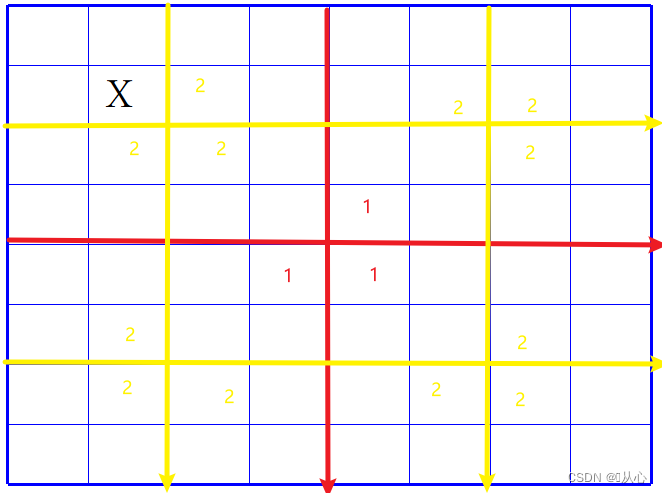
ge:第一步将棋盘分割(红线),
第二步:X在左上方区域,即用一个L形骨牌覆盖其他三个无X区域(3个红色的1处为一个骨牌),使得其他三个区域也分别成为一个有特殊方格的区域,
开始递归:将右上方部分也分为4个棋盘,其中X在一个区域,其他区域用一个L形骨牌共同覆盖,
以此类推……
六、合并排序
七、循环赛日程表
1、问题描述:
设有n=2^k个运动员要进行循环赛。现要设计一个满足以下要求的比赛日程表:
(1)每个选手必须与其他n-1个选手各赛一次;
(2)每个选手一天只能参赛一次;
(3)循环赛在n-1天内结束
递归算法小结
八、***最大子段和
问题描述:
给定n个整数(可能为负整数)组成的序列(a,b,c,d,……), 寻找它的某个连续子段,使得其和最大。例如(1,12,-7,34,-3,-23,4,)最大子段是{1,12,-7,34 }其和为40。
1、穷举法
毫无技术含量!!!
2、分治法
分成两部分,3种情况
1、最大子段和在左边
2、最大子段和在右边
3、最大子段和跨过两个部分(从中间位置分别向左右两边求一个最大的数,然后相加)
九、矩阵乘法
合并的时间复杂度为n^2
改进:
算法分析:
十、线性时间选择
习题
汉诺塔问题
二分搜索法
10个:1,2,4,8,16,32,64,128,256,512
天平可以放两端7个:1,3,9,27,81,243,729;如秤2克的东西,可以1+2=3