MATLAB机器人工具箱 机械臂仿真
MATLAB机器人工具箱 机械臂仿真
-
学习自B站:Nino_FM
-
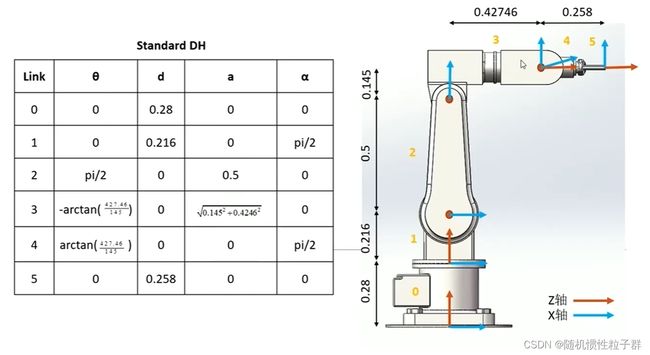
采用 Standard DH 建模法
旋转算子
R = rotx(pi/2)
R =
1.0000 0 0 0 0.9996 -0.0274 0 0.0274 0.9996 % 显然结果有问题
rotx(pi/2/pi*180)
ans =
1 0 0 0 0 -1 0 1 0
rotx(90)
ans =
1 0 0 0 0 -1 0 1 0
机械臂建模
Standard DH
clc;clear
% Standard DH
L(1) = Link('revolute','d',0.216,'a',0,'alpha',pi/2);
L(2) = Link('revolute','d',0,'a',0.5,'alpha',0,'offset',pi/2);
L(3) = Link('revolute','d',0,'a',sqrt(0.145^2+0.42746^2),'alpha',0,'offset',-atan(427.46/145));
L(4) = Link('revolute','d',0,'a',0,'alpha',pi/2,'offset',atan(427.46/145));
L(5) = Link('revolute','d',0.258,'a',0,'alpha',0);
Five_dof = SerialLink(L,'name','5-dof');
Five_dof.base = transl(0,0,0.28);
Five_dof.teach
代码显示
机器人工具箱 常用函数
rotx() roty() rotz() eul2r() tr2eul() rpy2r() tr2rpy()
欧拉角
例子: r1 = eul2r(90,60,30) 与 r2 = rotz(90) * roty(60) * rotz(30) 等价
r1 =
-0.5000 -0.8660 0 0.4330 -0.2500 0.8660 -0.7500 0.4330 0.5000
r2 =
-0.5000 -0.8660 0 0.4330 -0.2500 0.8660 -0.7500 0.4330 0.5000
例子: r3 = rpy2r(90,60,30) 与 r4 = rotz(30)roty(60)rotx(90) 等价
r3 =
0.4330 0.7500 0.5000 0.2500 0.4330 -0.8660 -0.8660 0.5000 0
r4 =
0.4330 0.7500 0.5000 0.2500 0.4330 -0.8660 -0.8660 0.5000 0
旋转<------------------>变换矩阵
trotx() troty() trotz() eul2tr() tr2eul() rpy2tr() tr2rpy()
例子: T1 = eul2tr(90,60,30) 与 T2 = trotz(90) * troty(60) * trotz(30) 等价
T1 =
-0.5000 -0.8660 0 0 0.4330 -0.2500 0.8660 0 -0.7500 0.4330 0.5000 0 0 0 0 1.0000
T2 =
-0.5000 -0.8660 0 0 0.4330 -0.2500 0.8660 0 -0.7500 0.4330 0.5000 0 0 0 0 1.0000
例子: T3 = rpy2tr(90,60,30) 与 T4 = trotz(30) * troty(60) * trotx(90) 等价
T3 =
0.4330 0.7500 0.5000 0 0.2500 0.4330 -0.8660 0 -0.8660 0.5000 0 0 0 0 0 1.0000
T4 =
0.4330 0.7500 0.5000 0 0.2500 0.4330 -0.8660 0 -0.8660 0.5000 0 0 0 0 0 1.0000
位移、旋转矩阵<------------------>变换矩阵
transl() t2r() r2t()
例子: T = transl(1.5,1,0.5) * trotx(30) * trotz(60)
P = transl(T)
R = t2r(T)
T =
0.5000 -0.8660 0 1.5000 0.7500 0.4330 -0.5000 1.0000 0.4330 0.2500 0.8660 0.5000 0 0 0 1.0000
P =
1.5000 1.0000 0.5000
R =
0.5000 -0.8660 0 0.7500 0.4330 -0.5000 0.4330 0.2500 0.8660
帮助文档
doc SerialLink
-
创建一个SerialLink机器人对象
SerialLink.teach
-
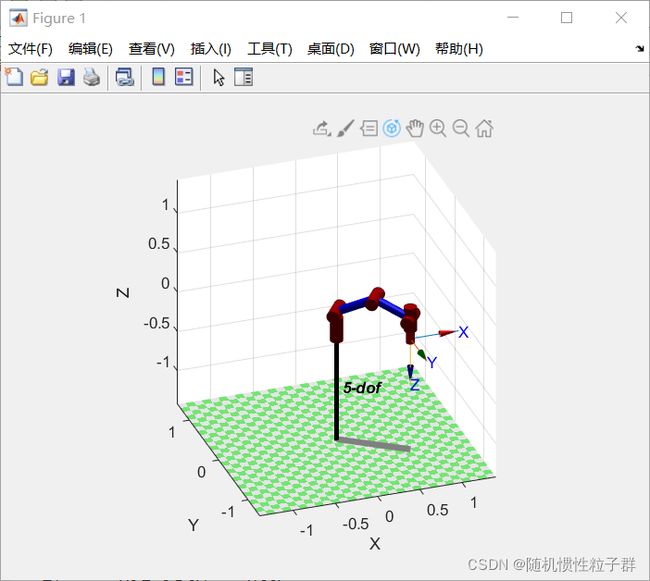
模型展示(SerialLink.plot)
q = [0 0 0 0 0]; % 初始位姿 Five_dof = SerialLink(L,'name','5-dof'); Five_dof.plot(q)
-
三维模型展示(plot3d)
mdl_puma560; p560.plot3d(qz,'view',[0 0]);
-
正向运动学(fkine)
q0 = [pi/2 pi/2 0 0 0]; T = Five_dof.fkine(q0)
T =
0 1 0 0
-1 0 0 -0.645
0 0 1 0.9015
0 0 0 1
-
逆向运动学(ikine、ikunc......)
q1 = Five_dof.ikine(T,'mask',[1 1 1 1 1 0]) q2 = Five_dof.ikunc(T)
q1 =
1.5708 1.5708 -0.0000 0.0000 0
q2 =
1.5708 1.5708 0.0000 0.0000 -0.0000
工作空间可视化
关节空间随机生成变量------(fkine)------>变换矩阵------(transl)------>三维坐标
-
rand函数
在[m,n]内随机生成一个数字:m + rand * (m-n)
-
随机关节空间变量:q= q_min + rand * (q_max - q_min)
L(1).qlim = [-150,150]/180*pi; L(2).qlim = [-100,90]/180*pi; L(3).qlim = [-90,90]/180*pi; L(4).qlim = [-100,100]/180*pi; L(5).qlim = [-180,180]/180*pi; num = 30000; % 迭代次数 P = zeros(num, 3); % 初始化P for i =1:num q1 =L(1) .qlim(1) + rand * (L(1).qlim(2) - L(1).qlim(1)); q2 =L(2) .qlim(1) + rand * (L(2).qlim(2) - L(2).qlim(1)); q3 =L(3) .qlim(1) + rand * (L(3).qlim(2) - L(3).qlim(1)); q4 =L(4) .qlim(1) + rand * (L(4).qlim(2) - L(4).qlim(1)); q5 =L(5) .qlim(1) + rand * (L(5).qlim(2) - L(5).qlim(1)); q = [q1 q2 q3 q4 q5]; T = Five_dof.fkine(q); P(i, :) = transl(T); end plot3(P(:,1),P(:,2),P(:,3),'b.','markersize',1); hold on grid on daspect([1 1 1]); view([45 45]); Five_dof.plot([0 0 0 0 0]);
可视化显示
轨迹规划
-
五次多项式轨迹(tpoly)
t = linspace(0,2,51); [P,dP,ddP] = tpoly(0,3,t); % 指定初末速度 %[P,dP,ddP] = tpoly(0,3,51,0.02,0.01);
-
混合曲线轨迹(lspb)
t = linspace(0,2,51); [P,dP,ddP] = lspb(0,3,t); % 指定最大速度 %[P,dP,ddP] = tpoly(0,3,51,0.1);
-
多维轨迹(mtraj)
% 例子: (0,0)--------->(3,4) t = linspace(0,2,51); [P,dP,ddP] = mtraj(@tpoly,[0 0],[3 4],t);
-
多维多段轨迹(mstraj)
% 例子: (0,0)----(2s)---->(3,4)----(1s)---->(1,2) % TRAJ = mstraj(WP,QDMAX,TSEG,Q0,DT,TACC,OPTIONS) WP = [0,0;3,4;1,2]; P1 = mstraj(wp,[],[2,1],[],0.04,0); P2 = mstraj(wp,[],[2,1],[],0.04,0.5);
-
实例演示
给定位置(0.7,-0.5,0)--------------------->(0.7,0.5,0.5)
T1 = transl(0.7,-0.5,0)*trotx(180); T2 = transl(0.7,0.5,0)*trotx(180); q1 = Five_dof.ikunc(T1); q2 = Five_dof.ikunc(T2); Five_dof.plot(q1); pause; Five_dof.plot(q2);
P1/P2 -----------(mtraj)----------->Traj-----------(transl)----------->T-----------(ikunc)----------->Qtraj
轨迹:'trail' , 'b'
保存动画:'movie' , 'trail.gif'
P1 = [0.7,-0.5,0]; P2 = [0.7,0.5,0.5]; t = linspace(0,2,51); Traj = mtraj(@tpoly,P1,P2,t); n = size(Traj,1); T = zeros(4,4,n); for i = 1:n T(:, :, i) = transl(Traj(i,:))*trotx(180); end Qtraj = Five_dof.ikunc(T); Five_dof.plot(Qtraj); % 绘制末端轨迹 %Five_dof.plot(Qtraj,'trail','b') % 自动保存动画 %Five_dof.plot(Qtraj,'movie','trail.gif');
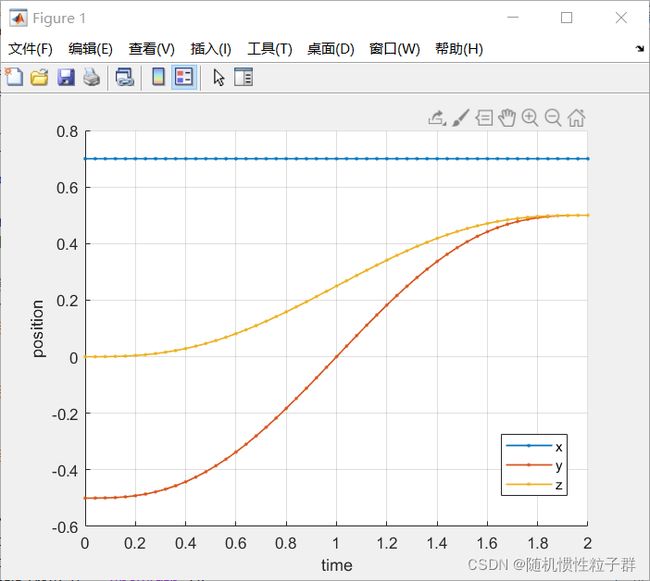
绘制图像
hold on
plot(t,Traj(:,1),'.-','linewidth',1);
plot(t,Traj(:,2),'.-','linewidth',1);
plot(t,Traj(:,3),'.-','linewidth',1);
grid on
legend('x','y','z');
xlabel('time');
ylabel('position');
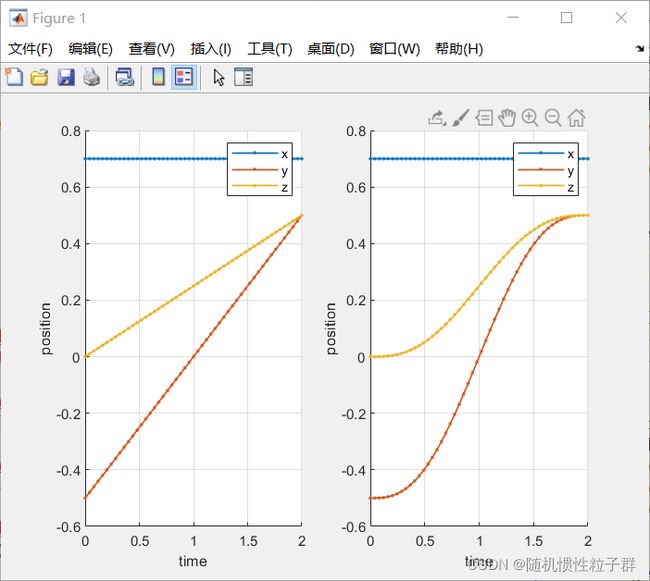
% 线性插值
T_liner = trinterp(T1,T2,51);
P_liner = transl(T_liner);
t1 = linspace(0,2,51);
subplot(1,2,1);
hold on
plot(t1,P_liner(:,1),'.-','linewidth',1);
plot(t1,P_liner(:,2),'.-','linewidth',1);
plot(t1,P_liner(:,3),'.-','linewidth',1);
grid on
legend('x','y','z');
xlabel('time');
ylabel('position');
% 五次多项式插值
T_tpoly = trinterp(T1,T2,tpoly(0,2,50)/2);
P_tpoly = transl(T_tpoly);
t2 = linspace(0,2,50);
subplot(1,2,2);
hold on
plot(t2,P_tpoly(:,1),'.-','linewidth',1);
plot(t2,P_tpoly(:,2),'.-','linewidth',1);
plot(t2,P_tpoly(:,3),'.-','linewidth',1);
grid on
legend('x','y','z');
xlabel('time');
ylabel('position');
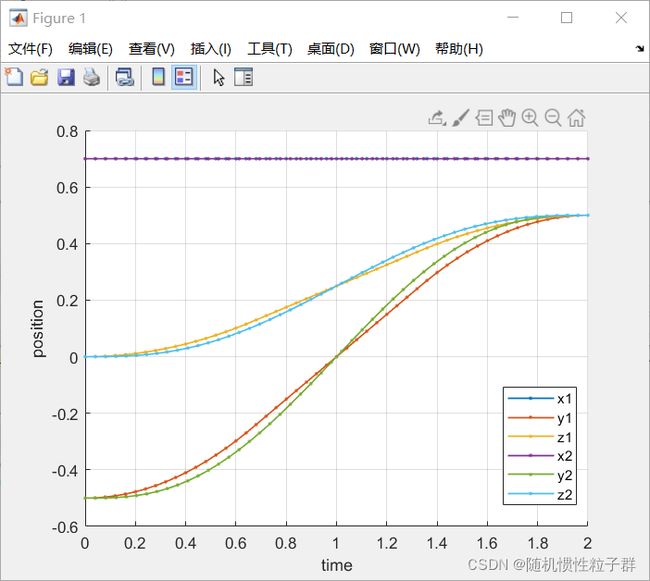
笛卡尔轨迹ctraj
% 笛卡尔轨迹ctraj
T = ctraj(T1,T2,51);
t1 = linspace(0,2,51);
P1 = transl(T);
hold on
plot(t1,P1(:,1),'.-','linewidth',1);
plot(t1,P1(:,2),'.-','linewidth',1);
plot(t1,P1(:,3),'.-','linewidth',1);
T = ctraj(T1,T2,tpoly(0,2,50)/2);
t2 = linspace(0,2,50);
P2 = transl(T);
hold on
plot(t2,P2(:,1),'.-','linewidth',1);
plot(t2,P2(:,2),'.-','linewidth',1);
plot(t2,P2(:,3),'.-','linewidth',1);
grid on
legend('x1','y1','z1','x2','y2','z2');
xlabel('time');
ylabel('position');
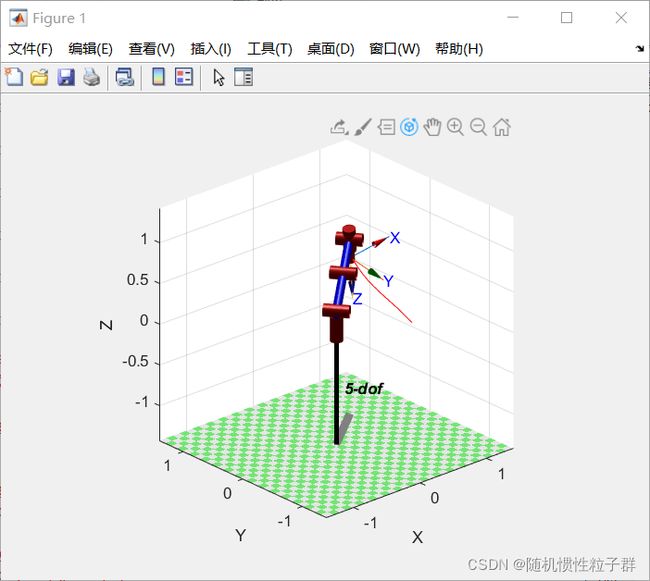
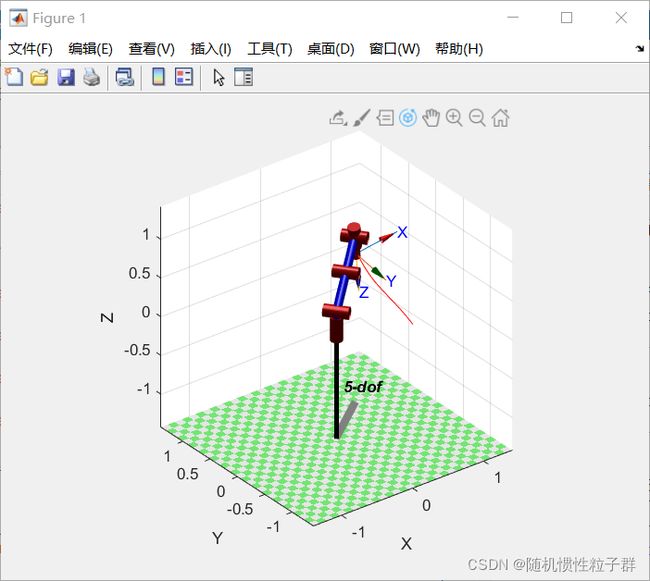
给定位置和姿态
(0.7,-0.5,0)* troty(150)--------------->(0.7,0.5,0.5)* trotx(200)
T1 = transl(0.7,-0.5,0)*troty(150); T2 = transl(0.7,0.5,0.5)*trotx(200); q1 = Five_dof.ikunc(T1); q2 = Five_dof.ikunc(T2); Five_dof.plot(q1); pause Five_dof.plot(q2);
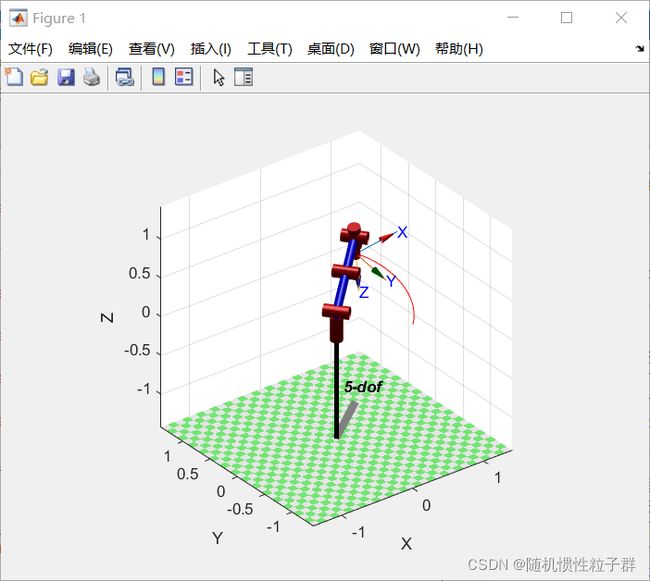
T1、T2------(tr2rpy)----->rpy1、rpy2------(mtraj)----->rpy_traj------(tr2rpy)----->T_raj_rot
rpy1 = [0,150,0]; %绕y轴转150度 rpy2 = [200,0,0]; %绕x轴转200度 t = linspace(0,2,51); rpy_traj = mtraj(@tpoly,rpy1,rpy2,t); T_traj_rot = rpy2tr(rpy_traj); P1 = transl(T1); P2 = transl(T2); P_traj = mtraj(@tpoly,P1',P2',t); T_traj_transl = transl(P_traj); n = length(t); T_traj = zeros(4,4,n); for i = 1:n T_traj(:,:,i) = T_traj_transl(:,:,i)*T_traj_rot(:,:,i); end q_traj = Five_dof.ikunc(T_traj); Five_dof.plot(q_traj,'trail','r')
上面的轨迹效果不太好,可用下面的代码替换
-
线性插值
% 线性插值 t = linspace(0,2,51); T_traj = trinterp(T1,T2,t/2); q = Five_dof.ikunc(T_traj); Five_dof.plot(q,'trail','r')
-
梯形速度图像插值
% 梯形速度图像插值 t = linspace(0,2,51); T_traj = ctraj(T1,T2,t/2); q = Five_dof.ikunc(T_traj); Five_dof.plot(q,'trail','r')
-
jtraj
% jtraj t = linspace(0,2,51); [q,dq,ddq] = jtraj(q1,q2,t); Five_dof.plot(q,'trail','r')
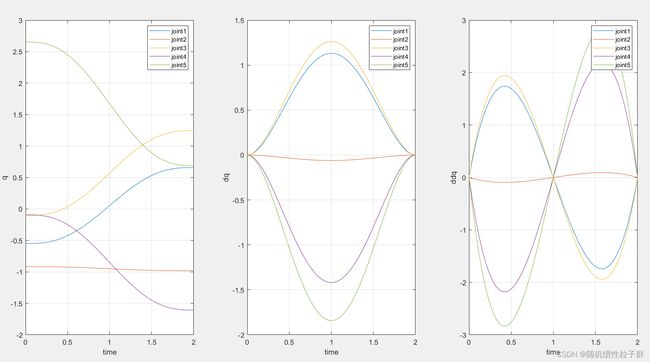
关节变量、速度图像、加速度图像
% 关节变量、速度图像、加速度图像
subplot(1,3,1)
plot(t,q)
grid on
xlabel('time')
ylabel('q')
legend('joint1','joint2','joint3','joint4','joint5')
subplot(1,3,2)
plot(t,dq)
grid on
xlabel('time')
ylabel('dq')
legend('joint1','joint2','joint3','joint4','joint5')
subplot(1,3,3)
plot(t,ddq)
grid on
xlabel('time')
ylabel('ddq')
legend('joint1','joint2','joint3','joint4','joint5')