解决 MATLAB 遗传算法中 exitflg=4 的问题
一、优化问题简介
以求解下述优化问题为例:
P 1 : min p ∑ k = 1 K p k s . t . { ∑ k = 1 K R k r e q l o g ( 1 + α k ∗ p k ) ≤ B b s , ∀ k ∈ K p k ≥ 0 , ∀ k ∈ K \begin{align} {P_1:}&\mathop{\min}_{\bm{p}}{ \sum\limits_{k=1}^K p_k } \nonumber \\ &s.t. \begin{cases} \sum\limits_{k=1}^K \frac{R_k^{req}}{log(1+\alpha_k * p_k) } \leq B^{bs}, \forall k \in \mathcal{K} \nonumber \\ p_k \geq 0, \forall k \in \mathcal{K} \end{cases} \end{align} P1:minpk=1∑Kpks.t.⎩ ⎨ ⎧k=1∑Klog(1+αk∗pk)Rkreq≤Bbs,∀k∈Kpk≥0,∀k∈K
其中, p k p_k pk是决策变量, α k \alpha_k αk、 R k r e q R_k^{req} Rkreq、 B b s B^{bs} Bbs均是已知的正常数, K = { 1 , 2 , … , K } \mathcal{K}=\{1,2,\dots,K\} K={1,2,…,K}表示变量的索引数。
二、有问题的代码
先以 K = 2 K=2 K=2 为例,调用遗传算法,编写下述代码,以求解上述优化问题:
1. 主函数:
clear all
clc
para.K = 2 ;
para.alpha = ones( para.K , 1 );
para.B_bs = 10 ;
para.R_req = [ 3.6702 ; 5.2690 ] ; % 2*rand( para.K , 1 ) + 5 ;
LB = zeros( para.K , 1 ) + 10^(-5);
[X,FVAL,EXITFLAG,OUTPUT] = ga( @(x) myfit(x,para), para.K ,[], [],[],[],LB,[], @(x) nonlcon(x,para),[] )
2. 目标函数:
function f = myfit( x , para )
f = sum(x);
end
3. 非线性约束函数:
function [ g , h ] = nonlcon( x , para )
g = sum( para.R_req ./ log2( 1 + para.alpha .* x' ) ) - para.B_bs;
h=[] ;
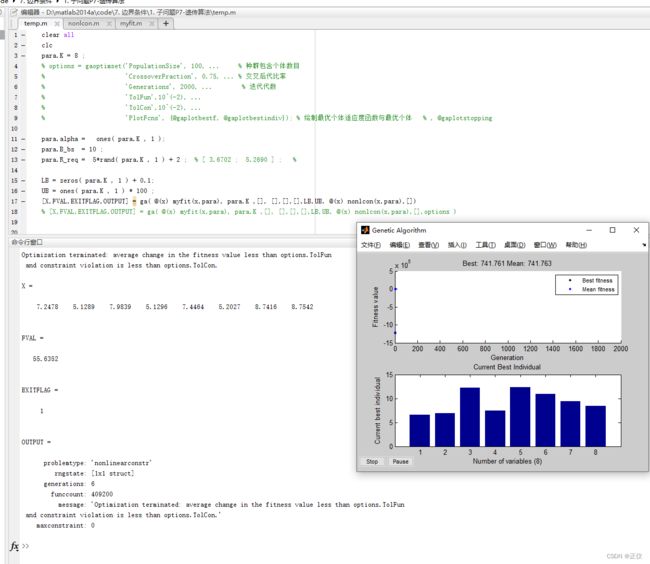
在代码中的参数设定下,我的运行结果不稳定:(MATLAB R2014a版本)
- 运行好的结果如下(exitflg=1):
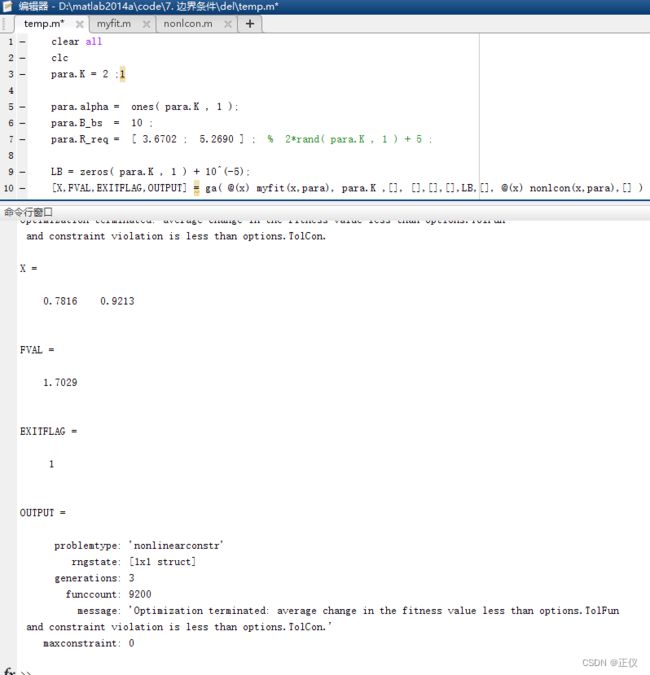
- 运行不好的结果如下(exitflg=4):

GA提示:
Optimization terminated: norm of the step is less than 2.2204e-16
and constraint violation is less than options.TolCon.
GA函数返回迭代终止原因是步长范数过小,显示exitflg=4。
我搜了很多网址,寻找 exitflg=4 的原因,在以下两处资料中得到答案:
(1)官方MATLAB的文档

(2)exitFlag meaning in GA solver
“when the solution change is smaller than matlab capability (exit flag 4), this means you may need to improve your objective function.”
三、解决方案
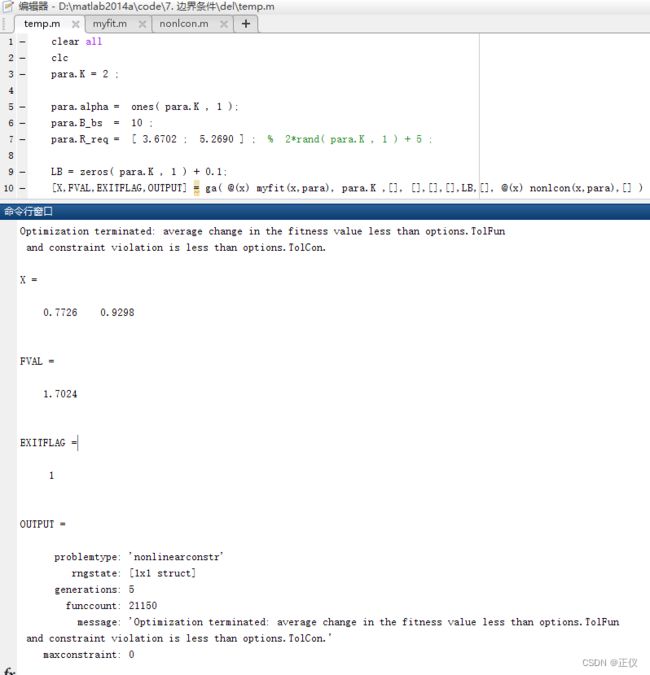
在我的优化问题中,我将 low bound 从原始的 1 0 − 5 10^{-5} 10−5 提高到 0.1 就好了…… (由 log 函数的定义可知,决策变量 p k p_k pk 需要大于等于0,在我的问题中, p k p_k pk越远离0,越不会出现 exitflg=4 的情况,且 p k p_k pk 的最优解也没有取在0的附近,因此我可以设成了0.1)
因此,将main函数改为下式:
clear all
clc
para.K = 2 ;
para.alpha = ones( para.K , 1 );
para.B_bs = 10 ;
para.R_req = [ 3.6702 ; 5.2690 ] ; % 2*rand( para.K , 1 ) + 5 ;
LB = zeros( para.K , 1 ) + 0.1;
[X,FVAL,EXITFLAG,OUTPUT] = ga( @(x) myfit(x,para), para.K ,[], [],[],[],LB,[], @(x) nonlcon(x,para),[] )
此后运行结果非常稳定!
四、其他方案
在摸索 exitflg=4 的原因过程中,除了前述上调 low bound 令其远离 log 小于0的区域以外,我还发现了一些其他两个可有效缓解 exitflg=4 的方案:
- 增大种群规模(如:PopulationSize=300)
- 扩大目标函数(如:给目标函数乘以100倍)
- 增大迭代轮数(如:Generations=2000)
具体调试过程见下图:
(1)目标函数扩大100倍以后:‘Generations’, 为2000、种群规模增长到300 时,exitflg仍为4,但此时已经很接近最优解了。
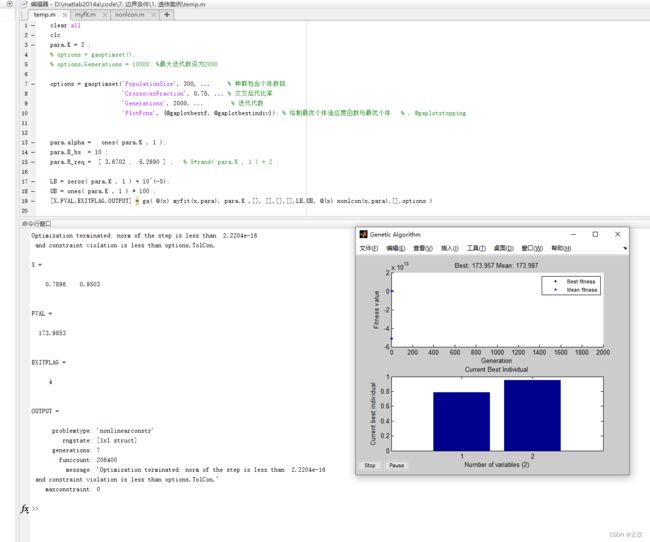
(2)目标函数扩大100倍以后:‘Generations’, 为10000、种群规模增长到300 时(即增大迭代次数),exitflg偶尔为4,大部分时间为1,此时就是最优解
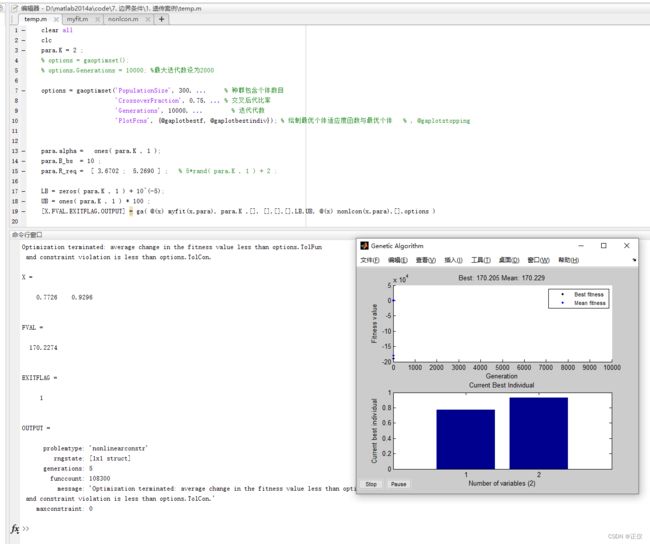
(3)目标函数扩大10000倍以后:‘Generations’, 即使为2000、种群规模为300 时,exitflg大部分情况也会为1
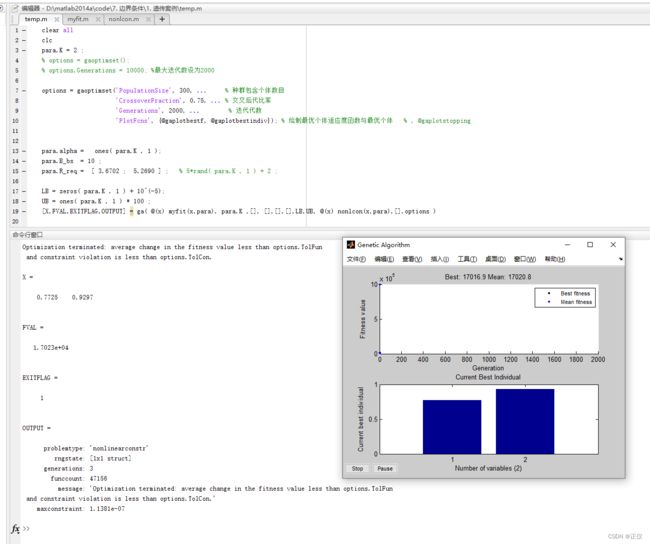
由此可知,增大种群规模、扩大目标函数、增大迭代轮数等方法,确实可以减缓 exitflg=4 的情况。
五、最终代码
解决了该问题后,本篇博客文末附上最终代码:
1. 主函数:
clear all
clc
para.K = 8 ;
% options = gaoptimset('PopulationSize', 100, ... % 种群包含个体数目
% 'CrossoverFraction', 0.75, ... % 交叉后代比率
% 'Generations', 2000, ... % 迭代代数
% 'TolFun',10^(-2), ...
% 'TolCon',10^(-2), ...
% 'PlotFcns', {@gaplotbestf, @gaplotbestindiv}); % 绘制最优个体适应度函数与最优个体 % , @gaplotstopping
para.alpha = ones( para.K , 1 );
para.B_bs = 10 ;
para.R_req = 5*rand( para.K , 1 ) + 2 ; % [ 3.6702 ; 5.2690 ] ; %
LB = zeros( para.K , 1 ) + 0.1;
UB = ones( para.K , 1 ) * 100 ;
[X,FVAL,EXITFLAG,OUTPUT] = ga( @(x) myfit(x,para), para.K ,[], [],[],[],LB,UB, @(x) nonlcon(x,para),[])
% [X,FVAL,EXITFLAG,OUTPUT] = ga( @(x) myfit(x,para), para.K ,[], [],[],[],LB,UB, @(x) nonlcon(x,para),[],options )
2. 目标函数:
function f = myfit( x , para )
f = sum(x);
end
3. 非线性约束函数:
function [ g , h ] = nonlcon( x , para )
g = sum( para.R_req ./ log2( 1 + para.alpha .* x' ) ) - para.B_bs;
h=[] ;
运行结果: