【数据结构入门精讲 | 第四篇】考研408、企业面试表专项习题
在上一篇中我们介绍了表的相关概念,这篇文章我们进行表的专项练习。
目录
-
- 顺序表判断题
- 顺序表选择题
- 顺序表编程题
-
- R6-1 线性表元素的区间删除
- R7-1 数组循环左移
- R7-1 最长连续递增子序列
- R7-2 求链式线性表的倒数第K项
- 链表判断题
- 链表选择题
- 链表填空题
- 链表函数题
-
- R6-1 单链表分段逆转
- 链表编程题
-
- R7-1 喊山
顺序表判断题
1.对于顺序存储的长度为N的线性表,删除第一个元素和插入最后一个元素的时间复杂度分别对应为O(1)和O(N)。(错)
解析:删除第一个元素需要将数组中的所有元素向前移动一位,以填补删除元素所占用的位置。因此,时间复杂度为O(N)。
void delete_first_element(int *arr, int n) {
for (int i = 0; i < n - 1; i++) {
arr[i] = arr[i+1];
}
arr[n-1] = 0;
}
插入最后一个元素只需要将新元素添加到数组的末尾即可,时间复杂度为O(1)
for (int i = 0; i < len; i++) {
new_arr[i] = arr[i];
}
new_arr[len] = element;
2.在N个结点的顺序表中访问第i(1<=i<=N)个结点和求第i(2<=i<=N)个结点直接前驱的算法时间复杂度均为O(1)。(对)
解析如下:
printf("%d %d", arr[i - 1], arr[i - 2]);
3.顺序存储方式的优点是存储密度大,且插入、删除运算效率高。 (错)
解析:顺序存储方式存储密度大但插入删除效率低。
4.对于顺序存储的长度为N的线性表,访问结点和增加结点的时间复杂度分别对应为O(1)和O(N)。(对)
解析:在插入操作时,需要将插入位置后面的元素都向后移动,以便为新元素腾出空间
5.在用数组表示的循环队列中,front值一定小于等于rear值。(错)
顺序表选择题
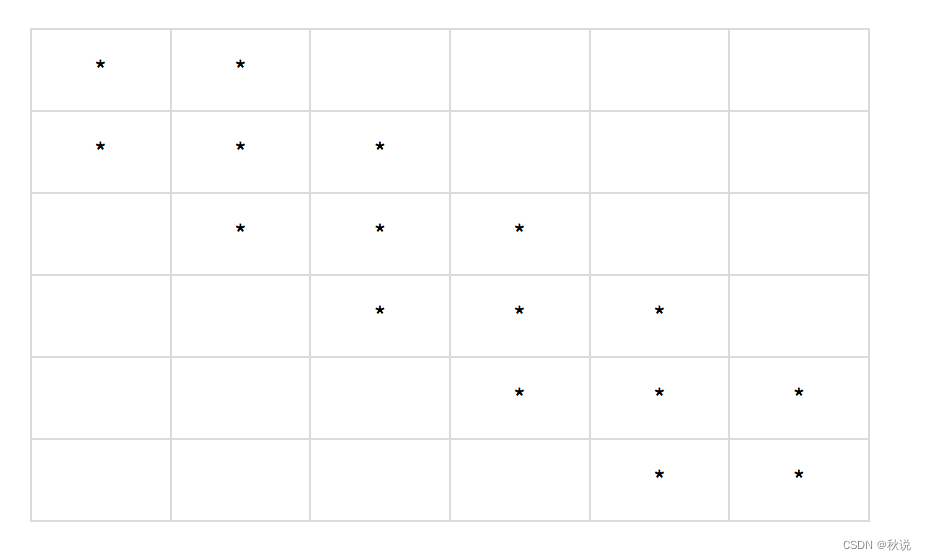
三对角矩阵除了第一行和最后一行是每行2个元素外,中间的每行都是三个元素。m30,30对应的元素序号为:2(第一行2个元素)+28*3+2(最后一行2个元数)=88,在数组中下标为87。
2.稀疏矩阵采用三元组存储的时候,一般需要一个行逻辑链接的顺序表,用以指出每一行的第一个非零元素在三元组中的位置。用这个顺序表的主要目的是为了_ C_。
A.更清晰表示每列元素所在位置
B.更清晰表示每行元素所在位置
C.加快算法运行效率
D.节省存储空间
解析:使用行逻辑链接的顺序表可以加快对稀疏矩阵的操作和处理速度,从而提高算法的运行效率。这个顺序表可以帮助快速访问每一行的非零元素,减少不必要的遍历和搜索操作,从而节省时间。
3.在包含 n 个数据元素的顺序表中,▁▁B▁▁ 的时间复杂度为 O(1)。
A.将 n 个元素按升序排序
B.访问第 i(1≤i≤n) 个数据元素
C.在位序 i(1≤i≤n+1) 处插入一个新结点
D.删除位序 i(1≤i≤n) 处的结点
4.已知二维数组 A 按行优先方式存储,每个元素占用 1 个存储单元。若元素 A[0][0] 的存储地址是 100,A[3][3] 的存储地址是 220,则元素 A[5][5] 的存储地址是:选D
A.301
B.295
C.306
D.300
解析:由A[0][0]和A[3][3]的存储地址可知A[3][3]是二维数组A中的第121个元素,假设二维数组A的每行有n个元素,则n x 3 + 4 = 121,n=39
所以元素 A[5][5] 的存储地址是100 + 39 * 5 + 6 -1 = 300
5.对于顺序存储的长度为N的线性表,访问结点和增加结点的时间复杂度为:C
A.O(1), O(1)
B.O(N), O(N)
C.O(1), O(N)
D.O(N), O(1)
6.若在含n个元素的顺序表中执行删除操作,设删除每个元素的概率相同,则该删除操作需移动元素的平均次数为 (n-1)/2。
解析:
要删除的个数从1~n
如果删除最后一个,则不需要移动
删除倒二个,则移动一次
删除第一个,则移动n-1次
所以一共移动(n-1)*n/2次
再除以n
 解析:可以找n+1个位置插入
解析:可以找n+1个位置插入
如果插入到最后一个后面,则不需要移动
插入到倒二个后面,则移动一次
插入到倒三个后面,则移动二次
所以一共移动(n+1)*n/2次
再除以n+1
8.在带哨兵结点的双循环链表中,设链结点的后继指针域为next,前驱指针域为prior,指针header指向哨兵结点,则判断该链表是否为空的表达式为:
header->next==header 或 header->prior==header
顺序表编程题
R6-1 线性表元素的区间删除
给定一个顺序存储的线性表,请设计一个函数删除所有值大于min而且小于max的元素。删除后表中剩余元素保持顺序存储,并且相对位置不能改变。
函数接口定义:
List Delete( List L, ElementType minD, ElementType maxD );
其中List结构定义如下:
typedef int Position;
typedef struct LNode *List;
struct LNode {
ElementType Data[MAXSIZE];
Position Last; /* 保存线性表中最后一个元素在数组中的位置 */
};
L是用户传入的一个线性表,其中ElementType元素可以通过>、==、<进行比较;minD和maxD分别为待删除元素的值域的下、上界。函数Delete应将Data[]中所有值大于minD而且小于maxD的元素删除,同时保证表中剩余元素保持顺序存储,并且相对位置不变,最后返回删除后的表。
裁判测试程序样例:
#include 输入样例:
10
4 -8 2 12 1 5 9 3 3 10
0 4
输出样例:
4 -8 12 5 9 10
List Delete(List L,ElementType minD,ElementType maxD)
{
int j=0;
int k=L->Last;//最后一个元素的位置
for(int i=0;i<=k;i++)
{
if(L->Data[i]<=minD||L->Data[i]>=maxD)
{
//如果该数应该被保留,则复制到新的线性表
L->Data[j]=L->Data[i];
j++;
}
else
{
//如果该数应该被删除
//将原线性表的最后一个元素复制到当前位置i,同时将原线性表的最后一个元素的索引k减1
//相当于删除了当前元素
L->Last--;
}
}
}
R7-1 数组循环左移
本题要求实现一个对数组进行循环左移的简单函数:一个数组a中存有n(>0)个整数,在不允许使用另外数组的前提下,将每个整数循环向左移m(≥0)个位置,即将a中的数据由(a0a1⋯an−1)变换为(am⋯an−1a0a1⋯am−1)(最前面的m个数循环移至最后面的m个位置)。如果还需要考虑程序移动数据的次数尽量少,要如何设计移动的方法?
输入格式:
输入第1行给出正整数n(≤100)和整数m(≥0);第2行给出n个整数,其间以空格分隔。
输出格式:
在一行中输出循环左移m位以后的整数序列,之间用空格分隔,序列结尾不能有多余空格。
输入样例:
8 3
1 2 3 4 5 6 7 8
输出样例:
4 5 6 7 8 1 2 3
#include R7-1 最长连续递增子序列
给定一个顺序存储的线性表,请设计一个算法查找该线性表中最长的连续递增子序列。例如,(1,9,2,5,7,3,4,6,8,0)中最长的递增子序列为(3,4,6,8)。
输入格式:
输入第1行给出正整数n(≤105);第2行给出n个整数,其间以空格分隔。
输出格式:
在一行中输出第一次出现的最长连续递增子序列,数字之间用空格分隔,序列结尾不能有多余空格。
输入样例:
15
1 9 2 5 7 3 4 6 8 0 11 15 17 17 10
输出样例:
3 4 6 8
#include R7-2 求链式线性表的倒数第K项
给定一系列正整数,请设计一个尽可能高效的算法,查找倒数第K个位置上的数字。
输入格式:
输入首先给出一个正整数K,随后是若干非负整数,最后以一个负整数表示结尾(该负数不算在序列内,不要处理)。
输出格式:
输出倒数第K个位置上的数据。如果这个位置不存在,输出错误信息NULL。
输入样例:
4 1 2 3 4 5 6 7 8 9 0 -1
输出样例:
7
#include 链表判断题
1.链表是一种随机存取的存储结构。(错)
解析:链表的顺序访问是通过从头节点开始,依次遍历链表的节点来实现的,即链式存储结构。
数组是一种随机存取的存储结构,可以通过索引直接访问数组中的任意元素。
2.线性表L如果需要频繁地进行不同下标元素的插入、删除操作,此时选择顺序存储结构更好。(错)
解析:由于链式存储结构在插入和删除操作时不需要移动大量元素,只需修改指针连接,因此更适合频繁变动的情况。
3.在具有N个结点的单链表中,访问结点和增加结点的时间复杂度分别对应为O(1)和O(N)。(错)
解析:访问结点的时间复杂度为O(N),增加结点的时间复杂度为O(1)。
4.若用链表来表示一个线性表,则表中元素的地址一定是连续的。(错)
解析:链表中的节点可以在内存中的任意位置,它们通过指针连接起来形成链表结构。
使用数组来表示线性表时,数组中的元素是连续存储的。
5.将N个数据按照从小到大顺序组织存放在一个单向链表中。如果采用二分查找,那么查找的平均时间复杂度是O(logN)。(错)
如果是存放在数组中,则是对的。但由于在链表中,所以不会是logn
6.对于单循环链表,表空的表达式为header->next==header。(对)
链表选择题
1.假设某个带头结点的单链表的头指针为head,则判定该表为空表的条件是( D )
A.head= =NULL
B.head!=NULL
C.head->next= =head
D.head->next= =NULL
解析:在带头结点的单链表中,如果链表为空表,头结点的下一个指针head->next指向的也应为空。
3.在具有N个结点的单链表中,实现下列哪个操作,其算法的时间复杂度是O(N)? 选B
A.在地址为p的结点之后插入一个结点
B.遍历链表和求链表的第i个结点
C.删除地址为p的结点的后继结点
D.删除开始结点
解析:遍历链表需要按顺序访问每个结点,因此时间复杂度为O(N)。而求链表的第i个结点也需要遍历i个结点,所以同样具有O(N)的时间复杂度。
选项 A. 在地址为p的结点之后插入一个结点 的操作只需要修改指针连接,时间复杂度为O(1)。 选项 C. 删除地址为p的结点的后继结点 的操作也只需要修改指针连接,时间复杂度为O(1)。 选项 D. 删除开始结点的操作只需要修改头指针的指向,时间复杂度为O(1)。
选C,解析:要实现两个多项式的乘法,需要让一个多项式的每一项乘以另外一个多项式的每一项,因此这个题目的时间复杂度只跟非零项的个数有关,与最高项的指数无关。
5.已知指针ha和hb分别是两个单链表的头指针,下列算法将这两个链表首尾相连在一起,并形成一个循环链表(即ha的最后一个结点链接hb的第一个结点,hb的最后一个结点指向ha),返回ha作为该循环链表的头指针。请将该算法补充完整。
typedef struct node{
ElemType data;
struct node *next;
}LNode;
LNode *merge(LNode *ha, LNode *hb) {
LNode *p=ha;
if (ha==NULL || hb==NULL) {
cout<<”one or two link lists are empty!”<<endl;
return NULL;
}
while ( p->next!=NULL )
p=p->next;
p->next=hb;
while ( p->next!=NULL )
p=p->next;
_____A_____
}
A.p->next=ha; return ha;
B.ha=p->next; return p;
C.p->next=ha; return p;
D.ha=p->next; return ha;
选A,解析:在补充完整算法的过程中,首先让p指针遍历到链表ha的末尾,然后将ha的末尾指针指向hb的头部,形成循环链表。最后返回ha作为该循环链表的头指针。
6.对于一非空的循环单链表,
h和p分别指向链表的头、尾结点,则有:选C
A.p->next == NULL
B. p == h
C.p->next == h
D.p == NULL
解析:对于非空的循环单链表,尾结点的指针域应该指向头结点,即p->next == h
7.双链表的结点类型定义如下:
typedef struct node *link; //双链表结点指针类型
typedef struct node {// 双链表结点类型
ListItem element;//表元素
link left,//链表左结点指针
right;//链表右结点指针
}Node;
在双向链表存储结构中,删除 p 所指的结点,相应语句为:( )
A.p->right->left=p; p->right=p->right->right;
B.p->right=p->left->left; p->left=p->right->right;
C.p->left->right=p->right; p->right->left=p->left;
D.p->left=p->left->left; p->left->right=p;
解析:选C,画图即可
left-A-right left-p-right left-b-right
8.链表具有的特点是(D)。
A.可随机访问任意一个元素
B.要事先估计存储空间
C.插入删除需要移动元素
D.所需空间与线性表长度成正比
解析:A,不可。B,不需要。C,只要移动指针。D,对。
9.在单链表指针为p的结点之后插入指针为s的结点,正确的操作是__B__。
A.p->next=s;s->next=p->next
B.s->next=p->next;p->next=s
C.P->next=s;p->next=s->next
D.P->next=s->next;p->next=s
10.在需要经常查找结点的前驱与后继的场合中,使用( B )比较合适。
A.单链表 B.双链表 C.顺序表 D.循环链表
11.用链接方式存储的队列,在进行插入运算时( D ).
A. 仅修改头指针 B. 头、尾指针都要修改
C. 仅修改尾指针 D.头、尾指针可能都要修改
12.下列关于静态链表的说法错误的是( C )。
A、多条静态链表可共用一个数组空间
B、在数组空间中,静态链表中的元素可以随机存放
C、静态链表可以无限扩充
D、静态链表的指针域也称为游标,存放下一元素在数组中的下标
链表填空题
(pre)p(next) 与 (pre)q(next)是双向指向的
要在两者之间插入新的节点x,怎么操作?
解析:
x->pre=p
x->next=p->next
p->next->pre=x
p->next=x
下列代码的功能是返回带头结点的单链表L的逆转链表。
List Reverse( List L )
{
Position Old_head, New_head, Temp;
New_head = NULL;
Old_head = L->Next;
while ( Old_head ) {
Temp = Old_head->Next;
;//Old_head->Next = New_head
New_head = Old_head;
Old_head = Temp;
}
;//L->Next = New_head
return L;
}
解析:代码注释如下
List Reverse( List L )
{
Position Old_head, New_head, Temp;
New_head = NULL; // 初始化新链表头节点指针为NULL
Old_head = L->Next; // 保存原链表头节点的下一个节点
while ( Old_head ) {
Temp = Old_head->Next; // 保存当前节点的下一个节点
Old_head->Next = New_head; // 将当前节点的Next指针指向新链表的头节点
New_head = Old_head; // 更新新链表的头节点为当前节点(将当前节点插入到新链表的头部)
Old_head = Temp; // 将当前节点移动到下一个节点
}
L->Next = New_head; // 将原链表的头节点指向新链表的头节点
return L; // 返回反转后的链表头节点指针
}
链表函数题
R6-1 单链表分段逆转
给定一个带头结点的单链表和一个整数K,要求你将链表中的每K个结点做一次逆转。例如给定单链表 1→2→3→4→5→6 和 K=3,你需要将链表改造成 3→2→1→6→5→4;如果 K=4,则应该得到 4→3→2→1→5→6。
函数接口定义:
void K_Reverse( List L, int K );
其中List结构定义如下:
typedef struct Node *PtrToNode;
struct Node {
ElementType Data; /* 存储结点数据 */
PtrToNode Next; /* 指向下一个结点的指针 */
};
typedef PtrToNode List; /* 定义单链表类型 */
L是给定的带头结点的单链表,K是每段的长度。函数K_Reverse应将L中的结点按要求分段逆转。
裁判测试程序样例:
#include 输入样例:
6
1 2 3 4 5 6
4
输出样例:
4 3 2 1 5 6
代码如下:
void K_Reverse(List L,int K)
{
List H=L;
PtrToNode p,q,w,t;//定义指针
int num;//用于计数
while(H)//遍历整个链表
{
num=0;
p=H;//p指向当前待翻转的第一个节点
//找到需要翻转的K个节点
while(num<K&&p->Next)
{
num++;
p=p->Next;
}
if(num<K)
return;//如果不足K个节点,则退出循环
else
{
//对这K个节点进行翻转操作
t=H->Next;//t指向待翻转区间的前驱节点
w=p->Next;//w指向待翻转区间的后继节点
p->Next=null;//将待翻转区间的后继节点置为Null,便于后面插入节点
//将待翻转的每个节点插入到头部节点之后
p=H->Next;
while(p)
{
q=p;//q指向当前待插入的节点
p=p->Next;
q->Next=H->Next;//将该节点插入到头部节点之后
H->Next=q;
}
//连接待翻转区间的前驱节点和后继节点
t->Next=w;
//将指针H指向下一个待翻转区间的头部节点
H=t;
}
}
}
链表编程题
R7-1 喊山
喊山,是人双手围在嘴边成喇叭状,对着远方高山发出“喂—喂喂—喂喂喂……”的呼唤。呼唤声通过空气的传递,回荡于深谷之间,传送到人们耳中,发出约定俗成的“讯号”,达到声讯传递交流的目的。原来它是彝族先民用来求援呼救的“讯号”,慢慢地人们在生活实践中发现了它的实用价值,便把它作为一种交流工具世代传袭使用。
一个山头呼喊的声音可以被临近的山头同时听到。题目假设每个山头最多有两个能听到它的临近山头。给定任意一个发出原始信号的山头,本题请你找出这个信号最远能传达到的地方。
输入格式:
输入第一行给出3个正整数n、m和k,其中n(≤10000)是总的山头数(于是假设每个山头从1到n编号)。接下来的m行,每行给出2个不超过n的正整数,数字间用空格分开,分别代表可以听到彼此的两个山头的编号。这里保证每一对山头只被输入一次,不会有重复的关系输入。最后一行给出k(≤10)个不超过n的正整数,数字间用空格分开,代表需要查询的山头的编号。
输出格式:
依次对于输入中的每个被查询的山头,在一行中输出其发出的呼喊能够连锁传达到的最远的那个山头。注意:被输出的首先必须是被查询的个山头能连锁传到的。若这样的山头不只一个,则输出编号最小的那个。若此山头的呼喊无法传到任何其他山头,则输出0。
输入样例:
7 5 4
1 2
2 3
3 1
4 5
5 6
1 4 5 7
输出样例:
2
6
4
0
#include 以上就是本篇文章的全部内容,下一篇文章中我们将介绍栈的相关知识点。