南京大学-软件分析-课程05-数据流分析基础理论

1. 从另一个角度看迭代算法

用k个值来表示CFG中的k个节点，在每一轮迭代中更新对应的值。
迭代函数为$F:V^k$—>$V^k$

X is a fixed point of function F if X = F(X)

2. Partial Order（偏序）

当我们定义偏序集（partially ordered set，poset）时，我们将其表示为一个二元组 r (P, ⊑)，其中 ⊑是一个二元运算符在P上定义偏序关系。有如下属性：
(1) ∀x ∈ P, x ⊑ x (Reflexivity)
(2) ∀x, y ∈ P, x ⊑ y ∧ y ⊑ x ⟹ x = y (Antisymmetry)
(3) ∀x, y, z ∈ P, x ⊑ y ∧ y ⊑ z ⟹ x ⊑ z (Transitivity)

例子：
整数集上小于等于关系。
字符串的子串关系。
集合的子集关系。

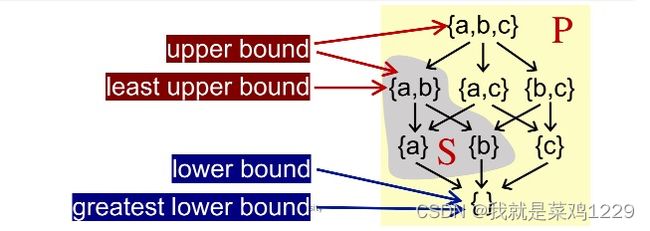
3. Upper and Lower Bounds(上下界)

Given a poset (P, ⊑) and its subset S that S ⊆ P, we say that
u ∈ P is an upper bound of S, if ∀x ∈ S, x ⊑ u. Similarly,
l ∈ P is an lower bound of S, if ∀x ∈ S, l ⊑ x.

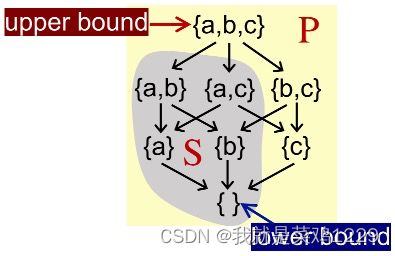
最小上界

我们定义S的最小上界least upper bound (lub or join)， 记为 ⊔S,
对于S是每个上界u，有 ⊔S ⊑ u.

最大下界

我们定义S的大下界greatest lower bound (glb, or meet)， 记为 ⊓S,
对于S是每个下界l，有 l ⊑ ⊓S.

一般来说，如果S包含两个元素a和b。
⊔S can be written a ⊔ b (the join of a and b)，a和b的最小上界。
⊓S can be written a ⊓ b (the meet of a and b)，a和b的最大下界。

一些属性

• 不是每个偏序集都有最小上界（lub/join）和最大下界（glb/meet）。
• 如果有lub或glb，则一定唯一。

4. Lattice，Semilattice，Complete and Product Lattice（格、半格）

Lattice

Given a poset (P, ⊑), ∀a, b ∈ P, if a ⊔ b and a ⊓ b exist, then (P, ⊑) is called a lattice
偏序集中任意两个元素都存在最大下界/最小上界。则这个偏序集可以被称为Lattice

Semilattice

对于最大下界/最小上界只存在一个的情况下，称之为半个，
Given a poset (P, ⊑), ∀a, b ∈ P,
if only a ⊔ b exists, then (P, ⊑) is called a join semilattice
if only a ⊓ b exists, then (P, ⊑) is called a meet semilattice

Complete Lattice

Given a lattice (P, ⊑), for arbitrary subset S of P, if ⊔S and ⊓S exist, then (P, ⊑) is called a complete lattice
一个Lattice中的所有子集都有都有一个最小上界和一个最大下界。
Every complete lattice (P, ⊑) has
a greatest element T = ⊔P called top and
a least element ⊥ = ⊓P called bottom

每一个有限元素的lattice都是一个Complete Lattice

Product Lattice

Given lattices $L_1$ = ($P_1$, ${⊑}_1$), $L_2$ = ($P_2$, ${⊑}_2$), …, $L_n$ = ($P_n$, ${⊑}_n$), if for all i,($P_i$, ${⊑}_i$)has ${\bigsqcup }_i$ (least upper bound) and ${\sqcap }_i$ (greatest lower bound), then
we can have a product lattice $L_n$ = (P, ⊑) that is defined by:

• product lattice 也是一个lattice
• 如果product lattice是一个complete的product，则这个product lattice也是complete的

5. 通过Lattice来进行数据流分析

一个数据流分析框架（D, L, F）包括：
D：数据流的方向，可以是前向（forwards）或后向（backwards）。
L：包括值域 V 和 meet ⊓ 或 join ⊔ 操作符的格（lattice）。
F：从 V 到 V 的转移函数（每个节点可能有自己的转移函数，也可能一样）。

回答以下问题

迭代算法（或称为IN/OUT方程系统）产生数据流分析的解决方案：

• 该算法是否保证终止或达到固定点，或者它总是有解吗？
• 如果是的话，解是否唯一，或者只有一个固定点？如果存在多个解，我们的解是否是最佳的（最精确的）？
• 该算法何时会达到固定点，或者我们何时可以得到解决方案？

6.单调性和不动点原理

单调性

A function f: L → L (L is a lattice) is monotonic if ∀x, y ∈ L,x ⊑ y ⟹ f(x) ⊑ f(y)

不动点原理

Given a complete lattice (L, ⊑), if
(1) f: L → L is monotonic and
(2) L is finite,
then
the least fixed point of f can be found by iteratingf(⊥), f(f(⊥)), …, $f^k(\perp )$ until a fixed point is reached
the greatest fixed point of f can be found by iteratingf(T), f(f(T)), …, $f^k(T)$ until a fixed point is reached

证明：

有限单调全格。
证明：能达到最大不动点
通过定义一个函数的最大下界⊥和转移函数f：L–>L，我们有⊥ ⊑ f(⊥)。
由于单调，可以得出f(⊥) ⊑ f(f(⊥)) = $f^2$(⊥)
重复f，得到⊥ ⊑ f(⊥) ⊑ $f^2$(⊥) ⊑ … ⊑ $f^i$(⊥)
因为L是有限的（假设高度为H），因此值在 ⊥、f(⊥)、$f^2$(⊥) 到 $f^H$(⊥) 之间有界。
当 i > H 时，根据鸽笼原理，存在 k 和 j，使得 $f^k$(⊥) = $f^j$(⊥)（假设 k < j ≤ H+1）。
进一步，由于 $f^k$(⊥) ⊑ … ⊑ $f^j$(⊥)（f 的单调性），我们有 $f^{Fix}$ = $f^k$(⊥) = $f^{k+1}$(⊥) = … = $f^j$(⊥)（反证法证明）。

鸽笼原理：鸽笼原理（Pigeonhole Principle）是一种基本的数学原理，它描述了分配物品到有限数量的容器时的一种必然性。简而言之，如果你要将 n 个物品放入不超过 m 个容器中，而 n 大于 m，那么至少有一个容器必然会包含两个或更多的物品。

由于L是有限元素，这里假设为H。如果在前H次没有到达不动点，则根据单调性此时$f^H$应该为最大值，则下一次$f^{H+1}$应该等于$f^H$，否则将违背单调性。