二叉树进阶题目(超详解)
文章目录
- 前言
- 根据二叉树创建字符串
-
- 题目
- 分析
- 写代码
- 二叉树的层序遍历
-
- 题目
- 分析
- 写代码
- 二叉树的层序遍历II
-
- 题目
- 分析
- 写代码
- 二叉树的最近公共祖先
-
- 题目
- 分析
- 写代码
- 时间复杂度
- 优化思路
-
-
- 优化的代码
-
- 二叉搜索树与双向链表
-
- 题目
- 分析
- 写代码
- 从前序与中序遍历序列构造二叉树
- 题目
- 分析
- 写代码
- 从中序与后序遍历序列构造二叉树
- 二叉树的前序遍历
-
- 题目
- 分析
- 写代码
- 中序的非递归
-
- 分析
- 写代码
- 后序的非递归
-
- 分析
- 写代码
前言
二叉树进阶的题目不一定更复杂,但一定更适合用C++去写。
这里的题目用C语言去做会非常恶心。
根据二叉树创建字符串
题目链接
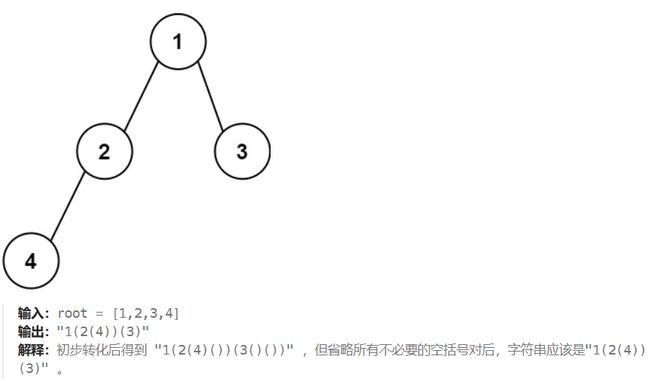
题目
要求很简单,就是用括号把左右子树括起来。
就是递归左子树之前加一个左括号,左子树递归完了加一个右括号
每棵树都这样子就搞定了
分析
这里还有一个新的问题:
要去省略不必要的括号

哪些括号可以省略呢?
观察一下。

写代码
假设我们不考虑括号解决这个问题
其实就是一个前序,但又是一个后序拿结果的问题。
现在我们怎么解决一下,把省略的问题给解决一下?
可以分为三种情况去判断,但能不能更简洁一些。
左为空分两种情况,如果右不为空就不省略,右为空就省略,
所以我们这里考虑加情况判断。
如果右为空。
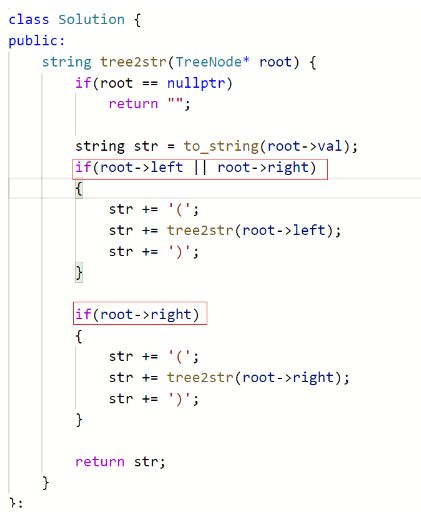
这连个if条件写的还是非常巧妙的。
这样更简洁一些。
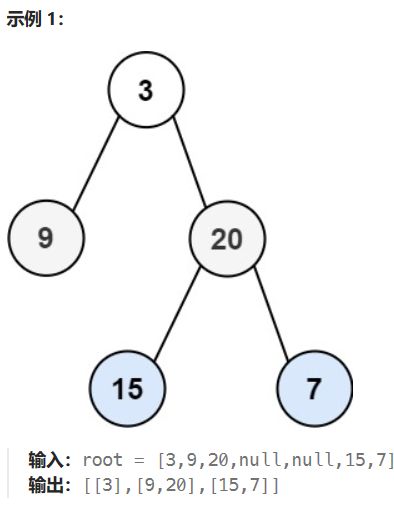
二叉树的层序遍历
题目链接
题目
分析
它要求要层序遍历没有问题,但是它要一层一层返回。
相当于要放到一个二维数组里面。
我们用C++就不用担心上面的东西,因为C++里有vector的vector
当然vector的vector传值返回代价很大,但是不用担心,C++11会有
右值引用能解决这个问题。

怎么样一行一行控制呢
第一种思路:
一个对列控制结点的指针然后去控制层序遍历。
一个对列存整型,表示它是第几层的
知道它是第几层就可以依次往二维数组,vector的vector里放。
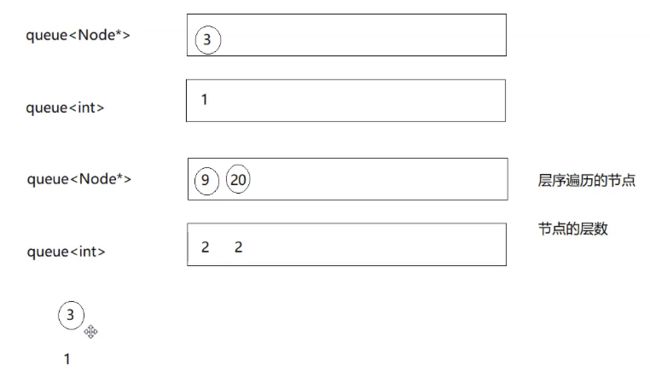
第二种思路
就用一个队列来完成
增加一个变量去记录这一层的数据个数,然后去控制一层一层出。
我们队列里面同时可能有两层的数据。
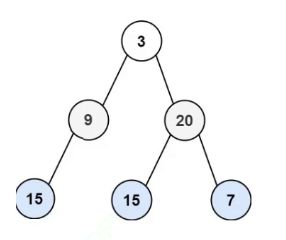
3出来带9和20,9出来带15.
9出来的时候队列里面同时有两层的数据,有时候有一层,有时候有两层。
怎样控制一层一层出?
根进去的时候
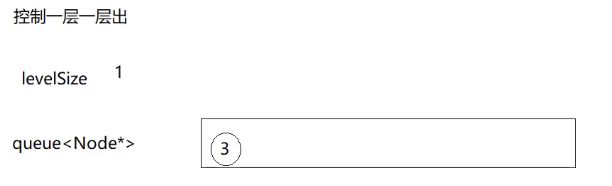
levelSize是1,表示这一层只有一个。
然后出第一层,levelSize–,减到0就表示出完了。
出的同时会把它的孩子带进去。
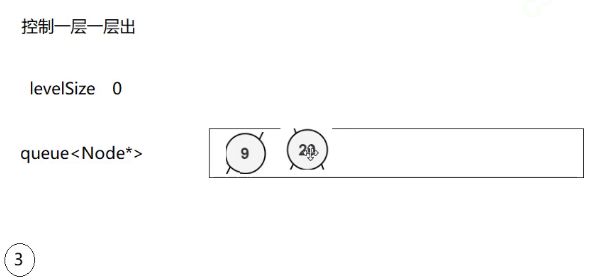
当前层出完了,一定意味着下一层都进对列了
这个时候重新更新下一层的数据个数,队列里面有几个就几个。这个时候leveSIze由0变成2
我们通过levelSize这个变量来控制一层一层出

第二层出完了,说明第三次层都在最里面。这跟上面的思路一样了。
第一种思路比第二种思路还能更简洁一点,这个地方只有一个队列。
第二种有两个队列还要控制对应的数据放大vector里去,更麻烦一些。
写代码
根先进队列,注意要处理一下根为空的情况

接下来
控制一层一层出

二叉树的层序遍历II
我们接着来看上一道题目的变形题
题目链接
题目
分析
这个题目也是层序遍历,但是要求自底向上。
也就是先拿倒数第一层再拿倒数第二层。
怎么办?
这个题目最简单的方式就是把刚才的代码拷贝一份过来。
逻辑上不变,把它逆置一下就可以了。
写代码
二叉树的最近公共祖先
题目链接
这个题目是超级经典的题目
这个题目展示了很多的一些技巧
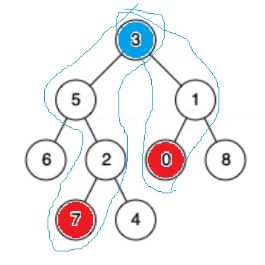
题目
分析
什么是公共祖先?
从我到根节点路径下的结点都是我的祖先。
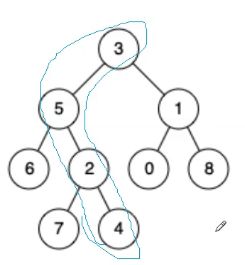
7和0的最近公共祖先是谁?

7和4的最近公共祖先是谁?
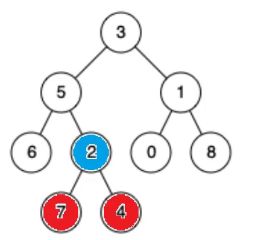
最疑惑的地方来了。
5和4的公共祖先是谁?
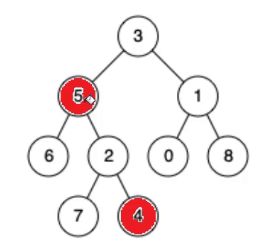
是3还是5

思路一:
这道题本质可以理解成链表相交。
如果三叉链(每个结点有parent), 就是链表相交的问题
链表相交挺简单的。
知道两个结点的指针p和q,沿着parent往上走就可以了。
链表相交怎么求交点?
首先求长度,然后长的先走,然后同时走。
相等结点地址相等的那个就是交点。
思路二:
直接找公共祖先怎么找?
仔细观察
这个公共祖先有一个特征:
如果一个在我的左子树,一个在我的右子树,我就是公共祖先
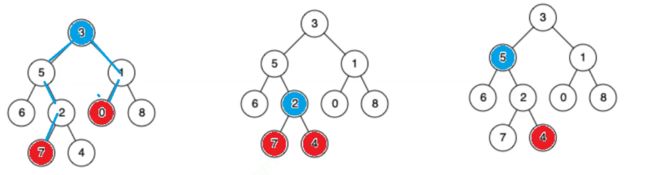
第一个最简单,一进来就找到了。
第二个,一进来,都是祖先但不是公共祖先,这两个结点都在我的左。
这个时候公共祖先不可能在右树。所以递归到我的左数去找。
依次往下走,直到这两个结点一个在我的左,一个在我的右,就是公共祖先。
这种玩法跟搜索二叉树类似,但搜索二叉树更简单直接比较。
这里要看两个结点分别在我的左树还是右树
第三个,根就是其中之一的结点,就不用往下递归了。
写代码
这里有一个确定的点。
下面写的代码非常的关键
有没有一种情况,p或者q就是我的根。
有可能,下面。
![]()

接下来确定这两个结点时在左树还是右树
下面的代码很关键

这是我们之前讲过的。
接下来,如果两个结点都在我的左,子问题:转换成去我的左树去找。


右边也是一样。
这个算法能过,但是时间消耗很慢。
这道题最精华的部分是在控制pInLeft,pInRight,如果控制不好写起来很痛苦,如果控制好了写起来很舒服。
时间复杂度
思路二的时间复杂度是多少:
O(N^2)
这里要注意,不要这样以为,每一次确定在左树还是右树是O(N),然后往下走是logN层,然后时间复杂度是N*lgN
但是达不到N*logN,这里不能认为高度是logN,只有满二叉树和完全二叉树是logN,这里没有说它是满二叉树和完全二叉树。
像这种情况,这里面会有大量的重复查找。
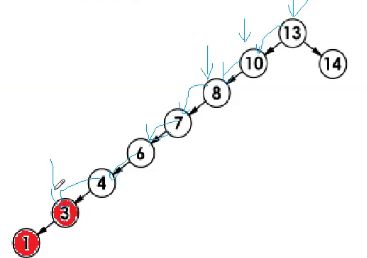
这里递归走过程就相当于一个等差数列。
面对这种情况呢就是O(N^2)
优化思路
思路二:
如果是搜索二叉树可以优化到O(N),
注意搜索二叉树 也有歪脖子的情况。
搜索二叉树不需要IsInTree();

每次确定都是O(1),最多走N次了。不需要查找。
但是这道题非常可惜不是搜索二叉树。
如果不是搜索二叉树,要求优化到O(N)怎么办呢?
有一种取巧的思路,复制这棵树,复制成三叉链的。
节点给重新定义,这样是O(N),再去求还是O(N).
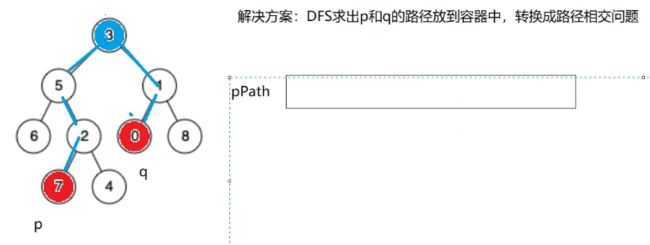
这里推荐大家用一个栈来存路径,求路径是O(N),求相交也是O(N),,整体就能控制到O(N)
如何求出p和q的路径?
树的DFS就是走深度优先遍历。
3先入栈,不管3是不是我要找的结点,如果是就return,3就是路径。
如果不是就往左边走,把5入栈,看5是不是,5不是我要的结点为什么要入栈。
5不是我要找的结点但是有可能是我要找的结点的路径的其中一个部分,所以要先入栈。一直走

没有找到就带个返回值回来。

现在这棵树就要处理了。怎么处理呢?
根的左子树没有我要的结点,根也不是我要找的结点,根的右子树没有我要的结点。
所以6不可能不是我要找的路径中的一个。
所以把6出栈,不让他影响我。同时要返回一个值给上一层,给上一层做一个参考。

回到5,说明左边都没有找到,这个时候怎么办呢?
下一步往右边去找。找到7以后怎么办?返回true,注意它不是直接返回给最外面,这个我们已经讲过很多次了。
2的左边找到了,就不需要往2的右边找了,直接返回true给上一层。(一定要返回true给上一层,不然把5出栈了)
5也是一样。
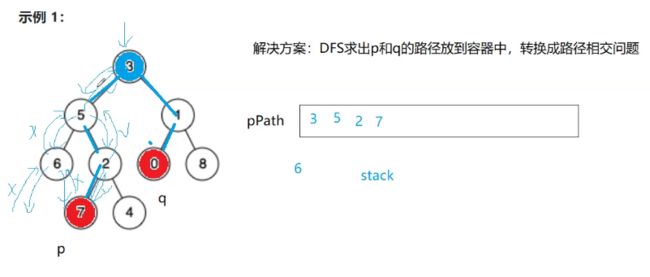
3的左边找到了也不需要往右边找,返回true.
这个时候就把路径给拿到了。
找出路径最坏的情况也就是把这棵树遍历一遍。
最后一件事就是相交了,以前链表需要求一下长度,现在不用求。
先让长的弹,谈到个数相等了,一起弹,同时判断相不相等。相等就是交点。
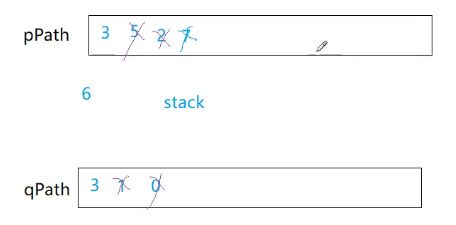
最坏的情况也是3*N,也是O(N)
这种方式唯一真正的问题在于,它需要栈的辅助空间。
上面的思路是这道题最经典的思路
这道题本质的大思路还是两种,要么判断在左右的特征来识别,要么路径相交。
优化的代码
重点是写这个GetPath
它必然要带返回值,只能做输出型参数去取了。

GetPath不用再判断返回值了,因为有提示,p和q一定在这棵树里面。

这道题具有非常强的启发性。
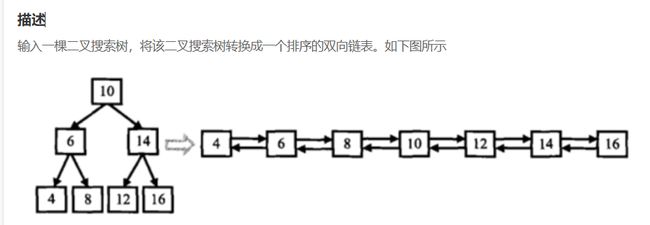
二叉搜索树与双向链表
题目链接
题目
分析
怎样把搜索二叉树转换成排序双向链表呢?
首先排序必然跟中序有关系。
这道题是很简单吗?中序遍历这棵树,
把值拿出来依次尾插,得到一个双向链表。
但是这里不一样,他要求在原树上操作

这道题也是一个非常经典的题目
可以可以回溯的时候链接父亲结点,链接父亲会坑,你要改成这个样子。
不能单纯的认为指向父亲指向谁这么简单。
怎么解决呢?
首先还是肯定跟中序有关系。
不要去关注是父亲还是爷爷还是谁,关注就会掉进坑里。
思路一:
如果借助一个容器来做这道题就太简单了,不用搞队列。

但是不符合这里的要求。
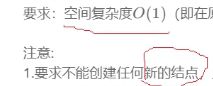
思路二:
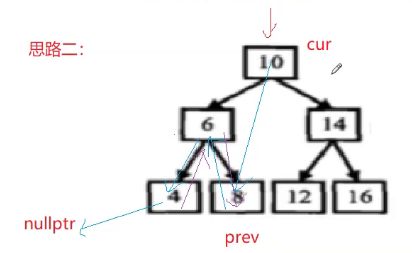
我们中序遍历这颗树同时记录一个前驱结点。
注意,任何一个结点的左一定是指向前驱的。

这里的关键关键结点在于后继如何解决?
你没有中序遍历过去的情况怎么知道后继在哪。
我在当前位置能改我的前驱,改不了我的后继,
但是我可以在下一步的时候再动手。
![]()
写代码
这道题最好写一个子函数,不然不好控制,稍不注意就会崩。
如果知道上面的思路还写不出来,说明递归还需要加强
有一种比较简单的方式,你可以先什么都不管,直接把中序先写出来。
但是在递归里面,prev得加引用,它没有往下递归就相当于是下一层栈帧了。
它不在循环出现了。
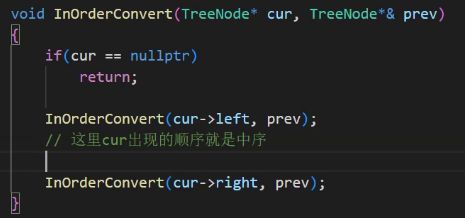

prev得加引用,cur再出现,就是在其他的栈帧里出现了,不是当前栈帧。
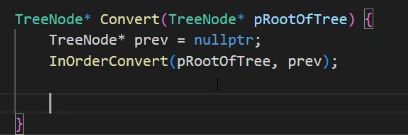
现在要返回链表的头,怎样返回链表的头呢?
可以提前找到最左结点找到这个头,也可以改完以后通过根这个结点一直向左递归。

这里真正难理解的就是cur是出现在不同栈帧里面的,画递归展开图就会发现。
从代码的角度,cur每次出现的顺序就是中序,但它不是在同一个函数里出现,它是在不同的递归栈帧里出现。
递归回来的时候让我指向前驱,前驱的后继指向我。
prev是在上一层栈帧改的,但是我的cur已经到下一层栈帧去了。
但是prev只有一个,所以得用引用。
从前序与中序遍历序列构造二叉树
题目链接
题目
分析
给了我们前序和中序。
首先分析一下,前序是什么?中序又是什么?

通过这样的特征我们就可以用中序来恢复这棵树,但是光有中序是不行的,
要借助前序来确定这里的根
首先3就是这里的根,就可以创建3了,

创建3之后就可以走一个前序去创建3的左子树
3的左子树被分割成左子树的中序区间。如果这个区间是空,就走右树。
如果这个区间不是空,下一个值一定是左子树的根。

再去创建9的左和右就没办法创建了,因为这个区间只有一个值,就代表它已经创建好了。
回来,链接上,然后开始递归它的右树。
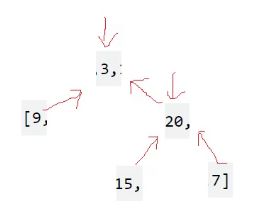
每次都要前序往后走去确定根。
这道题也没有其他技巧,就是前序确定根,中序分割左右子区间,
左右子区间决定要不要递归创建,继续分割左右子树。
多个值肯定要分割,只有一个值就不用分割了
写代码
这些题都有一个特点,不适合直接在原树上写。
前序得有一个下标一直往后走。
中序得是一段区间
![]()
首先不管其他的东西,前序这块首先就是创建根。
![]()
再继续往后走,在这个地方要分割出左右子区间
怎么分割呢?
要在中序里找根。
但是这道题有个前提,不能有值相同,不然就出问题了。
如果有值就会导致找根找不到。

rooti创建好了,现在要递归左子树。
现在要递归创建左子树,并且链在我的左边。

跟快排很像,其实本质上,这个模型跟快排是一样的。
现在就看唯一条件就是返回值。分割这个区间不断往下走,什么时候就不玩了呢?
这个区间有一个值还可以玩,如果不玩,就单独判断一下。
但是你要创建一个结点,把它的左右都置空,然后return.推荐继续玩。
从中序与后序遍历序列构造二叉树
如何通过中序和后序来处理这道题呢?
其实很简单,后序确定根,创建完跟之后,先创建右再创建左。
二叉树的前序遍历
题目链接
这道题我们以前用C语言写过,现在直接用vector就很简单了。
现在这道题我们要用迭代算法来完成这道题。
这道题如果用递归非常简单,现在用迭代时有一定的难度的。
题目
分析
先拿一颗稍复杂的树分析一下

这个用非递归不好搞在于哪里呢?
这道题用普通的改循环,已经不适用了。另外二叉树用非递归本来就不好搞。
先来分析一下前序

现在一直走根左子树,根左子树,根左子树一直走到是空结束。
剩下谁还没有玩呢?
如果一颗树分为根左子树,根左子树,根左子树,剩下哪个部分没有玩呢?
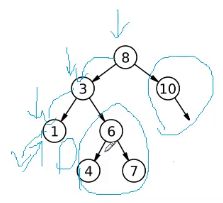
先访问1的右树,1的右树访问完了,1就完了。
1完了,1作为3的左树,然后访问3的右树。
这个思路有一个优势,这个掌握了,前序后序中序都可以用非递归实现
接下来又涉及一个问题,它的右子树怎么访问呢?
它又变成子问题了。所以非递归不是递归带式胜似递归,还是用递归的思路来玩的。

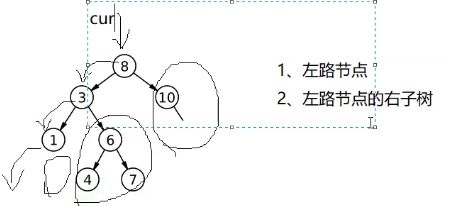
我们现在用图来展示一下非递归是如何访问一颗二叉树的
第一步:
先访问左路结点,同时要入栈,不入栈等下我们没办法处理它的右子树
因为我们要先访问1的右子树,然后3的,8的。

第二步:
第一个从栈里面出来的数据是1,然后访问1的右子树,1的右子树是空,没什么访问
再走一圈,栈里取到3,然后访问3的右子树
第三步
访问3的右子树怎么访问呢?
访问它的左路结点,然后左路结点入栈
大家看,每次循环都相当于在访问一颗树。

每次要取栈里面取到这个结点,然后访问它的右子树
这颗树是一个很复杂的树也没关系,继续入。
最后栈里取到10,然后访问它的右数,它的右树是空,没得访问,然后就结束了。
它不是用递归,但是它把右子树当作递归。
它不是之前的根,左子树,右子树,它是把一颗树分成左路结点和右子树,
这样循环才能走起来
任何一颗树分成左路结点,然后就剩下左路结点的右子树了。
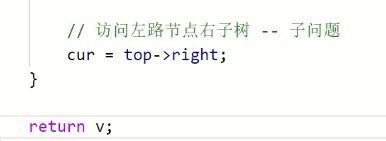
写代码
访问右子树
这里是关键的关键

很关键很关键,画图,把全部过程根据代码理解一下
什么时候循环结束呢?
这里有两个条件:
1.cur不为空
cur表示要访问一颗树的开始,
cur不为空表示有一颗树没有访问还得继续
2.栈不为空
栈不为空,表示还有结点的右子树没有被访问。
![]()
![]()
这个非递归是通用的,但是后序有一点点变化
二叉树的非递归不是递归但也是递归,而且是一个神奇的循环递归,
借助这个栈,跟快排也类似。
中序的非递归
无论前序还是后序中序都可以按照前面的思路,只是访问根的时机不一样。
因为本质都是一种DFS,都是一种深度优先遍历。
现在我们看一下中序
分析
cur指向一棵树表示要访问这个结点
只是前序是访问这个结点往左走,访问这个结点往左走,
现在走的是中序,中序得把左路访问完了再访问。
现在只能做一件事,把这些结点先入栈。

现在我们要访问右树,我们把栈里面把1取出来时候,能不能访问1?
可以,因为把这个1取出来之后意味着把它的左树访问完了,可以访问这个结点。
怎样访问它的右子树?
写代码
访问左路结点
cur不为空表示访问一颗树的开始,
这棵树有可能是空树,有可能是整棵树,有可能是我们拿到的左路结点的右树

访问

写完了,但是没过
![]()
没过的原因在哪里?
这里面是因为遇到空树就结束了。
1的右子树是空树就结束了。不符合我们的预期。

栈里面还有结点表示栈里面还有结点还有右子树没有访问
![]()
过了

后序的非递归
很多公司都只考后序,后序才是最难的,后序会了表示你前序中序都会了。
分析
后序怎么办?
根右左,然后把vector的数据逆置一下
这个思路好像可以,试一下
就相当于把前序改一下,但如果要边走边访问就不可以,打印也不行。
本质上是用了一个顺序性的取巧操作。
但是现在要求保持跟前序中序一样的思路呢?
先来分析一下,相比于前序中序的困境在哪里?
还是之前的左路结点,右子树。只是现在要把左路结点和右子树访问完了,
再访问根。
第一步:

入栈不访问。
从栈里面取到左路结点,意味着这个结点的左子树访问完了。
左子树访问完了还要访问右子树,右子树访问完了才能访问根。
第二步:
但是单拿这个1来说,栈里取到1的时候能直接访问1,因为1的右子树是空。
所以直接访问1.
这是第一种情况。
接着取到3,右不为空,不能直接访问,就访问它的右树的左路结点。
接着往下看
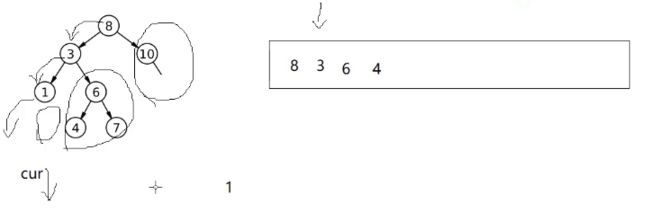
这个时候栈里取到6的时候能不能访问6?
可以访问,但这是你的感知,程序识别不出来
因为右为空才取栈里的元素访问,
这里会有两次取到6,第一次是它的右树没有访问过取到6
第二次是它的右树已经访问过了取到6
怎么区分这两次呢?
定义flag会互相干扰,比如第一次取到3,3只要右不为空就置为true
再取到6不为空
所以你会分不清是3的flag还是6的flag
因为这里可能有连续多个结点右不为空
怎样识别6的右树被访问过了还是没有访问过?
写代码
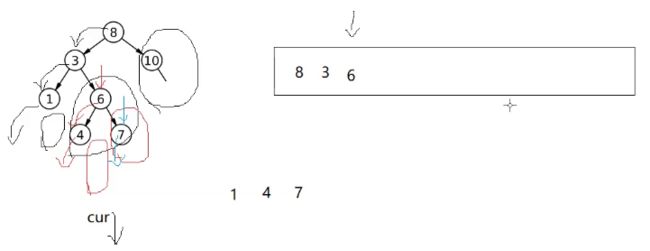
现在这样肯定死循环了
因为第一次到6第二次到6区分不开,每次6都不为空
一直67死循环
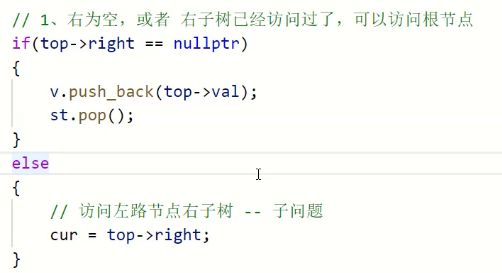
怎么识别呢
后序,左子树右子树根,在访问根的上一个结点是谁?
要访问6,6的是一个访问的结点是7
也就是右树的根。
有两种情况:

太巧了