【C语言数据结构】kruskal算法,求最小生成树,代码简单实现,深度解析
目录
kruskal算法思路
编辑
代码实现
编写 边结构体
编写push函数
编写kruskal函数
完整代码
结尾
kruskal算法思路
代码实现
这个代码是在图的邻接矩阵(无项、有权)的代码的基础上,添加了kruskal最小生成树的函数,并且修改测试用例和主函数代码,图的邻接矩阵(无项、有权)的代码具体请查看 【C语言\数据结构】图之邻接矩阵(无向、有权)代码简单实现,这里就不过多赘述。
编写 边结构体
typedef struct {
int start;
int end;
int weight;
}edge;创建一个边结构体,用来表示一条边的起点和终点以及权值。
编写push函数
void push(edge temp,edge edges[],int edgesCount){
int index=edgesCount-1;
while(index>=0&&edges[index].weight>temp.weight){
edges[index+1]=edges[index];
index--;
}
edges[index+1]=temp;
}push函数中,第一个参数是边结构体类型的变量temp,temp表示一条边。第二个参数是边结构体数组edges,按照边的权值升序存储edge数据类型,用来模拟优先队列。第三个参数是edgesCount,表示edges数组的元素个数,用来对edges数组进行尾插操作。
edges数组按照边的权值,升序存储数据,每一次添加数据,把数据插入到指定位置,从最后一个元素开始遍历,如果该权值大于插入元素的权值,就往后赋值,挪一个位置,依次循环。循环结束标志有两个,第一个是遍历完所有元素,第二个是找到了指定的位置。最后把temp插入指定位置即可。
相同结构体数据类型变量直接赋值,表示把各成员变量数据依次赋值。
编写kruskal函数
void kruskal(graph g) {
int sum = 0;
edge temp;
edge edges[MAX];
edge edgesGather[MAX];
int edgesGatherCount = 0;
int edgesCount = 0;
for (int i = 1; i <= g.vexnum; i++) {
for (int j = i; j <= g.vexnum; j++) {
if (g.arcs[i][j] != 0 && g.arcs[i][j] < INFINITY) {
temp.start = i;
temp.end = j;
temp.weight = g.arcs[i][j];
push(temp, edges, edgesCount++);
}
}
}
int gather_maxindex = 0;
int gather[MAX] = {0};
for (int i = 0; i < edgesCount; i++) {
int start, end, weight;
start = edges[i].start;
end = edges[i].end;
weight = edges[i].weight;
if ((gather[start] == gather[end] && gather[start] == 0) || gather[start] != gather[end]) {
if ((gather[start] == gather[end] && gather[start] == 0)) {
gather[start] = ++gather_maxindex;
gather[end] = gather_maxindex;
} else if (gather[start] != 0 && gather[end] != 0) {
int gathernum = gather[end];
for (int j = 1; j <= g.vexnum; j++) {
if (gather[j] == gathernum) {
gather[j] = gather[start];
}
}
} else if (gather[end] != 0) {
gather[start] = gather[end];
} else if (gather[start] != 0) {
gather[end] = gather[start];
}
edgesGather[edgesGatherCount].start = start;
edgesGather[edgesGatherCount].end = end;
edgesGatherCount++;
sum += weight;
}
}
printf("最小生成树权值和:\n%d\n", sum);
printf("最小生成树的结构:\n");
for (int i = 0; i < edgesGatherCount; i++) {
printf("%d---%d\n", edgesGather[i].start, edgesGather[i].end);
}
} int sum=0;
edge temp;
edge edges[MAX];
edge edgesGather[MAX];
int edgesGatherCount=0;
int edgesCount=0;定义sum变量,用来存储最小生成树的权值和。
定义temp变量,用来表示一条边。
定义edges数组变量,用来按照权值大小升序存储边。
定义edgesGather数组,用来存储最小生成树的边信息。
定义edgesGatherCount变量,用来存储edgesGather数组的元素个数。
定义edgesCount变量,用来存储edges数组的元素个数。
for(int i=1;i<=g.vexnum;i++){
for(int j=i;j<=g.vexnum;j++){
if(g.arcs[i][j]!=0&&g.arcs[i][j]遍历每一条边,如果这条边存在,就把起点,终点,权值这三个信息修正到temp边中,把temp边添加到edges数组中。
这样一来,edges数组就按照权值升序,存储了每一条边的信息。
int gather_maxindex=0;
int gather[MAX]={0};定义gather数组,用来表示每一个顶点所在的集合,例如gather[i]=x,表示顶点i在集合x中。
定义garher_maxindex变量,用来表示集合的最大表示数,当需要新表示一个集合,只需要把这个数+1之后使用就可以了。
for (int i = 0; i < edgesCount; i++) {
int start, end, weight;
start = edges[i].start;
end = edges[i].end;
weight = edges[i].weight;
if ((gather[start] == gather[end] && gather[start] == 0) || gather[start] != gather[end]) {
if ((gather[start] == gather[end] && gather[start] == 0)) {
gather[start] = ++gather_maxindex;
gather[end] = gather_maxindex;
} else if (gather[start] != 0 && gather[end] != 0) {
int gathernum = gather[end];
for (int j = 1; j <= g.vexnum; j++) {
if (gather[j] == gathernum) {
gather[j] = gather[start];
}
}
} else if (gather[end] != 0) {
gather[start] = gather[end];
} else if (gather[start] != 0) {
gather[end] = gather[start];
}
edgesGather[edgesGatherCount].start = start;
edgesGather[edgesGatherCount].end = end;
edgesGatherCount++;
sum += weight;
}
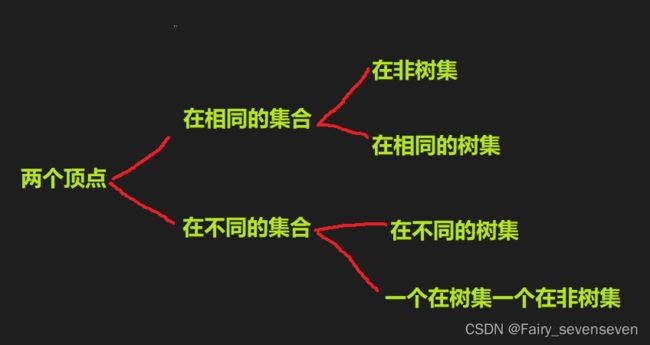
}首先必须理清一条边中,两个顶点之间的关系,要么这两个顶点在同一集合,要么这两个点在不同的集合,在相同的集合,又分为这个集合是树集或者这个集合是非树集。
在不同的集合中,分为在不同的树集中,或者一个在树集一个在非树集。
这是所有情况的分类,对于一条边我们接不接受,取决于把这条边加入到树结构中,会不会导致原本的结构不再是树,所以这条边的两个顶点不能是在相同的数集中。
if ((gather[start] == gather[end] && gather[start] == 0) || gather[start] != gather[end]) {
如果两个顶点在不同的集合,或者他们在相同非树集中,就表示接受这条边。
if ((gather[start] == gather[end] && gather[start] == 0)) {
gather[start] = ++gather_maxindex;
gather[end] = gather_maxindex;
如果他们都在非树集中,就必须创建一个新的集合,表示把他们添加到树结构中,修改这两个顶点gather的值,这个值的取值只要是之前没有使用过的值就可以了,因为这个值只是表示一个集合,等于这个值的所有顶点都在一个集合,等于0是非树集,不等于0是树集,所以为了保证这个值没有被使用过,取使用过的值的最大值,先++再使用它。
} else if (gather[start] != 0 && gather[end] != 0) {
int gathernum = gather[end];
for (int j = 1; j <= g.vexnum; j++) {
if (gather[j] == gathernum) {
gather[j] = gather[start];
}
}
如果这两个顶点在不同的树集中,只需要把其中一个树集中所有元素的gather值,写成另一个树集的gather表示值就可以了,这样一来两个顶点的gather值就相同了,相同表示在同一集合。遍历end所有顶点的gather值,如果等于end顶点的gather就维护成start的gather值。
} else if (gather[end] != 0) {
gather[start] = gather[end];
} else if (gather[start] != 0) {
gather[end] = gather[start];
}
如果他们是一个在树集另一个在非树集,只需要把非树集添加到指定树集就可以了。
edgesGather[edgesGatherCount].start = start;
edgesGather[edgesGatherCount].end = end;
edgesGatherCount++;
sum += weight;
最后尾插这条边,把该边的权值添加到sum的值中,因为只要在树集中,最后都会变成一颗树,而不是两颗,或者其他,所以每接受一条边就添加到sum中。
printf("最小生成树权值和:\n%d\n",sum);
printf("最小生成树的结构:\n");
for(int i=0;i最后输出最小生成树的权值和,并且输出最小生成的结构。
完整代码
#include
#include
#include
#include
#define MAX 100
#define INFINITY 9999
enum graphType {DG, UG, DN, UN}; //图的类型定义:有向图,无向图,有向网,无项网
typedef char vertexType;
typedef struct {
vertexType vexs[MAX];
int arcs[MAX][MAX];
int vexnum, arcnum;
graphType kind;
} graph;
typedef struct {
int start;
int end;
int weight;
} edge;
void initGraph(graph &g) {
g.kind = UN;
printf("输入顶点数和边数:\n");
scanf("%d%d", &g.vexnum, &g.arcnum);
for (int i = 1; i <= g.vexnum; i++) {
g.vexs[i] = i;
}
for (int i = 1; i <= g.vexnum; i++) {
for (int j = 1; j <= g.vexnum; j++) {
if (i == j) g.arcs[i][j] = 0;
else g.arcs[i][j] = INFINITY;
}
}
}
void createGraph(graph &g) {
int start_index, end_index, weight;
printf("输入每条边的起点终点下标和边的权重:\n");
for (int i = 1; i <= g.arcnum; i++) {
scanf("%d%d%d", &start_index, &end_index, &weight);
g.arcs[start_index][end_index] = weight;
g.arcs[end_index][start_index] = weight;
}
}
void showGraph(graph &g) {
printf("邻接矩阵:\n");
for (int i = 1; i <= g.vexnum; i++) {
for (int j = 1; j <= g.vexnum; j++) {
printf("%d ", g.arcs[i][j]);
}
printf("\n");
}
}
void push(edge temp, edge edges[], int edgesCount) {
int index = edgesCount - 1;
while (index >= 0 && edges[index].weight > temp.weight) {
edges[index + 1] = edges[index];
index--;
}
edges[index + 1] = temp;
}
void kruskal(graph g) {
int sum = 0;
edge temp;
edge edges[MAX];
edge edgesGather[MAX];
int edgesGatherCount = 0;
int edgesCount = 0;
for (int i = 1; i <= g.vexnum; i++) {
for (int j = i; j <= g.vexnum; j++) {
if (g.arcs[i][j] != 0 && g.arcs[i][j] < INFINITY) {
temp.start = i;
temp.end = j;
temp.weight = g.arcs[i][j];
push(temp, edges, edgesCount++);
}
}
}
int gather_maxindex = 0;
int gather[MAX] = {0};
for (int i = 0; i < edgesCount; i++) {
int start, end, weight;
start = edges[i].start;
end = edges[i].end;
weight = edges[i].weight;
if ((gather[start] == gather[end] && gather[start] == 0) || gather[start] != gather[end]) {
if ((gather[start] == gather[end] && gather[start] == 0)) {
gather[start] = ++gather_maxindex;
gather[end] = gather_maxindex;
} else if (gather[start] != 0 && gather[end] != 0) {
int gathernum = gather[end];
for (int j = 1; j <= g.vexnum; j++) {
if (gather[j] == gathernum) {
gather[j] = gather[start];
}
}
} else if (gather[end] != 0) {
gather[start] = gather[end];
} else if (gather[start] != 0) {
gather[end] = gather[start];
}
edgesGather[edgesGatherCount].start = start;
edgesGather[edgesGatherCount].end = end;
edgesGatherCount++;
sum += weight;
}
}
printf("最小生成树权值和:\n%d\n", sum);
printf("最小生成树的结构:\n");
for (int i = 0; i < edgesGatherCount; i++) {
printf("%d---%d\n", edgesGather[i].start, edgesGather[i].end);
}
}
int main() {
graph g;
initGraph(g);
createGraph(g);
showGraph(g);
kruskal(g);
}
/*测试用例:
5 8
1 2 1
1 5 4
1 3 3
2 4 2
4 5 4
3 4 1
2 3 2
3 5 1
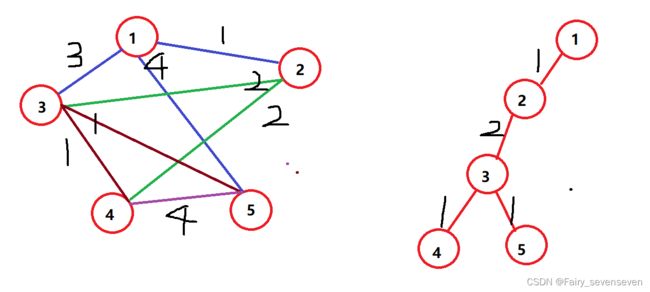
*/ 代码运行截图:
可以验证,创建出来的最小生成树长度和连接情况是没有问题的。
结尾
我们今天学习了kruskal算法求最小生成树。首先我们引入了集合的概念,gather[i]=x表示顶点i在集合x中,依次遍历图中所有的边,依次加入到edges数组中,根据权值 进行升序排序,模拟优先队列。
依次遍历edges也就是权值最小的边,然后判断这条边的两个顶点是否在同一树集,如果不在同一树集,连接这条边构成的还是树,这条边就可以接受,依次循环,一直到edges数组变量结束。不要忘记每次添加到树集的边要存储到数组中,遍历数组就可以还原最小生成树的结构哦。
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!