【一】【C语言\动态规划】动态规划——第 N 个泰波那契数、三步问题,使用最小花费爬楼梯 ,三道题目深度解析
动态规划
动态规划是一种思想,利用动态规划的思想可以很方便的解决某些题目。
动态规划简单来说,就是建立一个dp表,dp表上每个位置对应一个状态,通过前后位置的状态推导出自己的状态,这个所谓的状态定义通常是依据经验和题目要求来定义。
我们需要怎么把动态规划的思想在题目中运用?
按照以下步骤,
-
状态表示:
-
状态转移方程:
-
初始化:
-
填表顺序:
-
返回值:
如果看不懂没有关系,我们将通过四道例题讲解动态规划。
注意,点击标题可以到leetcode原地址。
第 N 个泰波那契数
首先我们先把步骤抄过来。
-
状态表示:
-
状态转移方程:
-
初始化:
-
填表顺序:
-
返回值:
状态表示
首先,题目给我们一个n值,要求我们返回第n个泰波那契数的值。
那我们可以定义状态为:dp[i] 表示第i个泰波那契数的值。
我们创建一个dp表,也就是dp数组,dp数组每个位置上表示一种状态,而这个状态的含义由题目意思+经验来得到,在这道题目我们就定义为,dp[i] 表示第i个泰波那契数的值。
状态转移方程
我们创建dp表的目的是使dp表上所有位置都填上我们需要的值,而填表的过程就是通过前一个状态推出后一个状态,或者由后一个状态推出前一个状态,而这个的推导过程就由转移方程得到。
通过题目意思,我们可以得到,
dp[i]=dp[i-1]+dp[i-2]+dp[i-3]
我们想要得到dp表中第i个位置的状态,我们可以由前三个状态相加得出。
这种由身边的状态推导出自己状态的值的方式就是动态规划。
初始化
我们先创建一个dp数组,也就是dp表
dp表中,dp[i] 表示第i个泰波那契数的值。
然后我们的目的是需要把dp表中的位置填满。
而填表的过程需要利用前面三个状态,但是对于数组中前三个位置的状态,我们找不到完整的前三个状态,我们通过状态转移方程推导的时候会造成越界的情况,所以为了防止越界,我们需要对dp表进行初始化。
很明显,只需要对前三个值进行初始化就可以了。
即:dp[0]=0,dp[1]=1,dp[2]=1;
填表顺序
很明显是从左向右,即从i=3开始往后依次填表,一直填到n。
返回值
题目给我们一个n的值,要求我们返回第n个泰波那契值,根据状态表示,dp[i] 表示第i个泰波那契数的值,所以我们需要放回dp[n]。
代码实现
int tribonacci(int n){
//状态表示
//状态转移方程
//初始化
//填表
//返回值
//dp[i]第i个泰波那契数 Tn 的值
//dp[i]=dp[i-1]+dp[i-2]+dp[i-3]
//dp[0]=0,dp[1]=dp[2]=1
//...
//dp[n]
if(n==0) return 0;
if(n==1) return 1;
if(n==2) return 1;
int dp[n+1];
dp[0]=0;
dp[1]=1;
dp[2]=1;
for(int i=3;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2]+dp[i-3];
}
return dp[n];
}创建dp表
首先我们需要创建一个dp表,对dp表中状态的定义是,dp[i] 表示第i个泰波那契数 Tn 的值。我们需要得到第n个泰波那契数的值,所以dp空间需要n+1。
初始化
然后我们为了访问数组时不越界,需要对前三个状态进行初始化。
即:dp[0]=0; dp[1]=1; dp[2]=1;
填表
我们从第三个状态开始填表,一直到第n个状态。
每一个状态的值都是前三个状态的值的和。
返回值
返回dp[n],第n个状态,dp[i] 表示第i个泰波那契数 Tn 的值,也就是第n个泰波那契数的值。
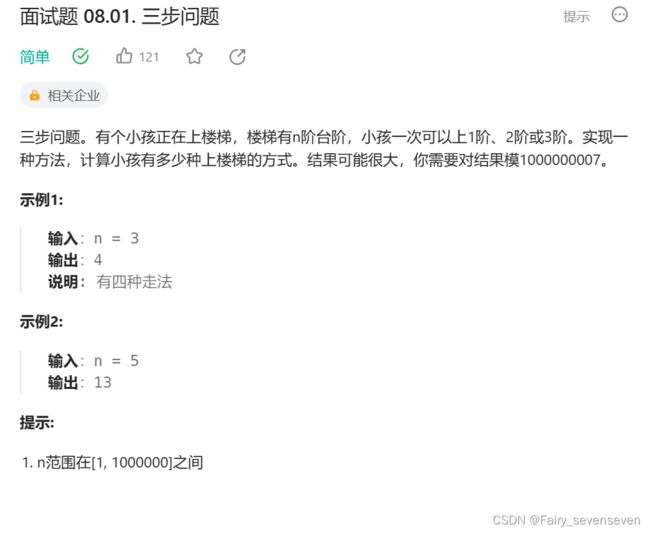
面试题 08.01. 三步问题
题目分析:
首先我们先把步骤抄过来。
-
状态表示:
-
状态转移方程:
-
初始化:
-
填表顺序:
-
返回值:
状态表示
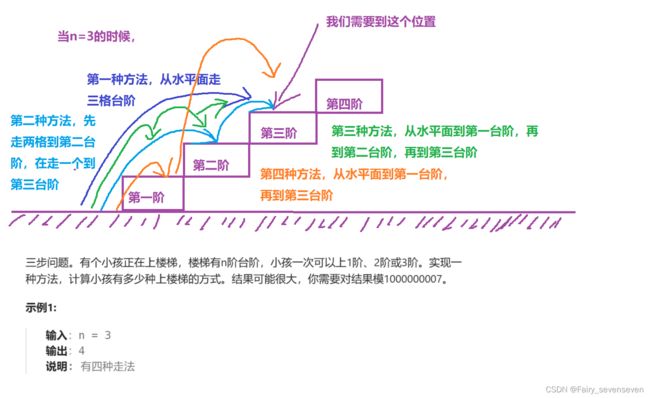
题目给我们一个n的值,要求我们返回小孩从水平面到第n阶台阶的方法数。
因此我们可以定义状态,dp[i]表示从水平面到达第i阶台阶的方法数。
状态转移方程
我们想一想dp[i]能不能从其他状态的值推导出来?
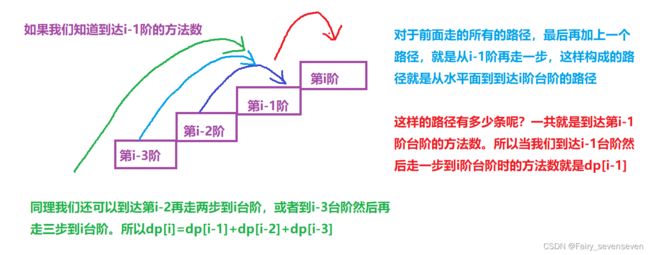
很明显,我们想要到达第i阶台阶,要么先到达第i-1阶台阶然后走一步,要么先到达第i-2阶台阶然后走两步,要么先到达第i-3阶台阶然后走三步。
那么状态转移方程我们就可以定义为,
dp[i]=d[i-1]+dp[i-2]+dp[i-3]
意思是,如果我们知道dp[i-1]的值,不管前面是怎么走的,只要再走一步就算到达第i阶台阶,对于dp[i-1]表示从水平面到达第i-1的方法数,这些方法、路径,再走一步,就算是到达第i阶台阶的方法。
同理,我们加上dp[i-2],dp[i-3]。
初始化
为了在填表过程对dp数组访问时不越界,我们需要初始化dp[1],dp[2],d[3]。
dp[i]表示从水平面到达第i阶台阶的方法数。
即:
dp[1]=1,dp[2]=2,dp[3]=4。
填表顺序
从左到右
返回值
根据状态的定义:dp[i]表示从水平面到达第i阶台阶的方法数。
返回dp[n]。
代码实现
int waysToStep(int n){
//状态表示 dp[i] 从0层到第i阶台阶的上楼梯方法数
//状态转移方程 dp[i]=dp[i-1]+dp[i-2]+dp[i-2]
//初始化
//填表
//返回值
const int MOD=1e9+7;
if(n==1) return 1;
if(n==2) return 2;
if(n==3) return 4;
int dp[n+1];
dp[1]=1;
dp[2]=2;
dp[3]=4;
for(int i=4;i<=n;i++){
dp[i]=((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;
}
return dp[n];
}
创建dp表
根据状态定义,dp[i]表示从水平面到达第i阶台阶的方法数,以及我们需要返回到达第n台阶的方法数,所以需要表示dp[n],需要至少n+1大小的数组。
初始化
为了在对dp数组访问的时候不越界,我们需要对dp[1],dp[2],dp[3] 进行初始化。
即:dp[1]=1; dp[2]=2; dp[3]=4;
填表
根据状态转移方程,dp[i]=d[i-1]+dp[i-2]+dp[i-3],直接抄上去,但是哦我们需要注意一些细节,题目中说我们得到的数值可能很大,需要对1e9+7进行求余,所以对于每一个dp值相加之后,需要求一次余。对需要求余的数我们通常定义为MOD。
返回值
返回dp[n]。
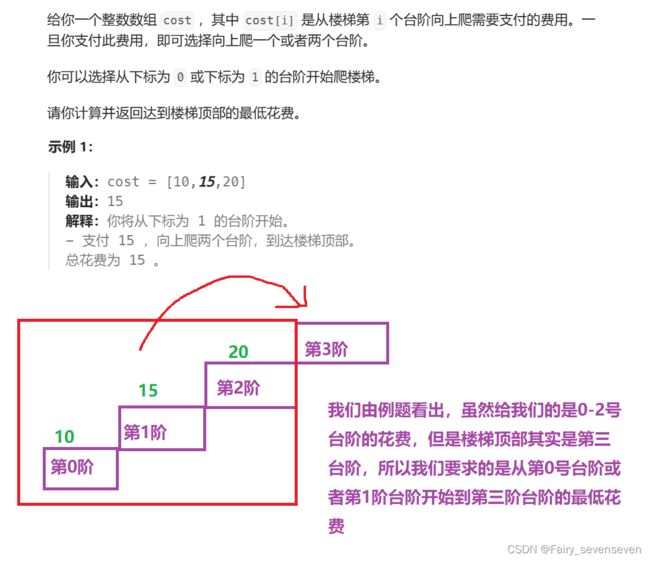
746. 使用最小花费爬楼梯
题目分析:
状态表示
根据题意我们可以定义,dp[i]表示从0或者1台阶开始,到达第i阶台阶的最低花费,
示例1表示我们要求dp[3]的值。
状态转移方程
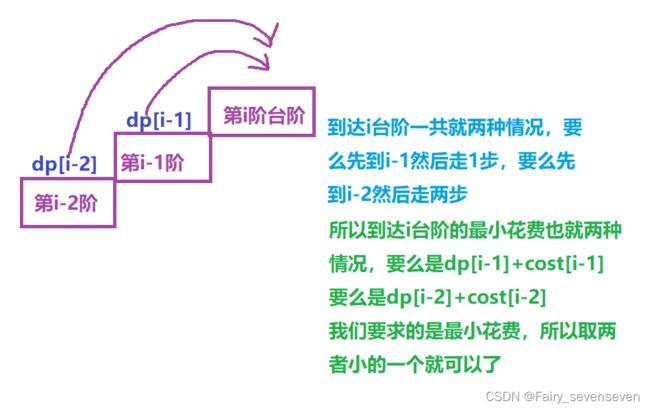
假如我们需要得到dp[i]的值,也就是到达第i阶台阶的最低花费,首先我们分析到达第i阶台阶的情况,如果我们要到达第i阶台阶,我们有两种情况,第一种就是我们到达了i-1阶台阶,然后走1步到达i阶台阶,或者我们先到达了i-2阶台阶,然后我们走2步到达i阶台阶。
而到达i阶台阶的最低花费就是,这两种方式、路径其中花费小的那个花费。
也就是到达i-1台阶的最低花费加上第i-1的花费,与到达i-2台阶的最低花费加上第i-2的花费比较,谁小,谁就是到i阶台阶的最小花费。
即:dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
初始化
根据状态转移方程,我们得到i位置的状态需要i-1和i-2的状态推导出来,所以我们为了在访问dp数组时不越界,需要对dp[0],dp[1]初始化,
即:dp[0]=0,di[1]=0;
因为我们可以选择0或者1位置出发,所以两者都不需要花费就可以到达。
填表顺序
从左到右
返回值
给我们的是cost数组,我们需要到达的楼顶是cost最后一个元素下标值+1,也就是cost的雅元素个数,所以我们返回dp[size.cost]就可以了。
代码实现
int minCostClimbingStairs(int* cost, int n) {
//状态表示 dp[i] 从最开始出发,到达第i个台阶的最低花费
//状态转移方程 dp[i]= min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
//初始化
//填表
//返回值
//细节:边界
if(n==0) return 0;
if(n==1) return 0;
int dp[n+1];
dp[0]=0;
dp[1]=0;
for(int i=2;i<=n;i++){
dp[i]=fmin(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
}
return dp[n];
}创建dp表
根据状态表示,dp[i]表示从0或者1台阶开始,到达第i阶台阶的最低花费,以及题目要求,我们需要返回 到 ”cost数组大小“ 阶台阶的最低花费
所以我们需要表示dp[n],所以dp数组大小需要n+1。
初始化
为了在填表的过程中,对dp表的访问不越界,我们需要初始化前两个状态的值,即dp[0]=0,dp[1]=0。我们可以选择从0或者1台阶开始,所以他们的花费是0。
填表
for(int i=2;i<=n;i++){
dp[i]=fmin(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
}从第二个状态开始填,一直到第n个状态,直接把状态转移方程抄过来。
返回值
返回dp[n]
结尾
今天我们学习了动态规划的思想,对于某些题目,根据题目+经验,我们可以定义出状态表示,然后根据前面的状态表示出自己的状态或者根据后面的状态表示出自己的状态,这就叫动态规划,而从前面状态推导出自己的状态,需要根据状态转移方程,状态转移方程由对题目的分析得到,然后我们对于dp表的访问不能越界,所以我们需要对dp表进行初始化,最后是分析填表顺序和返回值。
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!