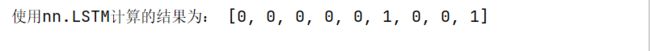【23-24 秋学期】NNDL 作业11 LSTM

目录

习题6-4 推导LSTM网络中参数的梯度， 并分析其避免梯度消失的效果

习题6-3P 编程实现下图LSTM运行过程

（一）numpy实现 

（二）使用nn.LSTMCell实现

（三） 使用nn.LSTM实现

总结

（一）推荐

 （二）关于LSTM的有关推导

（三）有关LSTM的代码

---

参考【【23-24 秋学期】NNDL 作业11 LSTM-CSDN博客

习题6-4 推导LSTM网络中参数的梯度， 并分析其避免梯度消失的效果

在我的上一篇博客【【23-24 秋学期】NNDL 作业10 BPTT-CSDN博客】中：

可以看到对于梯度爆炸/消失的推导，其中关键部分就在于递归梯度：这一部分。

对于求解LSTM网络中的梯度消失也同理-----关键部分也就是内部状态递归梯度 的变化。

先求解一下这个 如下：

 然后假设损失为E，与上上图求解类似，如下：

参考【LSTM 如何避免梯度消失问题 - 知乎 (zhihu.com)】 这个作者的那个参考网址我点不开，看不了更原始的。

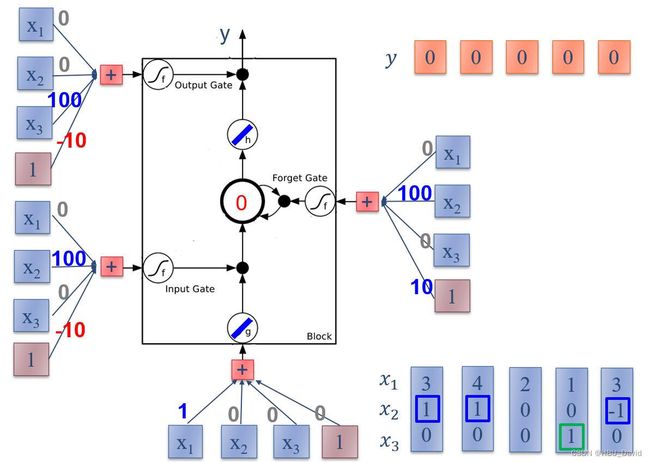
习题6-3P 编程实现下图LSTM运行过程

（一）numpy实现 

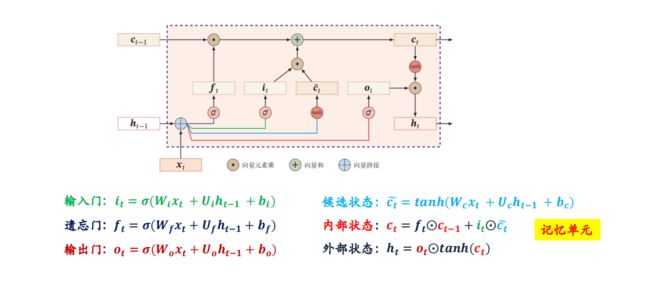
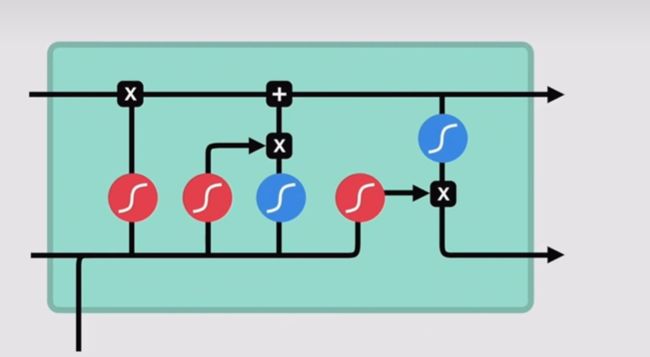
简单分析一下，这个LSTM的运行过程：主要包括三个门，加一个输入，中间层，以及输出层。

输入门的作用是：是否要保存输入结果

遗忘门的作用是：是否要把得到的输入结果存到延迟器中去，也就是隐藏层中

输出门的作用是是否把隐藏层的结果输出

需要强调的是，1）输入这一块也是有一个激活的，但是没使用，隐藏层向输出也是。和，所以我在实现的时候就没有写这一块激活。

2）对于中间隐藏层而言，他就是一个延迟器，所以当遗忘门为1时，它就会累加输入；为0时会清零。

3）对于激活函数sigmoid，它最后的结果类似一个概率，是处于【0，1】之间的一个数，但是由于这道题中最开始的要求，所以我在实现激活函数时，使用np.round()，把结果>0.5作为1输出，结果<0.5的作为0输出，这是特殊情况。

代码如下：

import numpy as np

# x=[x1,x2,x3,bias]
x = [[1, 0, 0, 1], [3, 1, 0, 1], [2, 0, 0, 1], [4, 1, 0, 1], [2, 0, 0, 1], [1, 0, 1, 1], [3, -1, 0, 1], [6, 1, 0, 1], [1, 0, 1, 1]]
# input
input_w = [1, 0, 0, 0]
# 输入门
inputGate_w = [0, 100, 0, -10]
# 遗忘门
forgetGate_w = [0, 100, 0, 10]
# 输出门
outputGate_w = [0, 0, 100, -10]

# 激活
def sigmoid(x):
    return np.round(1 / (1 + np.exp(-x)))

# 延时器
hidden = []
y = []
temp = 0.0

for input in x:
    hidden.append(temp)
    # 输入与与对应权值相乘再相加
    temp_input = np.sum(np.multiply(input, input_w))
    # 输入门【得 1 or 得 0】
    temp_inputGate = sigmoid(np.sum(np.multiply(input, inputGate_w)))
    # 遗忘门
    temp_forgetGate = sigmoid(np.sum(np.multiply(input, forgetGate_w)))
    # 延时器
    temp = temp_input * temp_inputGate + temp * temp_forgetGate
    # 输出门
    temp_outputGate = sigmoid(np.sum(np.multiply(input, outputGate_w)))
    # 输出
    temp_y = temp * temp_outputGate
    y.append(temp_y)

print("延时器：", hidden)
print("输出y： ", y)

得到的结果为：

我就止步到此了。

参考了我们班学霸博客【指路：DL Homework 11-CSDN博客

 发现他对于输入和输出的激活函数有研究，在他博客里提到：

课程指路【 李宏毅手撕LSTM_哔哩哔哩_bilibili

我自己的理解就是：在LSTM的模型中，规定了输入输出状态的激活函数 和是tanh函数，与我们实现的代码有一些区别。并且nn.LSTM的内部激活函数，没办法修改，所以仿照学霸的，写了一个检验版【也就是加上tanh版本的】

代码如下：

import numpy as np

# x=[x1,x2,x3,bias]
x = [[1, 0, 0, 1], [3, 1, 0, 1], [2, 0, 0, 1], [4, 1, 0, 1], [2, 0, 0, 1], [1, 0, 1, 1], [3, -1, 0, 1], [6, 1, 0, 1], [1, 0, 1, 1]]
# input
input_w = [1, 0, 0, 0]
# 输入门
inputGate_w = [0, 100, 0, -10]
# 遗忘门
forgetGate_w = [0, 100, 0, 10]
# 输出门
outputGate_w = [0, 0, 100, -10]

# 激活
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# 延时器
hidden = []
y = []
temp = 0

for input in x:
    hidden.append(temp)
    # 输入与与对应权值相乘再相加
    #加tanh激活
    temp_input = np.tanh(np.sum(np.multiply(input, input_w)))
    # 输入门【得 1 or 得 0】
    temp_inputGate = sigmoid(np.sum(np.multiply(input, inputGate_w)))
    # 遗忘门
    temp_forgetGate = sigmoid(np.sum(np.multiply(input, forgetGate_w)))
    # 延时器
    #加tanh激活
    temp = np.tanh(temp_input * temp_inputGate + temp * temp_forgetGate)
    # 输出门
    temp_outputGate = sigmoid(np.sum(np.multiply(input, outputGate_w)))
    # 输出
    temp_y = temp * temp_outputGate
    y.append(temp_y)

rounded_hidden = [round(x) for x in hidden]
print("检验版延时器：", rounded_hidden)

rounded_y = [round(x) for x in y]
print("检验版输出y： ", rounded_y)

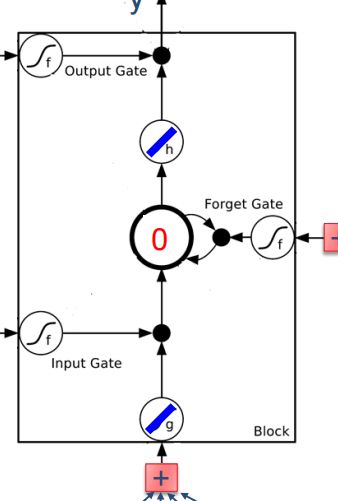
其中按照下图：

将tanh函数加到输入以及输出之前。 

得到输出为：

 

（二）使用nn.LSTMCell实现

参考【PyTorch - torch.nn.LSTMCell (runebook.dev)】【汉语版，感觉比网页英转汉好用多了】

 可知我们实现的各个值为：

input_size=4

hidden_size=1

偏差bias=False

细胞状态cx=(1,hidden_size)#因为每次运算都是输入的一个批次

同理隐藏状态=(1,hidden_size)

import torch
import torch.nn as nn
#x 维度需要变换，因为LSTMcell接收的是(time_steps,batch_size,input_size)
x = torch.tensor([[1, 0, 0, 1],[3, 1, 0, 1],[2, 0, 0, 1], [4, 1, 0, 1],[2, 0, 0, 1],[1, 0, 1, 1], [3, -1, 0, 1],[6, 1, 0, 1],[1, 0, 1, 1]], dtype=torch.float)
x = x.unsqueeze(1)
#权重
input_w = [1, 0, 0, 0]# input
inputGate_w = [0, 100, 0, -10]# 输入门
forgetGate_w = [0, 100, 0, 10]# 遗忘门
outputGate_w = [0, 0, 100, -10]# 输出门
#输入形状每次一组，一组是【x1,x2,x3,bias】
input_size=4
hidden_size=1
#定义LSTM
cell=nn.LSTMCell(input_size=input_size,hidden_size=hidden_size,bias=False)
#输入隐藏权重，形状为 (4*hidden_size, input_size)
cell.weight_ih.data = torch.tensor([forgetGate_w, inputGate_w, input_w, outputGate_w], dtype=torch.float)
#隐藏权重，形状为 (4*hidden_size, hidden_size)
cell.weight_hh.data=torch.zeros([4*hidden_size,hidden_size])

#hx 和 cx 的初始值都需要初始化为全零张量，表示没有历史信息。
hx=torch.zeros(1,hidden_size)#hx 表示隐藏状态
cx=torch.zeros(1,hidden_size)#cx 表示细胞状态
outputs=[]
for i in range(len(x)):
    #这里没有区分c0,n0和c1,h1：因为使用了递归，也就是这次的输出是下次的输入
    hx, cx = cell(x[i], (hx, cx))
    outputs.append(hx.detach().numpy()[0][0])
#约数
outputs_rounded = [round(x) for x in outputs]
print("使用nn.LSTMCell的输出为：",outputs_rounded)

得到输出为：

（三） 使用nn.LSTM实现

参考【PyTorch - torch.nn.LSTM (runebook.dev)

 与Cell不同的是隐藏状态和细胞状态，其中多加了一个有关序列长度的维度。

代码如下：

import torch
import torch.nn as nn

#x 维度需要变换，因为LSTMcell接收的是(time_steps,batch_size,input_size)
x = torch.tensor([[1, 0, 0, 1],[3, 1, 0, 1],[2, 0, 0, 1], [4, 1, 0, 1],[2, 0, 0, 1],[1, 0, 1, 1], [3, -1, 0, 1],[6, 1, 0, 1],[1, 0, 1, 1]], dtype=torch.float)
x = x.unsqueeze(1)
#权重
input_w = [1, 0, 0, 0]# input
inputGate_w = [0, 100, 0, -10]# 输入门
forgetGate_w = [0, 100, 0, 10]# 遗忘门
outputGate_w = [0, 0, 100, -10]# 输出门
#输入形状每次一组，一组是【x1,x2,x3,bias】
input_size=4
hidden_size=1
#定义LSTM模型
lstm=nn.LSTM(input_size=input_size,hidden_size=hidden_size,bias=False)
#设置LSTM的权重矩阵
#输入隐藏权重，形状为 (4*hidden_size, input_size)
lstm.weight_ih_l0.data = torch.tensor([forgetGate_w, inputGate_w, input_w, outputGate_w], dtype=torch.float)
#隐藏权重，形状为 (4*hidden_size, hidden_size)
lstm.weight_hh_l0.data=torch.zeros([4*hidden_size,hidden_size])
# 初始化隐藏状态和记忆状态
hx = torch.zeros(1, 1, hidden_size)
cx = torch.zeros(1, 1, hidden_size)

# 前向传播
outputs, (hx, cx) = lstm(x, (hx, cx))
#所有维度值为 1 的维度都删除
outputs = outputs.squeeze().tolist()

#约数
outputs_rounded = [round(x) for x in outputs]
print("使用nn.LSTM计算的结果为：",outputs_rounded)

结果为：

总结

（一）推荐

首先是给大家推荐一下课程，有老师上课讲的下边这种动图：

然后我在推导有关Ct的递归梯度时，也是参考了这个视频，博主【苏坡爱豆的笑容】讲的很清楚！！！

 【清晰图解LSTM、BPTT、RNN的梯度消失问题】

 还有上个博客听的那个视频【也有关于LSTM推导的内容】：【循环神经网络讲解｜随时间反向传播推导(BPTT)｜RNN梯度爆炸和梯度消失的原因｜LSTM及GRU(解决RNN中的梯度爆炸和梯度消失)-跟李沐老师动手学深度学习】

都非常nice！

还有一篇知乎的文章解释有关避免梯度消失的也特别好！地址如下：LSTM 如何避免梯度消失问题 - 知乎 (zhihu.com)

然后在看了博客：DL Homework 11-CSDN博客 后，感觉可以推荐一下关于pytorch的汉化版【我读英语头昏脑胀，适合不喜欢学英语的同学，指路：PyTorch 1.8 简体中文 (runebook.dev)】

 （二）关于LSTM的有关推导

这个与上一个作业关联挺大的，很类似，都是在递归推导。可以发现，这个模型中减少梯度消失现象的很重要的一个点就是对于门控单元【遗忘门】的把控。可以及时的缓解梯度消失。

（三）有关LSTM的代码

第一个numpy能写出来，但是关于输出输出位置的激活函数没有多想，参考了学霸的代码后发现他研究了关于这一部分，学到了很多---也就是有激活tanh函数只是写的例子里边把激活函数换成了一个输入几输出几的这样一个激活而已【我自己觉得跟去掉了激活没什么区别】

在pytorch默认的模型里是tanh激活函数。

自己在网上搜关于使用LSTM相关模型时写不出来，学会使用现成的工具是一种能力，然后这个LSTM模型好像没有手写过，我还是不太会内部结构【下几个实验有这个内容，我好好+认真写】