【AI】数学基础——数理统计（概念&参数估计）

概率论

数理统计（假设检验&数据处理）

数理统计的任务是根据可观察的样本反过来推断总体的性质

推断的工具是统计量，统计量是样本的函数，是个随机变量

参数估计通过随机抽取的样本来估计总体分布的未知参数，包括点估计和区间估计

假设检验通过随机抽取的样本来接收或拒绝关于总体的某个判断

3.6 数理统计概念与定理

3.6.1 概率论与数理统计区别

根据观察或实验得到的数据来研究随机现象，并对研究对象的客观规律做出合理的估计和判断。

• 概率论：研究对象是分布已知的随机变量，根据已知的分布来分析随机变量的特征和规律

  概率论解决的是已知彩票的要将规律，判断一注号码中奖的可能性

• 数理统计：研究对象是分布未知的随机变量，研究方法是对随机变量进行独立重复的观察，根据得到的观察结果对原始分布做出推断

  数理统计解决的是根据之前多次中奖/不中奖的号码记录以一定的精确性推测摇奖的规律

在数理统计中，可用的资源是有限的数据集——样本。观察对象所有的可能取值——总体。

• 样本通常由对总体进行多次独立的重复观测得到，并且与总体同分布

数理统计目标：根据样本推断总体数字特征

统计量 ：在统计推断中，应用的往往不是样本本身，而是被称为统计量的样本的函数，本身也是一个随机变量

样本均值：$\overline{X}=\frac{1}{n}\sum _{i=1}^n{X}_i$

样本方差：$S^2=\frac{1}{n-1}\sum _{i=1}^n(X_i-\overline{X}{)}^2$

3.6.2 基本定理

大数定理

在试验条件不变的条件下，重复多次实验，随机事件发生的频率 $\approx$ 概率

马尔科夫不等式

$P(X\ge a)\le \frac{EX}{a},X\ge 0,a>0$

证：
$$\begin{array}{rl}& X\ge a\Rightarrow \frac{X}{a}\ge 1\\ & P(X\ge a)={\int }_a^{+\infty }f(x)dx\le {\int }_a^{+\infty }\frac{x}{a}f(x)dx\\ & 由期望性质：E\left(\frac{X}{a}\right)={\int }_{-\infty }^a\frac{x}{a}f(x)dx+{\int }_a^{+\infty }\frac{x}{a}f(x)dx\stackrel{x\le 0}{}{\int }_0^a\frac{x}{a}f(x)dx+{\int }_a^{+\infty }\frac{x}{a}f(x)dx\\ & 由于{\int }_0^a\frac{x}{a}f(x)dx\ge 0\Rightarrow E\left(\frac{X}{a}\right)\ge {\int }_a^{+\infty }\frac{x}{a}f(x)dx\\ & P(X\ge a)={\int }_a^{+\infty }f(x)dx\le {\int }_a^{+\infty }\frac{x}{a}f(x)dx\le E\left(\frac{X}{a}\right)=\frac{EX}{a}\end{array}$$

切比雪夫不等式

二八定理：大部分围绕在均值附近

微笑公式：$P=\{|X-EX|\ge ϵ\}\le \frac{{\sigma }^2}{{ϵ}^2}⟺P\{|X-EX|<ϵ\}>1-\frac{{\sigma }^2}{{ϵ}^2}$

• ${\sigma }^2$ 越小，小概率事件越少
• ${\sigma }^2$ 越大，在均值附近的围绕程度越低，越分散

证明：将马尔科夫不等式中的常数 $a$ 代入为均值 $ϵ$ ，随机变量 $X$ 代入为 $|X-EX|$

eg：

$n$ 重伯努利实验，$P(A)=0.75$ ，确定实验次数 $n$ ，使 $A$ 出现的频率在 $(0.74,0.76)$ 之间的概率不超过0.9

$X\sim B(n,0.75)$ ，$EX=np=0.75n$ ，$DX=npq=\frac{3}{16}n$

在 $n$ 次实验中事件 $A$ 出现的频率为 $\frac{X}{n}$ ，$P\{0.74<\frac{X}{n}<0.76\}=\{0.74n<X<0.76n\}=\{|X-0.75n|<0.01n\}\ge 1-\frac{3n\backslash 16}{0.01n^2}\ge 0.9$

$n\ge 18750$

中心极限定理

任何一个总体的平均值都会围绕在总体的平均值附近

3.6.3 统计推断的基本问题

参数估计：对象是总体的某个参数

假设检验：对象是总体的某个论断，即关于总体的假设

3.7 参数估计

3.7.1 频率派

D : d a t a = ( X 1 , X 2 , ⋯   , X n ) T = ( x 11 x 12 ⋯ x 1 p x 21 x 22 ⋯ x 2 p ⋮ ⋮ ⋱ ⋮ x n 1 x n 2 ⋯ x n p ) ⏞ p 个维度 D:data=(X_1,X_2,\cdots,X_n)^T=\overbrace{\left(\begin{matrix}x_{11}&x_{12}&\cdots&x_{1p}\\x_{21}&x_{22}&\cdots&x_{2p}\\\vdots&\vdots&\ddots&\vdots\\x_{n1}&x_{n2}&\cdots&x_{np}\end{matrix}\right)}^{p个维度} D:data=(X1​,X2​,⋯,Xn​)T= ​x11​x21​⋮xn1​​x12​x22​⋮xn2​​⋯⋯⋱⋯​x1p​x2p​⋮xnp​​ ​ ​p个维度​ n个数据

$\theta$ 为参数，$X\sim P(X;\theta )$ ，假设 $n$ 个样本$X_i$ 整体服从一个分布

• 点估计
• 区间估计

点估计法

点估计：已知总体分布函数，但未知其中一个或多个参数时，借助总体的一个样本来估计未知参数的取值

• 核心在于构造合适的统计量 $\hat{\theta }$ ，并用这个统计量的观察值作为未知参数 $\theta$ 的近似值
• 具体方法：矩估计法和最大似然估计法

矩阵估计法

矩表示随机变量的分布特征， $k$ 阶矩定义为随机变量的 $k$ 次方的期望，即 $E(X^k)$

基本思想：用样本 $k$ 阶矩估计总体的 $k$ 阶矩

理论依据：样本矩的函数几乎处处收敛于总体矩的相应函数

• 大数定律——当样本容量足够大时，几乎每次都可以根据样本参数得到相应总体参数的近似值

极大似然估计

基本思想：认为抽样得到的这一组样本值概率较大，因而在参数估计时就需要让已有样本值出现的可能性最大

$\theta$ ：未知常量——常用极大似然估计MLE

${\theta }_{MLE}=arg\underset{\theta }{\max }L(\theta |X)=arg\underset{\theta }{\max }P(X|\theta )=arg\underset{\theta }{\max }logP(X|\theta )$

$X\stackrel{iid}{\sim }P(X|\theta )=\prod _{i=1}^{n}P(x_i|\theta )$

似然函数

给定联合样本值X是关于$\theta$ 的函数$L(\theta |X)$

• x：随机变量X的具体取值
• $\theta$：控制整体样本服从的分布

似然函数 $L(\theta |X)$ ：已知数据，求使数据出现的概率最大的分布的参数 $\theta$

似然概率 $P(X|\theta )$ ：已知样本服从的分布，即参数 $\theta$ 已知，求当 $X$ 取到样本 $X$ 时的概率

在最大似然估计中，似然函数被定义为样本观测值出现的概率，确定未知参数的准则是让似然概率最大化

离散型

$P(x_1|\theta )>P(x_2|\theta )$ ：$X$ 取 $x_1$ 的概率大

$L({\theta }_1|X)=P(X|{\theta }_1)>P(X|{\theta }_2)=L({\theta }_2|X)$

L：取到数据集 $\{X\}$ 服从${\theta }_1$ 描述的分布的概率

P：在 ${\theta }_1$ 条件下，取到 $\{X\}$ 的概率

连续型

$X\in (x-ϵ,x+ϵ)$ 的概率

$P(x-ϵ<X<x+ϵ)={\int }_{x-ϵ}^{x+ϵ}f(x|\theta )dx\stackrel{积分中值定理}{}2ϵf(x|{\theta }_{\xi })=2ϵL({\theta }_{\xi }|X)$

极大似然估计

$X$ 独立同分布，$x_1,x_2,\cdots ,x_n$ 选取 $\hat{\theta }(x_1,x_2,\cdots ,x_n)$ 作为 $\theta$ 观测值，使 $P_{\theta }(X=x)=L(\theta |X)$ 的概率最大
$$\begin{array}{r}L(\theta |x_1,x_2,\cdots ,x_n)=arg\underset{\theta }{\max }P(x_1,x_2,\cdots ,x_n|\theta )=\prod _{i=1}^{n}P(x_i|\theta )={\int }_{x_1}^{x_n}f(x|\theta )dx\end{array}$$
求解步骤：

1. 构造似然函数$L(\theta )$
2. 取对 $lnL(\theta )$
3. 求偏导，令 $\frac{dlnL(\theta )}{d\theta }=0$
4. 求 $\hat{\theta }$

eg

$X\sim P(\lambda )$ ，$x_1,\cdots ,x_n$ 为样本值，求 $\lambda$ 极大似然估计

$P(X=k)=\frac{{\lambda }^k}{k!}{e}^{-\lambda },(k=0,1,\cdots ,n)$

$L(\lambda )=\prod _{i=1}^n\frac{{\lambda }^{x_i}}{(x_i)!}{e}^{-\lambda }=e^{-n\lambda }\frac{{\lambda }^{\sum _{i=1}^n{x}_i}}{\prod _{i=1}^n(x_i)!}$

$lnL(\lambda )=-n\lambda +(\sum _{i=1}^n{x}_i)ln\lambda -\sum _{i=1}^{n}ln[(x_i)!]$

令 $\frac{dlnL(\lambda )}{d\lambda }=0\Rightarrow \hat{\lambda }=\frac{1}{n}\sum _{i=1}^n{x}_i=\overline{x}$

模型判别

SML——优化问题

1. 设计模型：概率模型判别
2. Loss function 求解
3. 算法

总结：极大似然参数估计完全依赖本次抽样的样本值

点估计量的评估

无偏性：估计量的数学期望等于未知参数的真实值

• 如果估计量是无偏的，保持估计量的构造不变，而进行多次抽样，每次用新的样本计算估计值，那么这些估计值与未知参数真实值的偏差在平均意义上等于0

有效性：无偏估计量的方差尽量小

• 估计量与真实值之间的偏离程度

一致性：当样本容量趋近于无穷时，估计量依概率收敛于未知参数的真实值

区间估计

在估计未知参数 $\theta$ 的过程中，除了求出估计量，还需估计出一个区间，并且确定这个区间包含 $\theta$ 真实值的可信程度。

• 区间：置信区间

对总体反复抽样多次，每次得到容量相同的样本，根据每一组样本值可以确定一个置信区间 $(\underline{\theta },\overline{\theta })$

每个置信区间有两种可能：包含 $\theta$ 和不包含 $\theta$ 。

如果对所有置信区间中包含 $\theta$ 真实值的比例进行统计，$\frac{包含\theta 的置信区间}{置信区间数总数}$ 为置信水平

在点估计的基础上，增加取指范围(置信区间)、误差界限(置信水平)

3.7.2 贝叶斯派

贝叶斯定理

条件概率

引例

3张抽奖券，1个中奖券，最后一名与第一名抽中奖概率相同

$Y$ ：抽中，$N$ ：未抽中 ,$\Omega =\{YNN,NYN,NNY\}$ ，$A_i$ 事件表示第 $i$ 名抽中

$P(A_3)=\frac{|A_3|}{|\Omega |}=\frac{1}{3}$

$P(A_1)=\frac{|A_1|}{|\Omega |}=\frac{1}{3}$

上例中，若已知第一名未抽中，求第三名抽中概率，则：

第一名未抽中 $B=\{NYN,NNY\}$

第二名抽中 $A_2=\{NNY\}$

$P(A_2|B)=\frac{1}{2}$

---

分析：样本空间变了，目标样本数量不变

事件B发生条件下，有事件A发生 $⟺$ 事件AB同时发生，样本空间为B

求解：

$P(A|B)=\frac{P(AB)}{P(B)}⟺\frac{n(AB)/n(\Omega )}{n(B)/n(\Omega )}=\frac{P(AB)}{P(B)}$

---

eg

掷硬币，100个中有99个正常HT，一个HH。投出去是正面，该硬币是异常硬币的概率

A表示异常硬币的概率，B表示掷出正面的概率

• $P(A|B)=\frac{异常硬币正面}{n(硬币正面)}=\frac{2}{101}$

• $P(A|B)=\frac{P(AB)}{P(B)}=\frac{P(A|B)P(B)}{P(A|B)P(B)+P(A|\overline{B})P(\overline{B})}=\frac{2}{101}$

独立性

若 $P(B|A)=P(B)$ ，则 A、B独立

• 若 $P(A_1,A_2,\cdots ,A_n)=\prod _{i=1}^{n}P(A_i)$ ，则 $A_1$ ，$A_2$ ，$\cdots$，$A_n$ 相互独立

相互独立（整体）$\ne$ 两两独立（两个）
$$\begin{array}{r}P(ABC)=\{\begin{array}{l}相互：P(ABC)=P(A)P(B)P(C)\\ 两两：P(AB)=P(A)P(B),P(BC)=P(B)P(C),P(AC)=P(A)P(C)\end{array}\end{array}$$
独立重复实验：相同条件下，实验E重复进行每次试验结果相互独立

n重伯努利实验：规定实验结果只有 $A$ 和 $\overline{A}$ 两种，相同条件下，将实验独立地重复n次

变式

乘法原理 ：$P(AB)=P(A)P(B)$

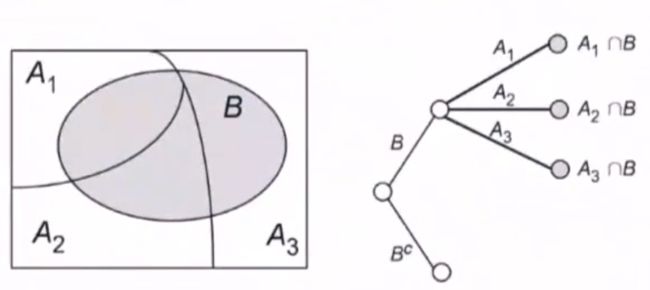
全概率公式

S：实验E中的样本空间，$A_1,\cdots ,A_2$ 为E中一组事件

满足：

• $A_i{A}_j=\varphi$
• $A_1\bigcup A_2\bigcup \cdots \bigcup A_n=S$

则称 $A_1,A_2,\cdots ,A_n$ 为 $S$ 的一个 划分

$P(B)=P(A_1\bigcap B)+\cdots +P(A_n\bigcap B)=P(A_1)P(B|A_1)+\cdots +P(A_n)P(B|A_n)$

贝叶斯公式

先验概率 $P(A_i)$ 与后验概率 $P(A_i|B)$ 关系

$P(A_i|B)=\frac{P(B{A}_i)}{P(B)}=\frac{P(B|A_i)P(A_i)}{P(B)}=\frac{P(B|A_i)P(A_i)}{\sum _{j=1}^{n}P(B|A_j)P(A_j)}$

• 先验：假设(已知条件)的概率
• 后验：已知结果得到条件的概率

贝叶斯定理

$$P(H|D)=\frac{P(D|H)P(H)}{P(D)}$$

• $P(H)$ ：先验概率
• $P(D|H)$ ：似然概率
• $P(H|D)$ ：后验概率

贝叶斯定理计算概率

贝叶斯估计

后验($数据\to 参数$) $\to$ 先验（$参数\to 数据$）

在贝叶斯估计中，参数 $\theta$ 为关注部分，以 $\theta$ 作为前提的条件概率为先验概率

结合先验知识（统计，频数），若样本不合理可进行校正
$$\begin{array}{rl}{\theta }_{MAP}& =arg\underset{\theta }{\max }P(\theta |X)=arg\underset{\theta }{\max }\frac{P(X|\theta )P(\theta )}{P(X)}\\ & \stackrel{同一样本不同模型，数据出现概率相等，P(X)可看做常数，进而忽略}{}\\ & \propto arg\underset{\theta }{\max }P(X|\theta )P(\theta )\end{array}$$
样本离散：
$$\begin{array}{rl}arg\underset{\theta }{\max }P(X|\theta )P(\theta )& =arg\underset{\theta }{\max }P(x_1,x_2,\cdots ,x_n|\theta )P(\theta )=arg\underset{\theta }{\max }\left[\prod _{i=1}^{n}P(x_i|\theta )\right]P(\theta )\\ & =arg\underset{\theta }{\max }ln\left\{\left[\prod _{i=1}^{n}P(x_i|\theta )\right]P(\theta )\right\}\\ & =arg\underset{\theta }{\max }\left[\sum _{i=1}^{n}lnP(x_i|\theta )+lnP(\theta )\right]\end{array}$$
样本连续：

$arg\underset{\theta }{\max }P(X|\theta )P(\theta )=arg\underset{\theta }{\max }P(x_1,x_2,\cdots ,x_n|\theta )P(\theta )=arg\underset{\theta }{\max }{\int }_{\theta }P(X|\theta )P(\theta )$

---

eg

拼写检查 $P(猜测词|实际输入词)$

猜测1：$P(w_1|D)$ ，猜测2：$P(w_2|D)$

$P(w|D)=\frac{P(w)P(D|w)}{P(D)}$ ，在已有输入的情况下，不管正确词是哪种情况，输入词出现的概率 $P(D)$ 都相同

• 出于无法估计/估计困难，忽略同一影响 $P(D)$

故 $P(w|D)\propto P(D|w)P(w)$

此时，$P(w)$ 为先验知识，可以通过统计，得出正确词出现的概率

若输入 tlp ，对于 $top$ 或 $tip$ ，用极大似然无法估计，但由统计学，用户输入 $top$ 词频高，则 top 概率大，$P{(}^{\prime }to{p}^{\prime }{|}^{\prime }tl{p}^{\prime })>P{(}^{\prime }to{p}^{\prime }{|}^{\prime }tl{p}^{\prime })$

贝叶斯预测

$X$：训练数据，$X$ ：测试数据

$P(X|X)={\int }_{\theta }P(X,\theta |X)d\theta ={\int }_{\theta }P(X|\theta )P(\theta |X)d\theta$

• $P(\theta |X)$ ：由训练数据得到某一模型
• $P(X|\theta )$ ：某一模式下，测试数据出现的概率

模型比较理论

极大似然：最符合观测数据的最有优势，$P(D|\theta )$

奥卡姆剃刀：$P(\theta )$ 先验概率大的模型最有优势

eg ：对于平面上点进行拟合，根据奥卡姆剃刀原理，越高阶多项式越不常见（过拟合线性）

$P(Pol(X))\ll P(Pol(2))\ll P(Pol(1))$

实例：垃圾邮件过滤

$D$ ：邮件，$D$ 由 $n$ 个单词组成，$h^{+}$ ：垃圾邮件，$h^{-}$ ：正常邮件

$P(h^{+}|D)=\frac{P(D|h^{+})P(h^{+})}{P(D)}\propto P(h^{+})P(D|h^{+})$

$P(h^{-}|D)=\frac{P(D|h^{-})P(h^{-})}{P(D)}\propto P(h^{-})P(D|h^{-})$

先验概率： $P(h^{+})$ 与 $P(h^{-})$ 都可以通过统计学得出，

$D$ 中包含 $n$ 个词，$d_1,d_2,\cdots ,d_n$ ，$P(D|h^{+})=P(d_1,d_2,\cdots ,d_n|h^{+})$ 为垃圾邮件中出现这些词的概率

$$\begin{array}{rl}(原始贝叶斯)& P(d_1,d_2,\cdots ,d_n|h^{+})=P(d_1|h^{+})P(d_2,\cdots ,d_n|d_1,h^{+})=\cdots =P(d_1|h^{+})P(d_2|d_1,h^{+})P(d_3|d_1,d_2,h^{+})\cdots \\ \Downarrow & \\ (朴素贝叶斯)& \stackrel{假设特征间相互独立}{}P(d_1|h^{+})P(d_2|h^{+})\cdots P(d_n|h^{+})\end{array}$$

可以用频率代替概率