【博弈论】第二讲：纳什均衡的混合战略（有限数量战略）

1. 原则一:战略的保密性与随机性
2. 原则二:不能给对方以可乘之机（对方选择A和B，或者C和D的收益没有差别，就是不给对方可乘之机）

混合战略概念

在$n$个参与人的博弈$G=\left\{S_1，...，S_n;u_1，...，u_n\right\}$中，参与人$i$的战略空间为$S_{,}=\left\{S_1\dots ,S_i\right\}$，则参与人i以概率分布$p_i=(p_{i1},\dots ,p_{ix})$随机选择其$k$个可选战略称为一个“混合战略”，其中$0\le p_{ik}\le 1$且$p_{i1}+\dots +p_{ik}=1$。

• 纯战略(pure strategies):如果一个战略规定参与人在一个给定的信息情况下只选择一种特定的行动。
• 混合战略(mixed strategies):如果一个战略规定参与人在给定的信息情况下，以某种概率分布随机地选择不同的行动。
• 在静态博弈里，纯战略等价于特定行动，混合战略是不同行动之间的随机选择。

混合战略的期望收益求解

与混合战略(mixed strategies)相伴随的一个问题,是参与人支付的不确定(uncertainty)。可用期望支付(expected payoff)来描述:有n个可能的取值X,Xg…,Xn，并且这些取值发生的概率分别为p,P2.…., pn，那么可以将这个数量指标的期望值定义为发生概率作为权重的所有可能取值的加权平均，也就是
$$E{U}_A=p_1{x}_1+p_2{x}_2+\dots +p_n{x}_n$$

【例题】

政府和流浪汉的博弈
政府想帮助流浪汉,但前提是后者必须试图寻找工作，否则不予帮助;而流浪汉若知道政府采用救济战略的话，他就不会寻找工作。他们只有在得不到政府救济时才会寻找工作。他们获得的支付如图所示:

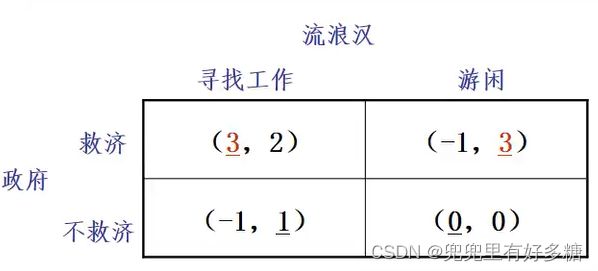
通过观察划线法可以得知：没有一个双划线的得益数组，也就是没有一个纯战略纳什均衡，也就是政府没有一个最好的选择，流浪汉也没有一个最好的选择。
在这样一种情况下我们仍然要确定各自的一个行为选择的时候我们就采用混合战略方式。

假定政府采用混合战略：选择救济的概率是$\theta$，不救济的概率是$1-\theta$。
流浪汉的混合战略是：选择找工作的概率：$\gamma$，游闲的概率：$1-\gamma$
$${\delta }_G=(\theta ,1-\theta ){\delta }_L=(\gamma ,1-\gamma )$$

有一种求纳什均衡的办法是：我们要求支付最大化

政府的期望效用函数是：
$$v_G\left({\delta }_G,{\delta }_L\right)=\theta [3\gamma +(-1)(1-\gamma )]+(1-\theta )[-\gamma +0(1-\gamma )]=\theta (5\gamma -1)-\gamma$$
政府最优化的一阶条件为：$\frac{\partial v_G}{\partial \theta }=5\gamma -1=0\Rightarrow {\gamma }^{\ast }=0.2$
流浪汉的期望效用函数为：
$$v_L\left({\delta }_G,{\delta }_L\right)=\gamma [2\theta +1(1-\theta )]+(1-\gamma )[3\theta +0(1-\theta )]=-\gamma (2\theta -1)+3\theta$$
流浪汉最优化的一阶条件为：$\frac{\partial v_L}{\partial \gamma }=-(2\theta -1)=0\Rightarrow {\theta }^{\ast }=0.5$

上面这种求导来求最大值的算法其实有点不符合数学的逻辑，另一个问题是我们求政府的支付最大化求出的却是$\gamma$的最大值，求流浪汉的最大支付函数求出的却是$\theta$，都是相反的。所以这一点也比较反常识一点。

还有一种方法是支付等值法：

就是完全利用我们一开始提到的原则：
找不到纯战略的情况下，就选择让对方无机可乘。也就是参与人一选择某个方案，会让参与人二选择A方案与选择B方案的收益是无差异的。就称之为等值法。

• 如果政府选择救济策略：$\theta =1$，那么他这时候的期望收益是：
  $$\begin{array}{rl}& v_G(1,\gamma )=3\gamma +(-1)(1-\gamma )\\ & =4\gamma -1\end{array}$$

• 政府如果选择不救济策略：$\theta =0$，这时候政府的期望效用是
  $$\begin{array}{rl}& v_G(0,\gamma )=-1\gamma +0(1-\gamma )\\ & =-\gamma \end{array}$$
  如果一个混合战略是流浪汉的最优选择，那一定意味着政府在救济与不救济之间是无差异的，即:
  $$\begin{array}{rl}& v_G(1,\gamma )=4\gamma -1=-\gamma =v_G(0,\gamma )\\ & \Rightarrow {\gamma }^{\ast }=0.2\end{array}$$
  可以看出与求导数方法算出的结果是一样的。
  同理：如果一个混合战略是政府的最优选择，那一定意味着流浪汉在寻找工作与游闲之间是无差异的，即:
  $$\begin{array}{rl}& v_L(1,\theta )=1+\theta =3\theta =v_L(0,\theta )\\ & \Rightarrow {\theta }^{\ast }=0.5\end{array}$$

• 如果政府救济的概率小于0.5;则流浪汉的最优选择是寻找工作

• 如果政府救济的概率大于0.5; 则流浪汉的最优选择是游闲等待救济

• 如果政府救济的概率正好等于0.5;流浪汉的选择无差异

第三种方法是反应曲线法（如何应对是最佳反应）

【例】假设甲、乙均采用混和战略,随机地以$p$的概率出红牌和以$(1-p)$的概率出黑牌,而乙则随机地以$q$的概率出红牌和以$(1-q)$的概率出黑牌。

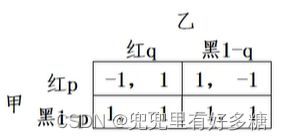
先把每个人的总期望收益写出来。

• 甲的期望支付是：
  $$U_A(p,q)=(-1)[pq+(1-p)(1-q)]+1[p(1-q)+(1-p)q]=2p(1-2q)+(2q-1)$$
  （最后整理成一部分和$p$有关的，一部分和$p$无关的）
• 乙的期望支付是：
  $$U_B(p,q)=1[pq+(1-p)(1-q)]+(-1)[p(1-q)+(1-p)q]=2q(1-2p)+(2p-1)$$
  （最后整理成一部分和$q$有关的，一部分和$q$无关的）

$A$的目标是期望支付越大越好。之所以把$A$的期望支付整理成不含$p$的一项和含$p$的一项，是因为$A$只能选择$p$而不能$q$，因此，$A$能通过选择$p$来影响第一项，而不能直接影响第二项。$(1-2q)>0$即$q<1/2$时，$A$把$p$选择等于1最好;当$(1-2q)<0即q>1/2$时，$A$把$p$选择等于$0$最好;当$(1-2q)=0$即$q=1/2$时，$A$可以在$[0，1]$之间随便选择一个$p$。这样我们可以得到$A$的反应函数，同样道理我们可以得到$B$的反应函数。
$$p=\{\begin{array}{cl}0,& \text{ 如果 }\mathrm{q}>1/2\\ [0,1],& \text{ 如果 }\mathrm{q}=1/2\\ 1& \text{ 如果 }\mathrm{q}<1/2\end{array}$$
$$q=\{\begin{array}{cl}1,& \text{ 如果 }\mathrm{p}>1/2\\ [0,1],& \text{ 如果 }\mathrm{p}=1/2\\ 0& \text{ 如果 }\mathrm{p}<1/2\end{array}$$
根据上面的分段等式，可以画出下面这这副反应曲线图（红色曲线是A对B的反应，粉色曲线是B对A的反应）。所以求纳什均衡就是求双方对对方的最优反应，那就是两条反应曲线的交点处，也就是$(1/2,1/2)$。

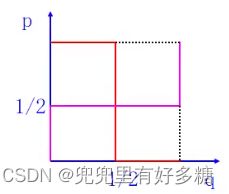
求混合战略均衡要先剔除劣战略：

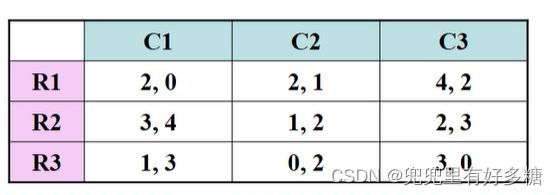
我们用第二种方法来讨论这个问题：就是讨论参与人2选择$C_1,C_2,C_3$的概率分别是多少的时候，参与人1选择$R_1,R_2,R_3$的期望效用无差异：
设想$C$以$p$的概率选择$C_1$，以$q$的概率选择$C_2$，以$1-p-q$的概率选择$C_3$;则对于$R$而言:
选择$R_1$的预期效用为：
$$2p+2q+4(1-p-q)=4-2p-2q$$
选择$R_2$的预期效用为：
$$3p+q+2(1-p-q)=2+p-q$$
选择$R_3$的预期效用为：
$$p+3(1-p-q)=3-2p-3q$$
如果我们用第二种方法算纳什均衡，也就是支付等值法，那么就令$R_1$的期望收益值与$R_2$的以及$R_3$的都相等，从而可以解出：
$$\begin{gathered} p=1 \\ q=-1 \end{gathered}$$
但是这显然是不符合客观规律的，因为算出的概率不应该是负值，负值是没有意义的。
问题出在哪里？
在于我们这个图中所显示的所有战略里面有一个严格劣战略，而这个劣战略就是参与人不可能选择的战略，所以它的概率应该是0，但是你现在非说他的概率是$p$或者是$q$，就出问题了。所以在进行混合战略的求解之前一定要先把严格劣战略剔除掉！！！

【例题】【广告决策】

三家公司同时决定是在早间还是晚间投放广告。如果同时间有多家公司做广告，他们的收益均为0;如果仅有一家公司在早间做广告，其收益为1;如果仅有一家公司在晚间做广告，其收益为2。证明如果存在混合战略纳什均衡，那么它是唯一的，并求出该均衡。
【解】
设某一家公司在早上投放广告的概率是$P$，在晚上投放广告的概率是$1-P$。
计算早上投放的总收益值：

• 一家在早上投放
  如果只有一家在早上投放广告，则期望收益值是1。并且意味着与此同时另外两家公司必须在晚上投放广告，所以这种可能性的概率是$P\ast (1-P)\ast (1-P)$，其收益只有1，所以总收益是$P\ast (1-P)\ast (1-P)\ast 1$。
• 还有一种是有两家在早上，一家在晚上；或者三家在早上，没有公司在晚上。由于这两种情况下收益均是0，所以就不用算了。

所以综合以上几种情况，在早上投放广告的总期望收益是$P\ast (1-P)\ast (1-P)\ast 1+0+0=P\ast (1-P)\ast (1-P)$。
下面计算在晚上投放广告的总期望收益：

• 只有一家在晚上投放广告
  意味着另外两家都在早上投放广告，所以这种情况的概率是：$P\ast P\ast (1-P)$，这种情况的收益是2。所以这种情况的总收益是：$P\ast P\ast (1-P)\ast 2$.

• 还有一种情况是有两家在晚上投放广告，这时晚上的收益仍然为0。所以晚上的总收益就是$P\ast P\ast (1-P)\ast 2$。

• 支付等值法让早上的收益等于晚上的收益即可。

【例题】

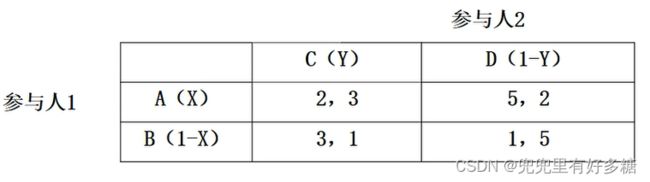
解：与上题相同，我们可以写出基于概率的双方的支付函数：
$$\begin{array}{rl}{u}_1& =2XY+5X(1-Y)+3(1-X)Y+(1-X)(1-Y)\\ & =4X+2Y-5XY+1\\ u_2& =3XY+2X(1-Y)+(1-X)Y+5(1-X)(1-Y)\\ & =5XY-3X-4Y+5\end{array}$$
然后求导求出令支付函数取得最大值的概率：
$$\begin{array}{ll}\frac{d{u}_1}{dX}=0& \frac{d{u}_2}{dY}=0\\ \Rightarrow 4-5Y=0& \Rightarrow 5X-4=0\\ \Rightarrow Y=0.8& \Rightarrow X=0.8\end{array}$$

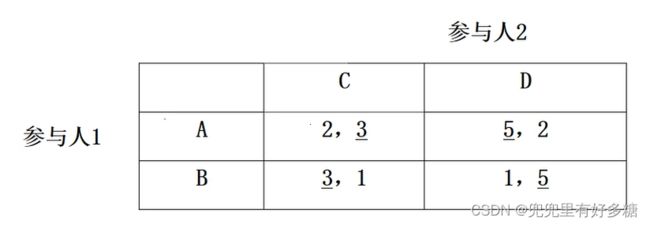
【例题】

设参与人1选$A$的概率为$p_A$，选$B$的概率为$p_B$，参与人2选$C$的概率为$p_C$，选$D$的概率为$p_D$。根据上述第二个原则，参与人1选$A$和$B$的概率$p_A$和$p_B$。一定要使参与人2选$C$的期望得益和选$D$的期望得益相等，即:
$$p_A\times 3+p_B\times 1=p_A\times 2+p_B\times 5p_A+p_B=1p_A=0.8,p_B=0.2$$
$$p_C\times 2+p_D\times 5=p_C\times 3+p_D\times 1p_C+p_D=1p_C=0.8,p_D=0.2$$

【税收检查】

• 应纳税额：$a$
• 检查成本：$C$
• 罚款：$F$
• 用$\theta$代表税收机关检查的概率，$\gamma$代表纳税人逃税的概率。
  
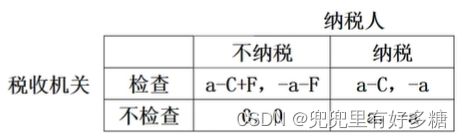
• 税收机关选择检查和不检查的期望收益为:
  $$\begin{array}{rl}& (a-C+F)\gamma +(a-C)(1-\gamma )=0\gamma +a(1-\gamma )\\ & \gamma =\frac{C}{a+F}\end{array}$$
• 纳税人选择逃税和不逃税的期望收益分别为:
  $$\begin{array}{rl}& -(a+F)\theta +0(1-\theta )=-a\\ & \theta =\frac{a}{a+F}\end{array}$$
  我们可以根据三个参数对$\theta$和$\gamma$的影响来知道我们的政策倾向。

【例题】【小偷与守卫】

泽尔腾（1996年3月，上海):一小偷欲偷窃有一守卫看守的仓库，如果小偷偷窃时守卫在睡觉，则小偷就能得手，偷得价值为$V$的赃物;如果小偷偷窃时守卫没有睡觉，则小偷就会被抓住。设小偷被抓住后要坐牢，负效用为$-P$，守卫睡觉而未遭偷窃有$S$的正效用，因睡觉被窃要被解雇，其负效用为$-D$。而如果小偷不偷，则他既无得也无失，守卫不睡意味着出一份力挣一份钱，他也没有得失。根据上述假设，小偷在该博弈中有“偷”和“不偷”两种可选战略，守卫有“睡”和“不睡”两种可选战略，双方的得益矩阵如图。

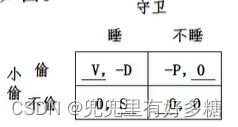
【解】
本题我们使用数形结合的办法做，画出图：

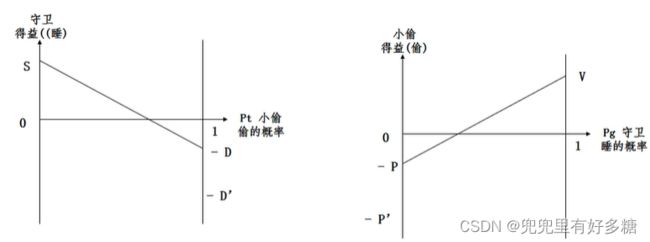
如何求小偷的最大收益呢？那就是对小偷而言，守卫睡觉和不睡觉的期望收益相等。由于守卫睡觉的期望收益是0，因此就是左图中的斜线与横轴交点的位置，就是小偷的最佳决策点，因为这时候不论守卫是否睡觉，守卫的收益都是0。
同理，右侧守卫的最佳决策点也是斜线与横轴的交点位置，此位置处，不论小偷偷或者不偷，其收益都是0。
由此图我们不仅可以获得上述的一些结论，也可以获取一些对于政策的指导：
如下图的左图，如果我们加重对守卫睡觉的惩罚，则左图的右侧降低，斜线的斜率增大，会使得斜线与横轴的交点左移，代表着小偷偷窃的改率降低。
对于右图：如果加重对偷窃失败的小偷的惩罚，则左侧下降，斜线斜率增大，斜线与横轴的交点右移，代表守卫睡觉的概率会增大。

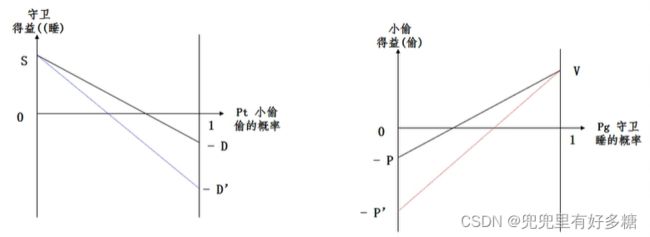
加重对守卫的处罚:短期中的效果是使守卫真正尽职。在长期中并不能使守卫更尽职，但会降低盗窃发生的概率。
但是加重对小偷的处罚，会增大守卫不尽职的概率。所以加重对小偷的惩罚是治标不治本的举动。

【例题】（考试题）

参与人1、2针对一个奖品进行博弈争夺。为了获胜，参与人1选择了X的努力水平,参与人2则选择了$Y$的努力水平$(X,Y\ge 0)$。这时参与人1获胜的概率为$X/(X+Y)$,参与人2获胜的概率为$Y/(X+Y)$。该奖品的价值为10，每一单位努力的成本为1。若两人同时决定努力水平,则纳什均衡为:
A.(2,2) B.(2.5,2.5)
C.(3,3) D.(3.5,3.5)
【解】
参与人一的期望效用是：
$10\ast X/(X+Y)(收益)-X\ast 1(成本)$
参与人二的期望效用是：
$10\ast Y/(X+Y)(收益)-Y\ast 1(成本)$
每个人都希望自己的期望效益最大化，所以就是每个人对各自的努力程度求偏导，让偏导等于0即可：
$$\{\begin{array}{cl}\frac{d(10\ast X/(X+Y)-X\ast 1)}{dX}=0,& \text{ (参与人一 )}\\ & \\ \frac{d(10\ast Y/(X+Y)-Y\ast 1)}{dY}=0,& \text{ (参与人二 )}\end{array}$$

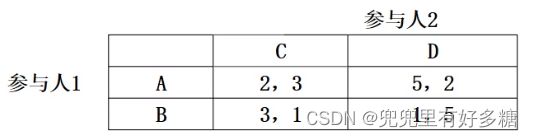
【例题】试用支付最大化法、支付等值法、反应曲线法,求下列矩阵表示的完全相信静态博弈的纳什均衡。

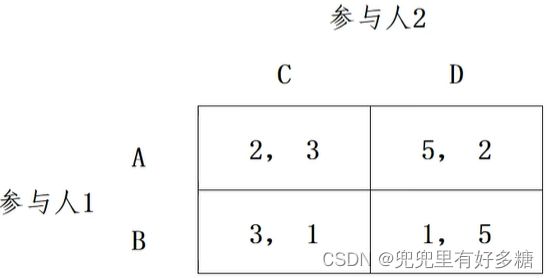
设参与人1选择A的概率为X，则选择B的概率为1-X;参与人2选择C的概率为Y，则选择D的概率为1-Y.
(1)支付最大化法:
参与人1的期望效用为：
$${\mathrm{EU}}_1=2\mathrm{XY}+5\mathrm{X}(1-\mathrm{Y})+3(1-\mathrm{X})\mathrm{Y}+1(1-\mathrm{X})(1-\mathrm{Y})=1+4\mathrm{X}+2\mathrm{Y}-5\mathrm{XY}$$
$$\text{ 令 }\frac{dEU1}{dX}=0\text{ 得 }4-5Y=0\text{ 得 }Y=0.8$$
参与人二的期望效用为：
$${\mathrm{EU}}_2=3\mathrm{XY}+2\mathrm{X}(1-\mathrm{Y})+1(1-\mathrm{X})\mathrm{Y}+5(1-\mathrm{X})(1-\mathrm{Y})=5-3\mathrm{X}-4\mathrm{Y}+5\mathrm{XY}$$
$$\text{ 令 }\frac{\mathrm{dEU}2}{\mathrm{dY}}=0\text{ 得 }-4+5X=0\text{ 得 }X=0.8$$
所以，纳什均衡为{(0.8,0.2),(0.8,0.2)}。
(2)支付等值法：
参与人1选择$A$的收益为:$EA=2Y+5(1-Y)=5-3Y$
参与人1选择$B$的收益为:$EB=3Y+1(1-Y)=1+2Y$
由收益无差异得$EA=EB$即$15-3Y=1+2Y$得$Y=0.8$
参与人2选择$C$的收益为:$EC=3X+1(1-X)=1+2X$
参与人2选择$D$的收益为:$ED=2X+5(1-X)=5-3X$由收益无差异得$EC=ED即1+2X=5-3X$得$X=0.8$
所以，纳什均衡为{(0.8，0.2) ,(0.8,0.2)}
(3)反应函数（曲线）法：
参与人1的期望效用为：
$$\begin{array}{rl}{\mathrm{EU}}_1& =2\mathrm{XY}+5\mathrm{X}(1-\mathrm{Y})+3(1-X)Y+1(1-X)(1-Y)\\ & =(4-5\mathrm{Y})\mathrm{X}+(1+2\mathrm{Y})\end{array}$$
参与人2的期望效用为：
$$\begin{array}{rl}{\mathrm{EU}}_2& =3\mathrm{XY}+2\mathrm{X}(1-\mathrm{Y})+1(1-X)Y+5(1-X)(1-Y)\\ & =(-4+5X)Y+(5-3X)\end{array}$$
所以，纳什均衡为{(0.8,0.2),(0.8,0.2)}。
每种计算方法得到的期望收益为(2.6,2.6)。

【例题】求职博弈

企业1、2各有一个工作空缺，企业$i$的工资为$W_i$，且$\frac{1}{2}{w}_1<w_2<2w_1$。设有两人同时决定申请这两个企业的工作，规定每人只能申请一份工作。如果一个企业的工作只有一人申请，该人肯定得到这份工作;如果一个企业的工作同时有两人申请，则企业随机选择一人，另一人就会因为错过向另一个企业申请的时机而失去工作（此时收益为0）。问该博弈的纳什均衡是什么?该博弈的结果有多少种可能性，各自的概率是多少?
【解】
注意博弈的主体是求职者而不是企业。

【例题】支撑求解法求混合战略纳什均衡

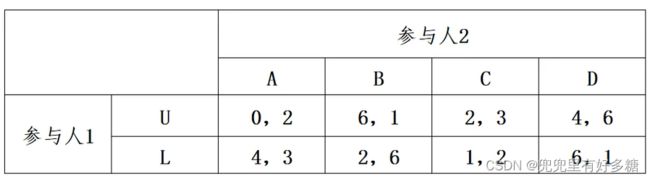
【解】
这种非22的战略集合，可能导致他的矩阵的值比方程个数要少，导致最终求不出解的问题。
如果求不出解，我们就要考虑降维，将这样一个24的战略集合降维称为23的或22的，然后看看是否能求出符合要求的解：
$|\mathrm{U},\mathrm{L}|\times |A,B,C||\mathrm{U},\mathrm{L}|\times |A,B,D|$
$|\mathrm{U},\mathrm{L}|\times |A,C,D||\mathrm{U},\mathrm{L}|\times |B,C,D|$
$|\mathrm{U},\mathrm{L}|\times |A,D||\mathrm{U},\mathrm{L}|\times |B,C||\mathrm{U},\mathrm{L}|\times |B,D||\mathrm{U},\mathrm{L}|\times |C,D||\mathrm{U},\mathrm{L}|\times |A,B||\mathrm{U},\mathrm{L}|\times |A,C|$

首先我们来看2*4的情况下有没有合适的解，有没有纳什均衡：
$|\mathrm{U},\mathrm{L}|\times |A,B,C,D|$
根据战略列表，我们可以写出如下的式子：
$\{\begin{array}{l}6B+2C+4D=U_1\\ 4A+2B+C+6D=U_1\\ 2U+3L=U_2\\ U+6L=U_2\\ 3U+2L=U_2\\ 6U+L=U_2\\ A+B+C+D=1\\ U+L=1\end{array}$
解这个方程组会发现没有一个固定解，所以肯定要用到降维了。

然后我们依次讨论三种降维成2*3的战略组合是否有稳定解：发现一样得不到有效解。

最后我们看2*2的战略组合是否有有效解：
我们发现$|\mathrm{U},\mathrm{L}|\times |A,B|$这个战略组合可以解出一个有效解：
$$\{\begin{array}{l}6B=U_1\\ 4A+2B=U_1\\ 2U+3L=U_2\\ U+6L=U_2\\ A+B=1\\ U+L=1\end{array}$$
解出的结果是：
$A=B=1/2,U=3/4,L=1/4。U_1=3,U_2=9/4(1的期望收益值是3，2的期望收益值是9/4)$
但我们同时发现一个问题，当$U=3/4,L=1/4$时，我们计算$C$战略的收益值为：$U(C)=11>U_2$。也即C的收益比$A，B$都更大，所以参与人1按照这样的概率来选择$U$和$L$时，参与人一有不在$A，B$战略中考虑的倾向，比如就有考虑$C$战略的倾向。因为C的收益要比A，B收益高。
所以这种降维虽然能算出结果，但是求出的解不稳定，就是说这种仅考虑A，B，而把其他战略概率看成0的降维方法得到的结果是不好的，不稳定的。因为算出的结果是参与人1有动机选择C，所以你降维的假设：”选择C的概率为0“就不成立了。所以即使这种算出了有一个解，但却并不是稳定解。
同样的我们去分析其他的战略组合，得到的结果也是一样的，最终都会和假设相矛盾。
最终只有一组：$|\mathrm{U},\mathrm{L}|\times |B,D|$算出来的这个解是符合纳什均衡的唯一解且是稳定解：
$$\{\begin{array}{l}6B+4D=U_1\\ 2B+6D=U_1\\ U+6L=U_2\\ 6U+L=U_2\\ B+D=1\\ U+L=1\end{array}\Rightarrow \{\begin{array}{l}B=1/3\\ D=2/3\\ U=L=1/2\Rightarrow \text{ 混合均衡解 }\\ U_1=14/3\\ U_2=7/2\end{array}$$