Apache Commons Math: 面向Java的数学和统计库

第1章：引言

大家好，我是小黑，咱们今天要聊的是Apache Commons Math这个宝藏级的Java库。为啥说它是宝藏呢？因为它简直就是处理数学问题的瑞士军刀，无论你是要搞统计分析、数值计算，还是解决优化问题，这个库都能来一把。小黑今天就带大家深入浅出地了解一下它的魅力所在。

咱们处理数据不可避免地会遇到各种数学问题。这时候，如果每次都从头开始写，那得多累啊。这就像是每次做菜都要先种菜一样，效率低下不说，还容易出错。Apache Commons Math就像是厨房里的调料，帮你迅速地解决这些数学方面的难题。

那么，Apache Commons Math到底是个啥？简单来说，它是一个开源的Java库，提供了一大堆数学和统计方面的函数。你要做一些复杂的数学计算，或者是统计分析？没问题，这个库都能帮到你。它就像是数学界的瑞士军刀，无论你遇到什么问题，总能找到合适的工具。

第2章：Apache Commons Math概览

说到Apache Commons Math，这个库可是有着丰富的历史和背景。它是Apache Software Foundation旗下的一个项目，一直以来都致力于为Java开发者提供高质量的数学计算工具。它的目标就是让复杂的数学计算变得简单，让开发者能更专注于业务逻辑的实现。

Apache Commons Math包含了很多模块，每个模块都针对特定的数学或统计需求。比如说，它有线性代数模块，提供了各种矩阵运算的工具；还有统计模块，可以帮你做描述性统计、概率分布的计算；当然，也少不了优化算法，比如非线性优化、多目标优化等等。

讲到这里，可能有的小伙伴会问，这些听起来都很高大上，但具体能干嘛呢？小黑这就给咱们来个实例。比如说，咱们要计算一组数据的平均值、最大值、最小值。这可是统计分析中的基本操作，用Apache Commons Math就能轻松搞定。

下面是个简单的Java代码示例，咱们一起看看：

import org.apache.commons.math3.stat.descriptive.DescriptiveStatistics;

public class StatisticsExample {
    public static void main(String[] args) {
        // 创建统计对象
        DescriptiveStatistics stats = new DescriptiveStatistics();

        // 加入一些数据
        stats.addValue(5.0);
        stats.addValue(3.0);
        stats.addValue(8.0);

        // 计算平均值、最大值和最小值
        double mean = stats.getMean(); // 平均值
        double max = stats.getMax();   // 最大值
        double min = stats.getMin();   // 最小值

        // 输出结果
        System.out.println("平均值: " + mean);
        System.out.println("最大值: " + max);
        System.out.println("最小值: " + min);
    }
}

在这段代码中，咱们首先引入了Apache Commons Math的DescriptiveStatistics类。这个类就像是统计学的小助手，能帮咱们快速计算一些基本的统计指标。然后，咱们向这个小助手里面添加了一些数据，最后就能得到平均值、最大值和最小值了。

第3章：核心功能深入探讨

3.1 线性代数模块

线性代数，在数学和工程领域可是个大头目。但别担心，Apache Commons Math提供了一整套工具来处理矩阵运算、解线性方程组这些任务。

来，看个例子。比如说，咱们有个线性方程组，想找到它的解。用Apache Commons Math就能轻松搞定。

import org.apache.commons.math3.linear.Array2DRowRealMatrix;
import org.apache.commons.math3.linear.DecompositionSolver;
import org.apache.commons.math3.linear.LUDecomposition;
import org.apache.commons.math3.linear.RealVector;
import org.apache.commons.math3.linear.ArrayRealVector;

public class LinearAlgebraExample {
    public static void main(String[] args) {
        // 定义一个2x2的矩阵
        double[][] matrixData = { {1, 2}, {3, 4} };
        Array2DRowRealMatrix matrix = new Array2DRowRealMatrix(matrixData);

        // 定义方程组右侧的常数项
        double[] vectorData = {5, 11};
        RealVector vector = new ArrayRealVector(vectorData);

        // 使用LU分解来解方程
        DecompositionSolver solver = new LUDecomposition(matrix).getSolver();
        RealVector solution = solver.solve(vector);

        // 打印解
        System.out.println("方程组的解: " + solution);
    }
}

在这段代码里，小黑首先定义了一个2x2的矩阵和一个常数向量，这就是咱们的方程组。然后用LU分解方法求解。这只是线性代数模块的冰山一角，还有很多其他的功能，比如特征值计算、矩阵运算等等。

3.2 统计分析模块

接下来是统计分析。在数据分析和科学研究中，统计是个重要角色。Apache Commons Math提供了一整套统计工具，包括描述性统计、概率分布、假设检验等。

举个例子，如果咱们想要对一组数据进行基本的统计分析，比如计算平均值、方差等，可以这样做：

import org.apache.commons.math3.stat.descriptive.DescriptiveStatistics;

public class StatisticsAnalysisExample {
    public static void main(String[] args) {
        DescriptiveStatistics stats = new DescriptiveStatistics();

        // 加入一些数据
        stats.addValue(1.2);
        stats.addValue(2.3);
        stats.addValue(3.4);

        // 计算统计量
        double mean = stats.getMean(); // 平均值
        double variance = stats.getVariance(); // 方差

        // 打印结果
        System.out.println("平均值: " + mean);
        System.out.println("方差: " + variance);
    }
}

这里咱们用DescriptiveStatistics类来进行计算。只要往里面加数据，然后调用相应的方法就能得到结果。

3.3 数值分析模块

数值分析在科学计算中扮演了重要角色。Apache Commons Math的数值分析功能强大，包括数值积分、微分、插值等。

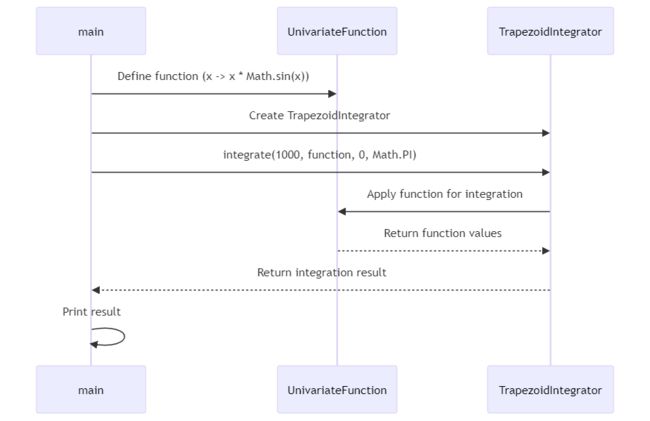
比如说，咱们想计算一个函数的积分，可以用下面的代码：

import org.apache.commons.math3.analysis.integration.TrapezoidIntegrator;
import org.apache.commons.math3.analysis.UnivariateFunction;

public class NumericalAnalysisExample {
    public static void main(String[] args) {
        UnivariateFunction function = x -> x * Math.sin(x); // 定义函数

        TrapezoidIntegrator integrator = new TrapezoidIntegrator();
        double result = integrator.integrate(1000, function, 0, Math.PI); // 计算0到π的积分

        System.out.println("积分结果: " + result);
    }
}

在这里，咱们定义了一个函数，然后用梯形法计算了它在0到π区间内的积分。

3.4 优化算法模块

最后来看看优化算法。在工程和科学研究中，优化问题无处不在。Apache Commons Math提供了多种优化算法，比如非线性优化、多目标优化等。

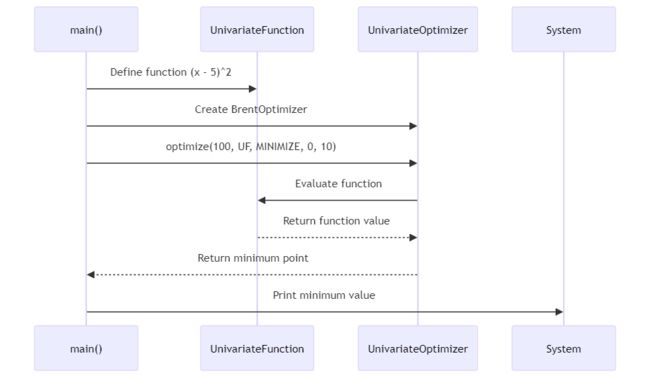
假设咱们有个优化问题，想要找到函数的最小值，可以用以下代码：

import org.apache.commons.math3.optimization.univariate.UnivariateOptimizer;
import org.apache.commons.math3.optimization.univariate.BrentOptimizer;
import org.apache.commons.math3.optimization.GoalType;

public class OptimizationExample {
    public static void main(String[] args) {
        UnivariateFunction function = x -> (x - 5) * (x - 5); // 定义函数

        UnivariateOptimizer optimizer = new BrentOptimizer(1e-10, 1e-14);
        double min = optimizer.optimize(100, function, GoalType.MINIMIZE, 0, 10).getPoint(); // 在0到10范围内寻找最小值

        System.out.println("最小值位于: " + min);
    }
}

这里使用了Brent算法来找到函数在0到10范围内的最小值。这只是优化模块的一小部分，它还有很多其他强大的功能等着咱们去探索。

第4章：实战应用示例

4.1 处理统计数据

假设咱们正在处理一组用户的年龄数据，想要了解这个数据集的一些基本统计信息。这时，Apache Commons Math的统计模块就能派上用场。

import org.apache.commons.math3.stat.descriptive.DescriptiveStatistics;

public class UserAgeStatistics {
    public static void main(String[] args) {
        DescriptiveStatistics stats = new DescriptiveStatistics();

        // 添加一些用户年龄数据
        int[] ages = {23, 30, 34, 45, 36, 28, 55, 40, 31, 29};
        for (int age : ages) {
            stats.addValue(age);
        }

        // 计算并输出统计信息
        System.out.println("平均年龄: " + stats.getMean());
        System.out.println("年龄中位数: " + stats.getPercentile(50));
        System.out.println("年龄标准差: " + stats.getStandardDeviation());
    }
}

在这个例子中，我们创建了DescriptiveStatistics对象，用它来计算年龄数据的平均值、中位数和标准差。这样一来，我们就能快速了解这组数据的分布情况了。

4.2 曲线拟合与预测

再来看一个曲线拟合的例子。假设我们有一些观测数据，想要找到一条曲线来描述这些数据的趋势。Apache Commons Math的曲线拟合功能就能帮到我们。

import org.apache.commons.math3.fitting.PolynomialCurveFitter;
import org.apache.commons.math3.fitting.WeightedObservedPoints;

public class CurveFittingExample {
    public static void main(String[] args) {
        WeightedObservedPoints points = new WeightedObservedPoints();
        // 添加一些观测数据
        points.add(1, 2.3);
        points.add(2, 4.5);
        // ...可以添加更多点

        // 使用二次多项式拟合
        PolynomialCurveFitter fitter = PolynomialCurveFitter.create(2);
        double[] coeffs = fitter.fit(points.toList());

        // 输出拟合结果的多项式系数
        System.out.println("拟合的多项式系数: ");
        for (double coeff : coeffs) {
            System.out.println(coeff);
        }
    }
}

在这段代码中，我们首先添加了一些观测点，然后使用PolynomialCurveFitter类来进行二次多项式拟合。最后，我们得到了描述这些数据趋势的多项式系数。

4.3 优化问题求解

最后，让我们来看一个优化问题。比如说，我们需要找到一个函数的最小值点。Apache Commons Math的优化模块能够帮助我们解决这类问题。

import org.apache.commons.math3.optim.nonlinear.scalar.GoalType;
import org.apache.commons.math3.optim.nonlinear.scalar.ObjectiveFunction;
import org.apache.commons.math3.optim.nonlinear.scalar.noderiv.NelderMeadSimplex;
import org.apache.commons.math3.optim.nonlinear.scalar.noderiv.SimplexOptimizer;
import org.apache.commons.math3.optim.InitialGuess;
import org.apache.commons.math3.optim.MaxEval;

public class OptimizationProblem {
    public static void main(String[] args) {
        // 定义要优化的函数
        ObjectiveFunction objFunction = new ObjectiveFunction(x -> x[0] * Math.sin(x[0]) + x[0] * Math.cos(x[0]));

        // 使用Nelder-Mead方法进行优化
        SimplexOptimizer optimizer = new SimplexOptimizer(1e-10, 1e-30);
        NelderMeadSimplex simplex = new NelderMeadSimplex(1);
        double[] startPoint = {1.0}; // 初始猜测值
        double[] solution = optimizer.optimize(
                new MaxEval(1000),
                objFunction,
                GoalType.MINIMIZE,
                new InitialGuess(startPoint),
                simplex
        ).getPoint();

        // 打印最优解
        System.out.println("最优解在: " + solution[0]);
    }
}

在这个例子中，我们定义了一个函数，并使用Nelder-Mead方法来找到这个函数的最小值点。通过这些实战示例，我们可以看到Apache Commons Math在处理实际问题时的强大功能。这些只是它功能的一小部分，它还有很多其他强大的特性等着我们去发掘。通过合理运用这个库，我们能够有效地解决许多数学和统计问题，大大提高开发效率。

第5章：性能和实用性讨论

5.1 性能分析

Apache Commons Math是一个专注于功能的库，它的主要目标是提供广泛的数学和统计功能，而不是专注于超高性能。但这并不意味着它的性能差。实际上，对于大多数日常应用来说，它的性能是完全足够的。如果你的项目不是极端依赖于数学计算的性能，那么这个库一般不会成为瓶颈。

举个例子，如果咱们在进行一些基本的统计分析，如平均数、中位数的计算，Apache Commons Math能够快速且准确地完成任务。但如果你在做一些更高级的操作，比如大规模矩阵运算，可能就需要考虑性能了。对于这种情况，你可能需要更专业的工具，或者考虑优化你的算法。

5.2 实用性考量

接下来谈谈实用性。Apache Commons Math的一个巨大优势是它的易用性和广泛的功能范围。无论你是需要做基本的统计分析，还是要进行复杂的数值计算，这个库几乎都有相应的工具可以使用。这就大大降低了学习新工具的成本，让你能够更专注于解决业务问题。

此外，这个库的文档相当完善，社区支持也很好。这意味着如果你在使用过程中遇到问题，通常都能够找到解决方案或者得到社区的帮助。

5.3 应用场景

虽然Apache Commons Math很强大，但它并不是万能的。在某些特定应用场景中，它可能不是最佳选择。例如，在处理大规模数据集或进行高性能计算时，可能需要考虑使用更专门的工具或库。

总的来说，Apache Commons Math是一个非常实用的工具库，适用于广泛的数学和统计计算需求。它在性能和功能之间取得了很好的平衡，适合用于教育、科研以及一般的企业级应用。只要咱们清楚地了解它的优势和局限，就能在适当的场景中发挥它的最大价值。

第6章：集成与扩展

6.1 集成Apache Commons Math

集成Apache Commons Math其实挺简单的。如果你的项目用的是Maven，只需要在pom.xml文件中添加依赖就行了。这里是个例子：

<dependencies>
    <dependency>
        <groupId>org.apache.commonsgroupId>
        <artifactId>commons-math3artifactId>
        <version>3.6.1version> 
    dependency>
dependencies>

一旦添加了依赖，你就可以在项目中自由地使用Apache Commons Math的各种功能了。比如说，我们之前提到的统计分析和数学计算等。

6.2 扩展库功能

虽然Apache Commons Math已经提供了很多功能，但有时你可能需要一些特定的功能，这时就可以考虑扩展这个库。扩展库的一个常见方法是封装库中的类和方法，然后添加你需要的特定功能。

举个例子，假设你想要一个特殊的统计方法，Apache Commons Math没有直接提供。你可以创建一个新的类，继承或组合Apache Commons Math的相关类，然后添加你需要的方法。这样做既保留了原有功能，又增加了新功能。

import org.apache.commons.math3.stat.descriptive.DescriptiveStatistics;

public class ExtendedStatistics extends DescriptiveStatistics {
    // 添加一些自定义的方法
    public double getRange() {
        return getMax() - getMin();
    }

    // 你还可以添加更多功能
    // ...
}

public class App {
    public static void main(String[] args) {
        ExtendedStatistics stats = new ExtendedStatistics();
        // 使用ExtendedStatistics的方法
        // ...
    }
}

在这个例子中，我们扩展了DescriptiveStatistics类，增加了一个计算数值范围的方法。这只是扩展功能的一个简单例子，你可以根据需要添加更多复杂的功能。

6.3 与其他库的整合

最后，我们还可以探讨一下Apache Commons Math与其他库的整合。有时候，你可能需要结合使用多个库来实现项目的需求。Apache Commons Math的设计允许它很容易和其他库整合。

比如说，你可能需要将Apache Commons Math的统计功能和某个图形库结合起来，用来生成数据的可视化图表。这种情况下，你可以先用Apache Commons Math处理数据，然后用图形库生成图表。

// 假设这是某个图形库的类和方法
class ChartLibrary {
    public static void createHistogram(double[] data) {
        // 创建直方图的代码
        // ...
    }
}

public class DataVisualization {
    public static void main(String[] args) {
        DescriptiveStatistics stats = new DescriptiveStatistics();
        // 添加数据到stats
        // ...

        // 使用图形库创建直方图
        ChartLibrary.createHistogram(stats.getValues());
    }
}

在这个虚构的例子中，我们首先用Apache Commons Math进行数据分析，然后用一个假想的图形库来创建直方图。

第7章：总结

好了，经过前面七章的深入探讨，咱们现在对Apache Commons Math这个强大的Java库有了全面的了解。从基本的概念到实际应用，从最佳实践到解决常见问题，小黑和大家一起走过了这段旅程。现在，就让我们来做个总结，回顾一下这个库的核心优势。

7.1 核心优势

1. 广泛的数学和统计功能：Apache Commons Math提供了从基本的数学运算到高级统计分析的广泛功能。无论是简单的平均数计算还是复杂的优化算法，这个库都能提供强大的支持。

2. 易于使用：这个库的设计注重用户体验。它提供了清晰的API和充足的文档，使得即使是数学或编程的初学者也能相对容易地上手和使用。

3. 灵活性和扩展性：Apache Commons Math不仅易于集成到现有的Java项目中，而且还非常容易扩展。这意味着你可以根据自己的需求来定制和扩展库的功能。

4. 活跃的社区和持续的维护：作为Apache项目的一部分，这个库有着活跃的开发和维护社区。这保证了库的稳定性和持续的功能更新。

7.2 总体评价

Apache Commons Math是一个非常实用的库，适用于广泛的场景，从学术研究到商业应用。它的设计理念和强大功能使得它成为Java开发者处理数学和统计问题的优选工具。

任何工具都有其局限性。在使用Apache Commons Math时，理解它的性能特点和适用范围是非常重要的。这样，你就可以在合适的场景中发挥它的最大价值。

到此，我们关于Apache Commons Math的探索就告一段落了。希望这个库能成为你软件开发工具箱中的一颗璀璨明珠，帮助你在数学和统计计算的道路上走得更远、更稳。如果你对数学和统计充满热情，那么Apache Commons Math绝对是你不可错过的好伙伴。记住，数学不仅仅是冷冰冰的数字和公式，它还是解决问题和创造可能性的钥匙。使用Apache Commons Math，让我们一起解锁更多的可能性吧！