深度理解排序算法——快速排序
在如今所知的众多排序算法中,快速排序无疑是脱颖而出的一种高效排序算法,在众多的情景下快速排序的算法效率都是数一数二的。闲话少叙,直接开始讲解快速排序的本质。
霍尔(Hoare)法:
霍尔版本作为快速排序的最初版本,其他的版本都在霍尔版本的基础上衍生出来,因此掌握好霍尔版本的快速排序显得尤为重要。
霍尔版本排序的内容:规定一个比较数key(key常常取两端下标,本文以左端为例)和一段闭区间[left,right],先让right向前遍历至小于key的值,二者交换,再让left向前遍历至大于key的值,二者交换,循环直至left=right,将left(right)处的值与key值交换
图解:
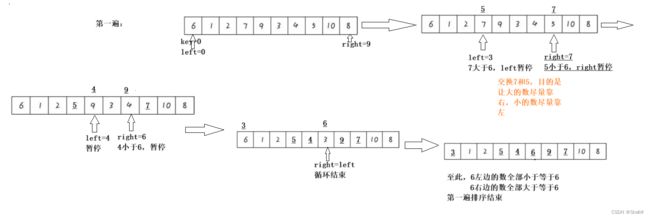
当我们把第一遍排序了解清楚后,自然会想到6左边的元素和6右边的元素要向排好序,只需要重复第一遍排序的原理,而这就可以通过递归来实现,即每一次排好序,我们都可以返回left的-1值作为左区域的末尾,+1值作为右区域的起始位置
OK,那么接下来我们就来探讨一下递归的结束条件:
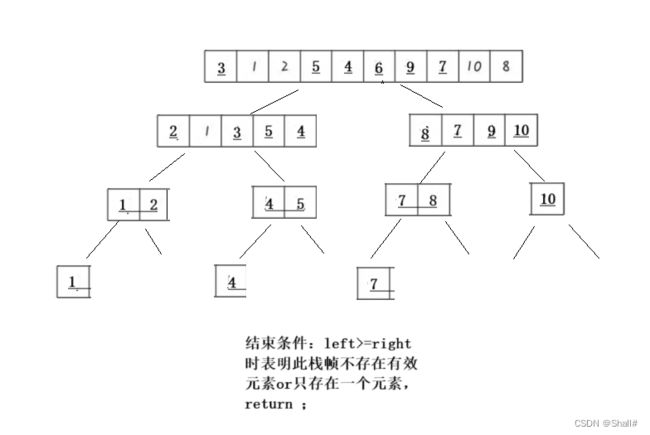
极端情况分析:*假设给定的数组最左端为0,其余元素均是正数,当right指针向前遍历的时候会由于找不到比a[key]小的元素而导致越界访问(left反之同理),故而我们必须时刻判断left和right的大小关系,避免越界,如果出现极端情况,即此次排序对数组不做任何变化。
//代码演示:
int _QuickSort(int* a,int left,int right){
int key=left;
while(left<right){
while(left<right && a[right]>=a[key])
--right;
while(left<right && a[left]<=a[key])
++left;
Swap(&a[left],&a[right]);//Swap代表交换两个值
}
Swap(a[key],a[left]);
return left;}
void QuickSort(int* a,int left,int right){
if(left>=right)
return;
int keyi=_QuickSort(a,left,right);
QuickSort(a,left,keyi-1);
QuickSort(a,keyi+1,right);}
//
挖坑法:
最初的霍尔版本在初步理解上可能难以理解,由于在逻辑上线性关系不强,因此有人衍生出了一种非常容易理解的快排版本,俗称——挖坑法
本质:假设选定最左端的数为坑,将其元素寄存到一个key临时变量中,右指针right向前遍历找到小于key的元素放入坑中,此元素原位置变为新的坑,再移动左指针找到大于key的元素放入坑中,直至left与right相遇,将key中存储的元素放入坑中,完成一次排序。剩下的就是让递归重复解决子问题了。
图解:

//代码演示:
int _QuickSort(int* a,int left,int right){
int key=a[left];
int hole=left;//坑
while(left<right){
while(left<right && a[right]<=key)
{--right;a[hole]=a[right];hole=right;}
while(left<right && a[left]>=key)
{++left;a[hole]=a[left];hole=left;}
}
a[hole]=key;
return hole;}
void QuickSort(int* a,int left,int right){
if(left<=right)
return;
int keyi=_QuickSort(a,left,right);
QuickSort(left,keyi-1);
QuickSort(keyi+1,right);}
//
双指针法:
定义两个指针分别为prev和cur,对于第一遍排序,prev=0,cur=1,指定最左端元素为比较数key。当在cur未越界的情况下,只要cur所指向的元素大于等于key所指向的元素,则cur向后移动1个单位,prev不做变化,反之交换cur与prev+1所指向的元素
图解: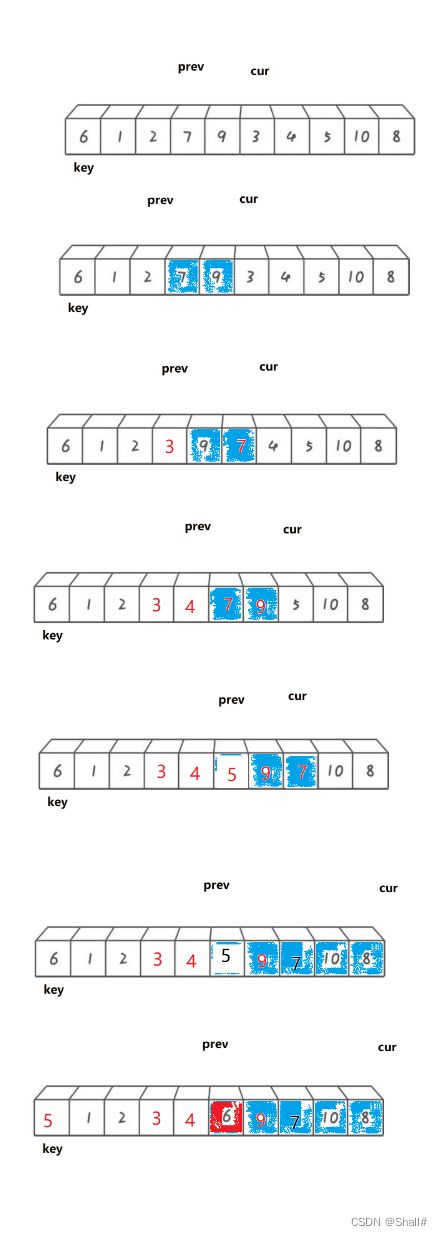
不难发现:
1、最开始prev和cur相邻的
2、当cur遇到比key的大的值以后,他们之间的值都是比key大的值
3、cur找小,找到小的以后,跟+ +prev位置的值交换相当于把大翻滚式往右边推,同时把小的换到左边
//代码演示:
int _QuickSort(int* a,int left,int right){
int key=left,prev=left;int cur=prev+1;
while(cur<right){//未越界
if(a[cur]<a[key] && ++prev!=cur)//优化算法,
Swap(&a[prev],&a[cur]); //自身交换等价于不做变化
cur++;}
Swap(&a[prev],&a[key]);
return prev;}
void QuickSort(int * a,int left,int right){
if(left>=right)
return;
int keyi=_QuickSort(a,left,right);
QuickSort(a,left,keyi-1);
QuickSort(a,keyi+1,right);}
迭代法:
顾名思义就是不采取递归的方式进行排序,通常借助栈的结构来实现
仿照递归的逻辑,先对整体进行一次排序,相当于一次入栈操作,(一次入栈两个数据,分别代表左右两端【区间】,先入的是右端,后入的是左端),再一次取出两个元素进行排序,一次排序结束后再先后压入右区域的区间和左区域的区间(必须按照这样的顺序——因为栈是先入后出的,后压入左区域的区间才会先出栈先处理)
//代码演示:
int _QuickSort(int* a,int left,int right){
int key=left;
while(left<right){
while(left<right && a[right]>=a[key])
--right;
while(left<right && a[left]<=a[key])
++left;
Swap(&a[left],&a[right]);//Swap代表交换两个值
}
Swap(a[key],a[left]);
return left;}
void QuickSort(int* a,int begin,int end){
Stack st;
StackInit(&st);
StackPush(&st,end);StackPush(&st,begin);
while(!StackEmpty(&st)){//栈为空时代表排好序了
int left=StackFront(&st);
StackPop(&st);
int right=StackFront(&st);
StackPop(&st);
int keyi=_QuickSort(a,left,right);
if(keyi+1<right)//不成立时代表单个元素或空集
{StackPush(&st,right);StackPush(&st,keyi+1);}
if(left<keyi-1)
{StackPush(&st,keyi-1);StackPush(&st,left);}
}
StackDestroy(&st);}
时间复杂度及空间复杂度:
由于递归需要建立栈帧,因此执行的时间与开辟栈帧大小密切相关,下面分析两种极端情况:
递归展开图呈现完全二叉树的形状:此时的空间复杂度即为O(logN),单排一次的时间复杂度时O(N),故而总时间复杂度为O(NlogN)
**递归展开图不存在度为2的节点:**此时的空间复杂度为O(N),那么总时间复杂度为O(N^2)
这么看的话,貌似快速排序的时间复杂度为O(N^2),看上去是一种效率很低的算法。不然,此种极端只出现在数组基本有序的情况,而基本有序的时候我们并不采用快速排序,日常中见到的大部分数据都是非常无序的,这些情况下快速排序的效率是非常高的,故而业内常常把快速排序的平均时间NlogN作为快排的时间复杂度。
但这也意味着快速排序有值得优化的地方,从逻辑图上来讲只需要让所建立的二叉树高度尽量小就可以提高计算效率,因此衍生出了一种取中值法,即不直接将left作为key,而是将left right mid三个对应值取中间值交换到最左端作比较数。
//
Over!