深度理解排序算法——归并排序
…………………………………………………………………………………
归并排序的概念:
给定一段无序数组,将数组拆分成两段,使得左右两段得数组均呈现有序状态,再借助临时数组将两段数组归并至一块呈现有序,最后拷贝回原数组即得到有序数组。
从逻辑上理解,就是一颗二叉树,将初始数组拆分成两段,再将两段拆分成四段,依次下去直至到子树节点数为1为止停止,再通过后序遍历依依对小区间不断归并。
递归方式实现:
图解:

注:
声明指针left、right、mid。 left指向数组最左端元素,right指向数组最右端元素,mid=(left+right)/2 。
显然可以看出**[left,mid]为左区域**,[mid+1,right]为右区域。
递归的结束条件是left=right返回值为true。
这里是不会出现left>right的情况的,具体证明请读者自证,当然如果你把结束条件写成left>=right也是没有问题的。
代码演示:
void _MergeSort(int* a,int* tmp,int begin,int end){
if(begin==end)
return ;
int left=begin,right=end;
int mid=(left+right)/2;
_MergeSort(a,tmp,left,mid);
_MergeSort(a,tmp,mid+1,right);
//创建begin和end增加代码可读性
int begin1=left,end1=mid;
int begin2=mid+1,end2=right;
int j=begin;
while(begin1<=end1 && begin2<=end2){
if(a[begin1]<a[begin2])
tmp[j++]=a[begin1++];
else
tmp[j++]=a[begin2++];}
while(begin1<=end1)
tmp[j++]=a[begin1++];
while(begin2<=end2)
tmp[j++]=a[begin2++];
memcpy(a+begin,tmp+begin,sizeof(int)*(end-begin+1));}
void MergeSort(int* a,int n){ //n为数组大小
int* tmp=(int*)malloc(sizeof(int)*n);
//建立临时数组,后续拷贝要用到 (中转站)
_MergeSort(a,tmp,0,n-1);
free(tmp);tmp=NULL;}
优化算法:
递归的方式最大的缺点就是建立函数栈帧非常多,存在栈溢出的风险(当然只要代码逻辑正确这种情况是较少出现的),但是建立过多的栈帧可能会导致时间代价增加
因此我们采取一种小区间优化的方式来减少大量的栈帧
只需要增加一个递归结束条件即可
对于数组大小小于10的区间采取插入排序的方式处理
if(end-begin+1<10)
{InsertSort(a,end-begin+1);//插入排序
return;}
当然这只能增加一点点的速度,并不会带来质变性提升,但对空间来说大大减少了负担
迭代方式实现:
迭代方式要比递归方式复杂多得多,原因是因为我们需要考虑很多越界情况并作出调整
我们由易入难,先举数组大小为8的特例引出雏形
图解:
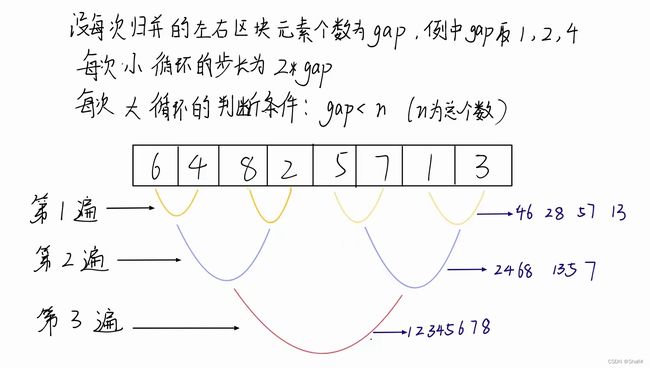
代码演示:
void MergeSortNonR(int* a,int n){
int* tmp =(int*)malloc(sizeof(int)*n);
int gap=1;//每个区域所含元素个数
while(gap<n){
int j=0;//管理tmp
for(int i=0;i<n,i+=2*gap){
int begin1=i,end1=i+gap-1;//左区域
int begin2=i+gap,end2=i+2*gap-1;//右区域
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
tmp[j++] = a[begin1++];
else
tmp[j++] = a[begin2++];
}
while (begin1 <= end1)
tmp[j++] = a[begin1++];
while (begin2 <= end2)
tmp[j++] = a[begin2++];
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
//归并一段拷贝一段
}
gap *= 2;
}
free(tmp); tmp = NULL;}
显然,上述代码块,存在非常大的局限性,它只能作用于数组大小是2^x个的数组,倘若是别的大小,那么它一定会出现指针越界的问题
下面我们来具体分析一下各种越界情况:
首先begin1是绝对不会出现越界的,因为每次的begin1初始值是i,而i必须小于n才能够进入循环体

因此我们必须对各种越界情况作出相应调整,
法一:
针对end1、begin2、end2或begin2、end2越界的情况,我们直接break,不让程序进入 while (begin1 <= end1 && begin2 <= end2) 的循环体(不对其进行归并),而针对end2越界的情况,我们只需要把end2调整为n-1即可进行归并
if(end1>=n || begin2>=n)
break;
if(end2>=n)
end2=n-1;
法二:
不通过break的方式,直接改变end1,begin2,end2的值使其不进入 while (begin1 <= end1 && begin2 <= end2)
针对第一种情况:
end1=n-1,begin2=n,end2=n-1;
针对第二种情况:
begin2=n,end2=n-1;
针对第三章情况:
end2=n-1;
**补充:对于第一第二种情况,其实只要把begin2调整至大于end2即可(begin2=1,end2=0也对)
在这种方式下,可以除了采取归并一段拷贝一段的方式,还可以采取一次gap循环结束后整体拷贝(法一会出现数据丢失,请读者自行证明)
即memcpy(a,tmp,sizeof(int)*n);
时间复杂度、空间复杂度:
平均向下建立logN个栈帧,开辟了大小为N的额外空间,故空间复杂度为O(N)
每一次归并的时间复杂度为O(N)
故总时间复杂度为O(NlogN)
可以看出归并排序是一种效率非常不错的排序算法。
文中若有错误欢迎读者指出,下期将给大家带来计数排序
觉得可以的话来个三连吧,蟹蟹!
Over!
…………………………………………………………………………………

