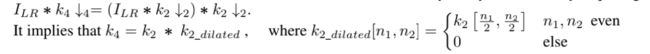KernelGAN论文详解分享
KernelGAN- Blind Super-Resolution Kernel Estimation using an Internal-GAN论文详解
论文地址:https://arxiv.org/abs/1909.06581 NeurIPS 2019 (oral)
代码下载:https://github.com/sefibk/KernelGAN
项目地址:KernelGAN
目录
论文简介
实现方法简介
G网络结构
4X下采样
G 网络loss
D网络结构
训练方法
试验结果
模糊核估计试验
SR效果对比
总结分析
参考资料
论文简介
通常超分的LR图是HR图经过Bicubic等理想的下采样核(称为SR-kernel)得到的,但真实世界的LR图像往往不是这样得到的,所以在真实世界图像上,通常的超分算法因为下采样核不想理,效果会不好。文章介绍了一种KernelGAN,是针对图像专用的内部GAN,只需要对一张LR图进行训练,经过生成器G网络,生成LR图的下采样图LR’,鉴别器D网络,无法区域LR图和LR’,二者具有相同的分布,是无监督的。其基本原理是真正的模糊核,在图像各种尺寸的图像块上具有重复性和相似性,最大相似性的模糊核,认为是当前图像的模糊核,然后通过深度学习来获取这个最可能的模糊核。训练好的G网络可以通过干净图像HR,生成和真实场景对应的LR图,和原来的输入图HR,构成LR-HR对,可以插入到现有的SR算法里使用,在真实场景SR上,可以获得不错的效果。
文章的主要贡献:
第一个估计未知SR-Kernel的深度学习方法(这是真实LR图像的真实SR的关键步骤)。KernelGAN完全不受监督,除输入图像本身外不需要任何训练数据,因此可以实现真正的SR。
当插入现有的SR算法时,KernelGAN会带来sota的Blind-SR结果。
据我们所知,这是深层线性网络的首次实际应用(迄今为止主要用于理论分析),具有明显的实际优势。
实现方法简介
主要还是使用了对抗网络思想,让下采样的图和原图具有相似的模糊程度。G网络对输入图像做下采样(2X或4X),得到一张低分辨率的LR图,然后从原图和下采样图上裁剪一个相同大小的patch,不需要像素对齐,然后分别进入D网络来进行区分,G和D网络都是全卷积网络,且D网络输出是个Map, 0表示fake,1表示Real。
具体实现时,以2X为例,是从输入图上,分别裁剪两个patch,一个给G网络,分辨率高些,代码里是64x64,这张图经过G网络之后,分辨率变为26x26,因为没有做padding,所以不是32x32,同时裁剪一个26x26的patch,是给D网络的,同时加入了少量的噪声,这样就构成了训练数据对。当然,裁剪patch时,并不是随机的,是通过构建了一个概率map,跟图像内容相关,应该是让尽量能取到边缘细节吧,G patch和D patch尽量纹理接近吧,具体没有细看。
G网络结构
G网络中没有非线性操作,全部保持线性,总共5层,7x7,5x5,3x3,其他的都是1x1,然后一个下采样,用理想的bicubic下采样核(我觉得理想的下采样,对于整数倍下采样,基本上都是接近邻近插值的,就是间隔取样的,bicubic下采样时由于会做中心对齐,如果不是中心对齐,那么bicubic和nearest是一样的,都是直接间隔采样),感受野为13x13。因为没有非线性操作,所以这些卷积层可以合成一个13x13的滤波核(如果有非线性,是不能直接转换的)。当然,好像也可以直接学这个13x13的滤波器,但根据之前CNN的一些经验,使用这种全线性结构要比直接用一个13x13的卷积要好。
通过G网络得到这个13x13滤波器的代码如下,就是通过对值全是1的输入图经过网络得到滤波器的值,输入图分辨率25x25,经过7x7卷积核之后就是19x19,经过5x5之后就是15x15,经过3x3之后,就是13x13。
# noinspection PyUnboundLocalVariable
def calc_curr_k(self):
"""given a generator network, the function calculates the kernel it is imitating"""
delta = torch.Tensor([1.]).unsqueeze(0).unsqueeze(-1).unsqueeze(-1).cuda()
for ind, w in enumerate(self.G.parameters()):
curr_k = F.conv2d(delta, w, padding=self.conf.G_kernel_size - 1) if ind == 0 else F.conv2d(curr_k, w)
self.curr_k = curr_k.squeeze().flip([0, 1])4X下采样
文章认为只要得到2X的模糊核即可,4X的模糊核可以由2X的直接得到。具体证明过程可以见网站提供的证明材料,具体实现代码如下:
def analytic_kernel(k):
"""Calculate the X4 kernel from the X2 kernel (for proof see appendix in paper)"""
k_size = k.shape[0]
# Calculate the big kernels size
big_k = np.zeros((3 * k_size - 2, 3 * k_size - 2))
# Loop over the small kernel to fill the big one
for r in range(k_size):
for c in range(k_size):
big_k[2 * r:2 * r + k_size, 2 * c:2 * c + k_size] += k[r, c] * k
# Crop the edges of the big kernel to ignore very small values and increase run time of SR
crop = k_size // 2
cropped_big_k = big_k[crop:-crop, crop:-crop]
# Normalize to 1
return cropped_big_k / cropped_big_k.sum()G 网络loss
其中前面部分是通常的GAN loss,后面的R是正则项,主要是为了限制作用,这应该是很关键的部分,具体如下:
主要是保证整体和尽可能接近1,滤波器边界的值要小,系数要稀疏,不能都一样大,这样就会过于模糊,中心像素尽可能大些。
看代码里,除了这几个loss之后,还有一个bicubic loss,就是衡量模糊核和bicubic模糊核是否一样。看了代码,lambda_centralized 和lambda_sparse和lambda_bicubic是动态调整的,如果和bicubic的模糊核相似了,权重不变了。
正则项loss的实现如下:
class DownScaleLoss(nn.Module):
""" Computes the difference between the Generator's downscaling and an ideal (bicubic) downscaling"""
def __init__(self, scale_factor):
super(DownScaleLoss, self).__init__()
self.loss = nn.MSELoss()
bicubic_k = [[0.0001373291015625, 0.0004119873046875, -0.0013275146484375, -0.0050811767578125, -0.0050811767578125, -0.0013275146484375, 0.0004119873046875, 0.0001373291015625],
[0.0004119873046875, 0.0012359619140625, -0.0039825439453125, -0.0152435302734375, -0.0152435302734375, -0.0039825439453125, 0.0012359619140625, 0.0004119873046875],
[-.0013275146484375, -0.0039825439453130, 0.0128326416015625, 0.0491180419921875, 0.0491180419921875, 0.0128326416015625, -0.0039825439453125, -0.0013275146484375],
[-.0050811767578125, -0.0152435302734375, 0.0491180419921875, 0.1880035400390630, 0.1880035400390630, 0.0491180419921875, -0.0152435302734375, -0.0050811767578125],
[-.0050811767578125, -0.0152435302734375, 0.0491180419921875, 0.1880035400390630, 0.1880035400390630, 0.0491180419921875, -0.0152435302734375, -0.0050811767578125],
[-.0013275146484380, -0.0039825439453125, 0.0128326416015625, 0.0491180419921875, 0.0491180419921875, 0.0128326416015625, -0.0039825439453125, -0.0013275146484375],
[0.0004119873046875, 0.0012359619140625, -0.0039825439453125, -0.0152435302734375, -0.0152435302734375, -0.0039825439453125, 0.0012359619140625, 0.0004119873046875],
[0.0001373291015625, 0.0004119873046875, -0.0013275146484375, -0.0050811767578125, -0.0050811767578125, -0.0013275146484375, 0.0004119873046875, 0.0001373291015625]]
self.bicubic_kernel = Variable(torch.Tensor(bicubic_k).cuda(), requires_grad=False)
self.scale_factor = scale_factor
def forward(self, g_input, g_output):
downscaled = resize_tensor_w_kernel(im_t=g_input, k=self.bicubic_kernel, sf=self.scale_factor)
# Shave the downscaled to fit g_output
return self.loss(g_output, shave_a2b(downscaled, g_output))
class SumOfWeightsLoss(nn.Module):
""" Encourages the kernel G is imitating to sum to 1 """
def __init__(self):
super(SumOfWeightsLoss, self).__init__()
self.loss = nn.L1Loss()
def forward(self, kernel):
return self.loss(torch.ones(1).to(kernel.device), torch.sum(kernel))
class CentralizedLoss(nn.Module):
""" Penalizes distance of center of mass from K's center"""
def __init__(self, k_size, scale_factor=.5):
super(CentralizedLoss, self).__init__()
self.indices = Variable(torch.arange(0., float(k_size)).cuda(), requires_grad=False)
wanted_center_of_mass = k_size // 2 + 0.5 * (int(1 / scale_factor) - k_size % 2)
self.center = Variable(torch.FloatTensor([wanted_center_of_mass, wanted_center_of_mass]).cuda(), requires_grad=False)
self.loss = nn.MSELoss()
def forward(self, kernel):
"""Return the loss over the distance of center of mass from kernel center """
r_sum, c_sum = torch.sum(kernel, dim=1).reshape(1, -1), torch.sum(kernel, dim=0).reshape(1, -1)
return self.loss(torch.stack((torch.matmul(r_sum, self.indices) / torch.sum(kernel),
torch.matmul(c_sum, self.indices) / torch.sum(kernel))), self.center)
class BoundariesLoss(nn.Module):
""" Encourages sparsity of the boundaries by penalizing non-zeros far from the center """
def __init__(self, k_size):
super(BoundariesLoss, self).__init__()
self.mask = map2tensor(create_penalty_mask(k_size, 30))
self.zero_label = Variable(torch.zeros(k_size).cuda(), requires_grad=False)
self.loss = nn.L1Loss()
def forward(self, kernel):
return self.loss(kernel * self.mask, self.zero_label)
class SparsityLoss(nn.Module):
""" Penalizes small values to encourage sparsity """
def __init__(self):
super(SparsityLoss, self).__init__()
self.power = 0.2
self.loss = nn.L1Loss()
def forward(self, kernel):
return self.loss(torch.abs(kernel) ** self.power, torch.zeros_like(kernel))D网络结构
D网络没有pooling等下采样操作,维持原来的分辨率,一个7x7的卷积核+6个1x1的卷积核,输出Map。
训练方法
由于只要一张图就可以训练得到模糊核,所以也就不需要考虑训练数据集问题。训练时迭代3000次,ADAM优化器,初始学习率0.0002,每750次学习率降10倍。
试验结果
模糊核估计试验
在合成的模糊核上进行试验,由于是合成的,所以有GT,只要和GT的结果对比,就可以知道估计的是否准确,结果如下。可以看到,和GT还是蛮接近的。
这组结果看也挺好的,还可以看到直接学13x13的卷积核效果就会差很多,足可以说明深度线性网络也是很有优势的。
同时,作者还对数据集,进行了随机模糊核退化,提供了一个数据集,和退化的方法。核心代码如下:
def gen_kernel(k_size, scale_factor, min_var, max_var, noise_level):
# Set random eigen-vals (lambdas) and angle (theta) for COV matrix
lambda_1 = min_var + np.random.rand() * (max_var - min_var)
lambda_2 = min_var + np.random.rand() * (max_var - min_var)
theta = np.random.rand() * np.pi
noise = -noise_level + np.random.rand(*k_size) * noise_level * 2
# Set COV matrix using Lambdas and Theta
LAMBDA = np.diag([lambda_1, lambda_2])
Q = np.array([[np.cos(theta), -np.sin(theta)],
[np.sin(theta), np.cos(theta)]])
SIGMA = Q @ LAMBDA @ Q.T
INV_SIGMA = np.linalg.inv(SIGMA)[None, None, :, :]
# Set expectation position (shifting kernel for aligned image)
MU = k_size // 2 + 0.5 * (scale_factor - k_size % 2)
MU = MU[None, None, :, None]
# Create meshgrid for Gaussian
[X, Y] = np.meshgrid(range(k_size[0]), range(k_size[1]))
Z = np.stack([X, Y], 2)[:, :, :, None]
# Calcualte Gaussian for every pixel of the kernel
ZZ = Z - MU
ZZ_t = ZZ.transpose(0, 1, 3, 2)
raw_kernel = np.exp(-0.5 * np.squeeze(ZZ_t @ INV_SIGMA @ ZZ)) * (1 + noise)
# shift the kernel so it will be centered
raw_kernel_centered = kernel_shift(raw_kernel, scale_factor)
# Normalize the kernel and return
kernel = raw_kernel_centered / np.sum(raw_kernel_centered)
return kernelSR效果对比
为了对比,作者做了4类算法进行分析对比。
- 理想核下采样SOTA SR算法,就是直接用bicubic下采样训练的SR网络
- NTIRE2018 盲超分的效果较好的算法
- 模糊核估计+SR方法,就是先估计出模糊核,然后再通过模糊核得到HR-LR数据对进行训练
- GT模糊核+SR方法,和3类似,只是模糊核已知,可以认为是3的上限。
结果如下,可以看到模糊核估计+SR的方法,效果是不错的,当然和GT模糊核对比,还是有些差异的,NTIRE2018 第一名在4X的效果上也不错,估计可能是有噪声估计的原因,或者加入了噪声退化模型,文章只估计模糊核,对噪声模型模考虑,可能还是有些影响的。
总结分析
从结果来看,模糊核通过这种方法,估计的还比较准确,我也试验了不少图片,如果是比较清晰的图像,估计出来的模糊核bicubic很接近,但模糊图像,估计出来的模糊核就和bicubic差异很大,还有些时各项异性的模糊核,应该说是比较好的。
而作者说的最好的SR效果是KernelGAN+ZSSR[1],我想主要是因为这两者都是image-specifific,所以效果比其他SOTA效果要好,因为其他SOTA算法不是只处理一张图。
对于SR来说,用模糊核估计并不意味效果一定就好了,首先,这里只考虑模糊核,并没有考虑其他噪声模型和JPEG压缩的影响(当然某些场景是没有JPEG压缩损失的),考虑的不够全面;其次,如果没有估计模糊核,但可以随机造模糊核,然后让网络去学,网络较大时,应该可以学会,就像Real-ESRGAN[2]那样。
参考资料:
[1] “Zero-Shot” Super-Resolution using Deep Internal Learning
[2] Real-ESRGAN: Training Real-World Blind Super-Resolution with Pure Synthetic Data