什么是高/低方差、高/低偏差、(推荐阅读)

概念

偏差： 描述的是预测值（估计值）的期望与真实值之间的差距。偏差越大，越偏离真实数据集。

（Ps:假设靶心是最适合给定数据的模型，离靶心越远，我们的预测就越糟糕）

方差： 描述的是预测值的变化范围，离散程度，也就是离其期望值的距离。方差越大，预测结果数据的分布越散。

基于偏差的误差： 所谓基于偏差的误差是我们模型预期的预测与我们将要预测的真实值之间的差值。偏差是用来衡量我们的模型的预测同真实值的差异。

基于方差的误差： 基于方差的误差描述了一个模型对给定的数据进行预测的可变性。比如，当你多次重复构建完整模型的进程时，方差是，在预测模型的不同关系间变化的多少。

接下来，我们把四张图合并起来：

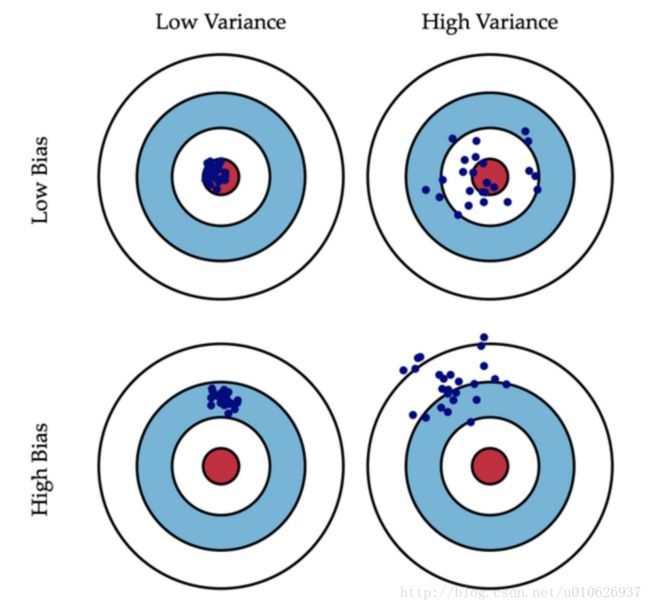
解释：
左上：低偏差，低方差。表现出来就是，预测结果准确率很高，并且模型比较健壮（稳定），预测结果高度集中。

右上：低偏差，高方差。表现出来就是，预测结果准确率较高，并且模型不稳定，预测结果比较发散。

左下：高偏差，低方差。表现出来就是，预测结果准确率较低，但是模型稳定，预测结果比较集中。

右下：高偏差，高方差。表现出来就是，预测结果准确率较低，模型也不稳定，预测结果比较发散。

举个例子，让你二次开窍

想象你开着一架黑鹰直升机，得到命令攻击地面上一只敌军部队，于是你连打数十梭子，结果有一下几种情况:

1.子弹基本上都打在队伍经过的一棵树上了，连在那棵树旁边等兔子的人都毫发无损，这就是方差小（子弹打得很集中），偏差大（跟目的相距甚远）。

2.子弹打在了树上，石头上，树旁边等兔子的人身上，花花草草也都中弹，但是敌军安然无恙，这就是方差大（子弹到处都是），偏差大（跟目的相距甚远）。

3.子弹打死了一部分敌军，但是也打偏了些打到花花草草了，这就是方差大（子弹不集中），偏差小（已经在目标周围了）。

4.子弹一颗没浪费，每一颗都打死一个敌军，跟抗战剧里的八路军一样，这就是方差小（子弹全部都集中在一个位置），偏差小（子弹集中的位置正是它应该射向的位置）。

方差，是形容数据分散程度的，算是“无监督的”，客观的指标，偏差，形容数据跟我们期望的中心差得有多远，算是“有监督的”，有人的知识参与的指标。

三次理解

偏差（bias）:对象是单个模型， 期望输出与真实标记的差别。

方差（Variance）：对象是多个模型,表示多个模型差异程度。

以上图为例：
1. 左上的模型偏差最大，右下的模型偏差最小；
2. 左上的模型方差最小，右下的模型方差最大

为了理解第二点，可以看下图。蓝色和绿色分别是同一个训练集上采样得到的两个训练子集，由于采取了复杂的算法去拟合，两个模型差异很大。如果是拿直线拟合的话，显然差异不会这么大。

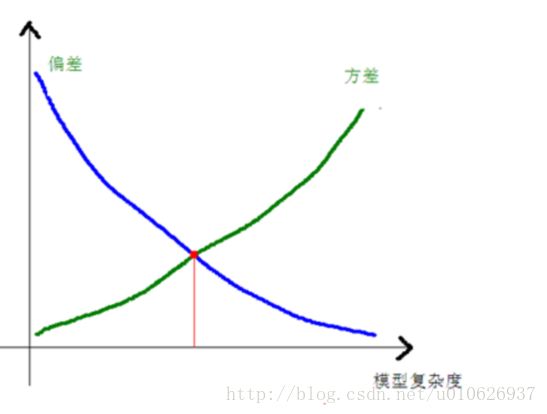
一般来说，偏差、方差和模型的复杂度之间的关系如下图所示：

越复杂的模型偏差越小，而方差越大。

我们用一个参数少的，简单的模型进行预测，会得到低方差，高偏差，通常会出现欠拟合。

而我们用一个参数多的，复杂的模型进行预测，会得到高方差，低偏差，通常出现过拟合。

实际中，我们需要找到偏差和方差都较小的点。从上图可以看出在偏差和方差都较小的点处，total Error是最少的。

XGBOOST中，我们选择尽可能多的树，尽可能深的层，来减少模型的偏差；
通过cross-validation，通过在验证集上校验，通过正则化，来减少模型的方差从而获得较低的泛化误差。

拓展

数学上的定义：

我们定义我们要预测的变量为Y，协变量为X，我们假设有Y=f(X)+ϵ，其中误差项服从均值为0的正态分布.
我们用线性回归或者别的模型来估计f(X) 为.其中，对x来说，误差为：

将上式展开，然后用偏差和方差表述：

注意：最后一项为噪声，是无法通过模型降低的。

通过上面的式子也可看出，要使得误差低，就要使得偏差和方差都要低。

参考文献

为了帮助理解，尤其是拓展部分，可以参考一下参考文献

1. 理解机器学习中的偏差与方差
2. Understanding the Bias-Variance Tradeoff

这么聪明的你，一定理解了吧！加油！

《完》

所谓的不平凡就是平凡的N次幂。
					----By Ada