机器学习基础整理(第2章) - 模式分类
文章目录
- 什么是模式识别/分类器?
- 基础模型 - 模式分类器
- 监督和非监督分类器
- 贝叶斯决策规则
-
- 最小误差 (Minimum Error)
- 最小风险 (Minimum Risk)
- 最小损失和最小风险的关系
- Neyman-Pearson决策规则
- 判别函数 (Discriminant Function)
-
- 线性判别函数 (Linear Discriminant Functions)
-
- 线性机
- 分段线性判别函数 (Piecewise Linear Discriminant Functions)
什么是模式识别/分类器?
我们理所当然地认为我们能够在我们的世界中走动并认识到:
汽车,人类,动物,一般对象,尽管它们的形式和存在多种多样。
在这些任务中,什么特征帮助我们识别?
在模式识别中,
- 我们研究如何设计能够辨认或分类"事物"的机器。
- 我们研究能描述"事物"的特征的统计。
- 我们研究如何衡量模式识别系统的性能 以及 选择表现好的系统。
基础模型 - 模式分类器

模式 (pattern) 是一组 能代表一个 p p p 维向量的 数字或值,
x = [ x 1 , x 2 , . . . , x p ] t x=[x_1, x_2, ..., x_p]^t x=[x1,x2,...,xp]t
其中 t t t (有时候也可以是 T T T ) 代表了向量转置。
模式的例子:
- 图片中的像素
- 股票在股票市场上的收盘价
- 语音信号的录音
- 天气变量的测量
- 一组关于房产的测量值
- 一组关于人的行为和生活方式的测量
- 等等
假设存在 C C C 种类别,其被表示为:
ω 1 , . . . , ω C \omega_1, ..., \omega_C ω1,...,ωC
存在一个变量 z z z, 其代表一个模式 x x x 属于 哪个类别 ω i \omega_i ωi,也就是:
若 z = i z=i z=i,则模式 x x x 属于 类别 ω i \omega_i ωi, i ∈ { 1 , . . . , C } i \in \{1, ..., C\} i∈{1,...,C}
现在我们的问题就是如何设计模式分类器。
设计一个模式分类器意味着,我们需要指定分类器模型参数,以及确保其指定模式的响应 (response) 是最优的。
设计流程: 我们拥有一组已知类别的模式 { ( x i , z i ) } \{(x_i, z_i)\} {(xi,zi)},其被称为训练或设计集,被用来设计分类器。评估以及设置最佳操作参数 (optimal operating parameters) 。
一旦我们拥有已设计好的分类器,我们就可以估计 未知模式 的类别所属。
通常,我们假设用于 训练的样本 来自与 测试样本 和 操作样本 (operational samples) 相同的概率分布。
对于一个分类器,我们得知:
- 表示模式 (representation pattern) 是我们从传感器中获得的原始数据 (raw data),如,图片或视频像素,股票价格等。
- 特征模式 (feature pattern) 是一小组 从一些 转换 获取的变量,如根据特征选择或提取。
- 训练好的分类器使用特征模式对其输入处所呈现的模式做出决定。
此外,还有一些需要注意的:
- 我们要解决的问题: 给定一组 已知类别模式 的训练集,我们寻求设计一个对 预期操作条件 最佳的分类器。
- 给定的 训练模式集 (training patterns) 是有限的。
- 分类器模型不能过于复杂,它不能拥有太多参数,否则可能会导致过拟合。
- 在 训练集 上达到 最优性能 并不重要。
- 达到最优的泛化性能非常重要。( 这代表的是 真实操作条件的数据 的预期性能 - 指的是 能提取出训练集 的无限集 infinite set)
监督和非监督分类器
主要有两种类别的分类器:
- 监督型: 分类器设计流程拥有一组带标签 (类别) 的数据样本,这就是示例或训练集。
- 非监督型: 给定的数据是没被标注的,我们要从 能区分各组的数据和特征中去寻找组别。
- 半监督型: 标注的和未标注的数据都被用于训练。
使用尽可能简单的模型来描述系统的原则在 “Occan’s razor” 中得到了体现,即对那些不必要复杂的事物进行更简单的解释。该原理是非常流行的稀疏表示方法 (sparse representation) 的基础。
贝叶斯决策规则
最小误差 (Minimum Error)
这种分类方法 (也被称为判别 discrimination) 假设了我们完全了解每个类别的概率密度函数。
使 C C C个类别拥有已知的先验概率 (priori probabilities), P ( ω 1 ) , . . . , P ( ω C ) P(\omega_1), ..., P(\omega_C) P(ω1),...,P(ωC)。我们使用 测量向量 (measurement vector) x x x将 x x x 分配给 C C C 个类别之一。
制定一个能通过 使 让给定观测 x x x 分配 类别 ω j \omega_j ωj 时 在 ω 1 , . . . , ω C \omega_1, ..., \omega_C ω1,...,ωC 中 拥有最高概率 (如, P ( ω j ∣ x ) P(\omega_j|x) P(ωj∣x),后验概率 posterior probability),接着将 x x x 分配给 类别 ω j \omega_j ωj 的决策规则。

我们可以使用贝叶斯定理根据 先验概率 和 类条件密度函数 (class-conditional density functions) p ( x ∣ ω i ) p(x|\omega_i) p(x∣ωi) 来表达后验概率 P ( ω j ∣ x ) P(\omega_j|x) P(ωj∣x)

注: 根据统计或者经验得到的概率值,被称为先验概率。而事情已经发生,要得到这件事情发生的原因是由某个因素引起的可能性大小则被称为后验经验,也可以说,通过贝叶斯定理和先验概率计算出来的结果就是后验概率。
根据类条件密度,我们可以将决策规则写为,若要将 x x x 分配给 ω j \omega_j ωj,则:
p ( x ∣ ω j ) P ( ω j ) > p ( x ∣ ω k ) P ( ω k ) , k = 1 , . . . , C , k ≠ j p(x|\omega_j)P(\omega_j) \gt p(x|\omega_k)P(\omega_k), k = 1, ..., C, k \ne j p(x∣ωj)P(ωj)>p(x∣ωk)P(ωk),k=1,...,C,k=j
这就是贝叶斯最小误差规则 (Bayes’ rule for minimum error)。
注: 贝叶斯误差是在给定特征记得情况下,假定数据无限且准确,依靠统计所能得到的最小误差。(假设真实世界中90%长头发的人为女性,10%为男性 (这是已知的真实分布);此时已知一个人头发长,预测该同学性别。由于只能预测男/女。此时即使你知道真实分布,预测为女,也会有10%的误差。这就是贝叶斯误差。) 实际上,贝叶斯误差难以求得,该指标更多在学术领域中更有意义。
在二分类的情况下,我们能将贝叶斯最小误差规则写成 似然比 (likelihood ratio, L r ( x ) L_r(x) Lr(x)) 的形式 (对于, x ∈ c l a s s ω 1 x \in class \omega_1 x∈classω1):
L r ( x ) = p ( x ∣ ω 1 ) p ( x ∣ ω 2 ) > P ( ω 2 ) P ( ω 1 ) , L_r(x) = \frac{p(x|\omega_1)}{p(x|\omega_2)} \gt \frac{P(\omega_2)}{P(\omega_1)}, Lr(x)=p(x∣ω2)p(x∣ω1)>P(ω1)P(ω2),
举个例子,有一个二分类的判别问题,其中类别 ω 1 \omega_1 ω1 其符合正态分布 p ( x ∣ ω 1 ) = N ( x ∣ 0 , 1 ) p(x|\omega_1) = N(x | 0, 1) p(x∣ω1)=N(x∣0,1),而 类别 ω 2 \omega_2 ω2 则符合正态混合分布 p ( x ∣ ω 2 ) = 0.6 N ( x ∣ 1 , 1 ) + 0.4 N ( x ∣ − 1 , 2 ) p(x|\omega_2) = 0.6N(x|1, 1) + 0.4N(x|-1, 2) p(x∣ω2)=0.6N(x∣1,1)+0.4N(x∣−1,2)
p ( x ∣ ω i ) p ( ω i ) , i = 1 , 2 p(x|\omega_i)p(\omega_i), i=1,2 p(x∣ωi)p(ωi),i=1,2 并且 P ( ω 1 ) = P ( ω 2 ) = 0.5 P(\omega_1) = P(\omega_2) = 0.5 P(ω1)=P(ω2)=0.5 的图像如下:

下图 是 似然比 L r ( x ) L_r(x) Lr(x) 以及 阈值 P ( ω 2 ) / P ( ω 1 ) P(\omega_2)/P(\omega_1) P(ω2)/P(ω1)
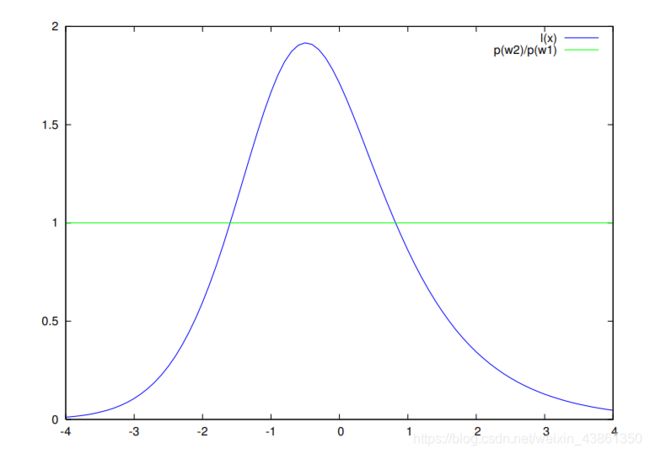
根据图像,若 L r ( x ) > P ( ω 2 ) P ( ω 1 ) L_r(x) \gt \frac{P(\omega_2)}{P(\omega_1)} Lr(x)>P(ω1)P(ω2),则观测到的样本会被分类为 ω 1 \omega_1 ω1。
最小风险 (Minimum Risk)
这个决策规则最小化预期的损失或风险。
定义一个损失矩阵, ∧ \land ∧,其中的元素为:
λ j i = \lambda_{ji} = λji= 当 x ∈ ω j x \in \omega_j x∈ωj 的时候,将模式 x x x 分配给 ω i \omega_i ωi 的成本。
分配一个模式 x x x 到 类别 ω i \omega_i ωi 的 条件风险 (conditional risk) 被定义为:

决策区域 (decision region) Ω i \Omega_i Ωi的平均风险为:

通过将与 所有类别相关的风险 相加能得到 总体预期成本或风险:

若区域 Ω i \Omega_i Ωi 被选择时,风险最小且使得:

则我们可以称 x ∈ Ω i x \in \Omega_i x∈Ωi
贝叶斯风险, r ∗ r^* r∗,即是:

对于一个二分类问题,我们可以将 条件风险 写为:

最小风险决策规则能在 l 1 ( x ) < l 2 ( x ) l_1(x) \lt l_2(x) l1(x)<l2(x) 的情况下,简单地确定 ω 1 \omega_1 ω1 就是期望的类别。
这也可以用后验概率来表示:
当 ( λ 11 − λ 12 ) P ( ω 1 ∣ x ) < ( λ 22 − λ 21 ) P ( ω 2 ∣ x ) (\lambda_{11}-\lambda_{12})P(\omega_1|x) \lt (\lambda_{22}-\lambda_{21})P(\omega_2|x) (λ11−λ12)P(ω1∣x)<(λ22−λ21)P(ω2∣x) 的情况下,我们能确定 ω 1 \omega_1 ω1
也可以用先验概率和条件密度来表示:
当 ( λ 11 − λ 12 ) p ( x ∣ ω 1 ) P ( ω 1 ) < ( λ 22 − λ 21 ) p ( x ∣ ω 2 ) P ( ω 2 ) (\lambda_{11}-\lambda_{12})p(x|\omega_1)P(\omega_1) \lt (\lambda_{22}-\lambda_{21})p(x|\omega_2)P(\omega_2) (λ11−λ12)p(x∣ω1)P(ω1)<(λ22−λ21)p(x∣ω2)P(ω2) 的情况下,我们能确定 ω 1 \omega_1 ω1
最小损失和最小风险的关系
若我们考虑一种特殊情况 同等成本 (对称 或 0-1) 损失矩阵, ∧ \land ∧,即:

将此条件替换为最小风险贝叶斯决策规则,则得出对于 k = 1 , . . . , C k = 1, ..., C k=1,...,C:
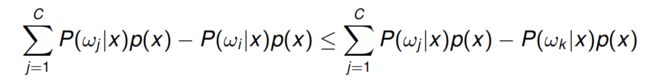
这个式子能被简化为,当 x ∈ c l a s s ω i x \in class \omega_i x∈classωi 时:
p ( x ∣ ω i ) p ( ω i ) ≥ p ( x ∣ ω k ) p ( ω k ) , k = 1 , . . . , C p(x|\omega_i)p(\omega_i) \ge p(x|\omega_k)p(\omega_k), k = 1, ..., C p(x∣ωi)p(ωi)≥p(x∣ωk)p(ωk),k=1,...,C
这就和最小误差贝叶斯规则一样了。
这种情况下1-0损失矩阵 (zero-one loss matrix) 的相关风险是:
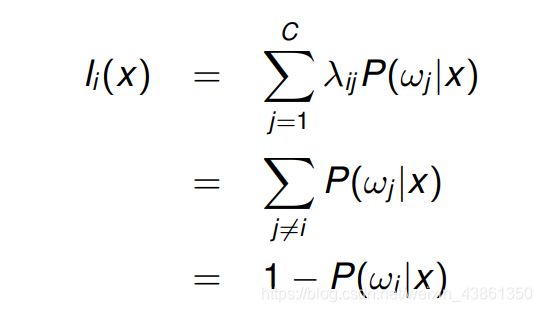
Neyman-Pearson决策规则
对于二分类问题,这是贝叶斯决策规则的替代方法。
在二分类问题中,被定义了两种类型的误差:
- 类型一 (Type I): 将一个类别 ω 1 \omega_1 ω1 的模式分类为属于 类别 ω 2 \omega_2 ω2 并具有相关的错误概率

- 类型二 (Type II): 将一个类别 ω 2 \omega_2 ω2 的模式分类为属于 类别 ω 1 \omega_1 ω1 并具有相关的错误概率

Neyman-Pearson 决策规则目的就是在 ϵ 2 \epsilon_2 ϵ2 等于 常数 ϵ 0 \epsilon_0 ϵ0 的情况下,最小化 ϵ 1 \epsilon_1 ϵ1。

该决策规则适用于信号处理,例如 雷达信号检测等 双向检测问题 (two-way detection problem)。
若我们将 类别 ω 1 \omega_1 ω1 视作 阳性类 (positive class),而将 ω 2 \omega_2 ω2 视为 阴性类 (negative class),我们有:
- Type I 误差概率: 被称为 假阴性率 (false negative rate),也就是阳性样本被错误分配到 阴性类别 的比例。

- Type II 误差概率: 被称为 假阳性率 (false positive rate),也就是阴性样本被错误分配到 阳性类别 的比例。

Type II 误差 也被称为 误报 (false alarm)。
这一决策规则 最小化 目标函数:

其中, μ \mu μ 是拉格朗日乘数。
若我们选择 Ω 1 \Omega_1 Ω1 使得 被积函数(integrand) 为负,则目标函数被最小化了。
即是,若 μ p ( x ∣ ω 2 ) − p ( x ∣ ω 1 ) < 0 \mu p(x|\omega_2) - p(x|\omega_1) \lt 0 μp(x∣ω2)−p(x∣ω1)<0,则 x ∈ Ω 1 x\in\Omega_1 x∈Ω1
这可以被写为,若 p ( x ∣ ω 1 ) p ( x ∣ ω 2 ) > μ \frac{p(x|\omega_1)}{p(x|\omega_2)} \gt \mu p(x∣ω2)p(x∣ω1)>μ,则 x ∈ Ω 1 x\in\Omega_1 x∈Ω1
通过使得下面式子成立来选择 μ \mu μ

其中, ϵ 0 \epsilon_0 ϵ0通常应用 数值解 被找到。
决策规则的性能被以 能画出 正阳率 (true positive - ( 1 − ϵ 1 ) (1 - \epsilon_1) (1−ϵ1)) 和 假阳率 (false positive - ϵ 2 \epsilon_2 ϵ2) 的接收器操作特征 (receiver operating characteristic - ROC) 曲线
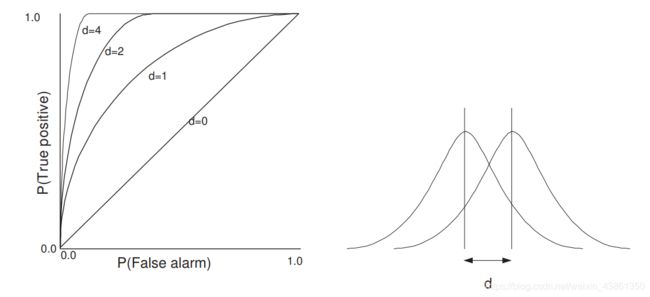
两个 单变量正态分布 (univariate normal distribution) 和 不同 d d d 值的接收器操作特征 (ROC), d = ∣ µ 1 − µ 2 ∣ d = |µ_1 − µ_2| d=∣µ1−µ2∣, µ 1 µ_1 µ1 和 µ 2 µ_2 µ2 是分布的平均值。
判别函数 (Discriminant Function)
贝叶斯决策规则要求要有 通常在实践中并不可用的 先验类概率知识 (knowledge of prior class probabilities) 以及 类条件密度 (class conditional densities),这些必须从数据中估计。
所引入的技术类别 不对 p ( x ∣ ω i ) p(x|ω_i) p(x∣ωi) 做任何假设,而是假设一种 判别函数 的形式。
判别函数是引出分类规则 (classfication rule) 的特征向量 x x x 函数。
在一个二分类问题中,一个判别函数 h ( x ) h(x) h(x) 对于一个常数 k k k 满足:

判别函数并不唯一,若 f ( . ) f(.) f(.) 是一个 单调函数 ( 在定义域中单调递增或递减 ),则:

其中 k ‘ = f ( k ) k^‘=f(k) k‘=f(k),其和 h ( x ) h(x) h(x) 给出一样的决策。
对于 C C C 个类别的分类问题,我们定义 C C C 个判别函数,若 g i ( x ) g_i(x) gi(x) 成立则:
g i ( x ) > g j ( x ) ⇒ x ∈ ω i , j = 1 , . . . , C ; j ≠ i g_i(x) \gt g_j(x) \Rightarrow x \in \omega_i, j = 1, ..., C; j \ne i gi(x)>gj(x)⇒x∈ωi,j=1,...,C;j=i
这意味着一个特征向量被分配到了有最大判别 (largest discriminant) 的类。
判别技术依靠 被指定的函数形式,而非潜在的分布。
函数的参数在训练过程中被改变调整。
线性判别函数 (Linear Discriminant Functions)
线性判别函数是 测量(或特征)向量 x = [ x 1 , x 2 , . . . , x p ] t x = [x_1, x_2, ..., x_p]^t x=[x1,x2,...,xp]t 中元素的线性组合,使得:
g ( x ) = ω t x + ω 0 = ∑ i = 1 p ω i x i + ω 0 g(x) = \omega^tx+\omega_0=\sum_{i=1}^p\omega_ix_i+\omega_0 g(x)=ωtx+ω0=i=1∑pωixi+ω0
其中我们需要指定 权重向量 (weight vector) ω \omega ω 以及 阈值权重 (threshold weight) ω 0 \omega_0 ω0。
该式子描述一个 超平面 (hyperplane),其单位法向 (unit normal) 在 ω \omega ω 方向上,从原点的垂直距离 (perpendicular distance) 为 ∣ ω 0 ∣ / ∣ ω ∣ |\omega_0|/|\omega| ∣ω0∣/∣ω∣
下图表明了线性判别函数的几何

模式 x x x 的 判别函数的值 是与 超平面 的垂直距离。
线性机
使用线性判别函数的分类器一般被称为 线性机 (linear machines)。
最小距离分类器 (minimum-distance classifier) 是一个例子。其使用 最近邻点 (nearest-neighbour) 决策规则。
使分类器的原型点 (prototype points) 表示为 p 1 , . . . , p C p_1, ..., p_C p1,...,pC,每一个点代表一个分类 ω i \omega_i ωi,最小距离分类器将 x x x 根据 最近点 p i p_i pi 分配给 类别 ω i \omega_i ωi。
∣ ∣ x − p i ∣ ∣ 2 = x t x − 2 x t p i + p i t p i ||x - p_i||^2 = x^tx - 2x^tp_i + p_i^tp_i ∣∣x−pi∣∣2=xtx−2xtpi+pitpi
分配到 x x x 的类为:
ω i = m a x i ( x t p − 1 2 p i t p i ) \omega_i = max_i(x^tp-\frac{1}{2}p_i^tp_i) ωi=maxi(xtp−21pitpi)
我们可以将这个分配 联系到 线性判别函数中:
g ( x ) = ω i t x + ω i 0 g(x) = \omega^t_ix+\omega_{i0} g(x)=ωitx+ωi0
其中:
ω i = p i \omega_i = p_i ωi=pi
ω i 0 = − 1 2 ∣ ∣ p i ∣ ∣ 2 \omega_{i0} = -\frac{1}{2}||p_i||^2 ωi0=−21∣∣pi∣∣2
这表明了其确实是一个线性机。
可以选择原型点作为每个类的均值,来得到一个类均值分类器 (class mean classifier)。
每个边界 (boundary) 是连接 相邻区域 的原型点的线的垂直平分线 (perpendicular bisector)。也要注意到,线性机的决策区域 (decision regions) 总是凸函数 (convex)。
下图是 最小距离分类器的决策区域。
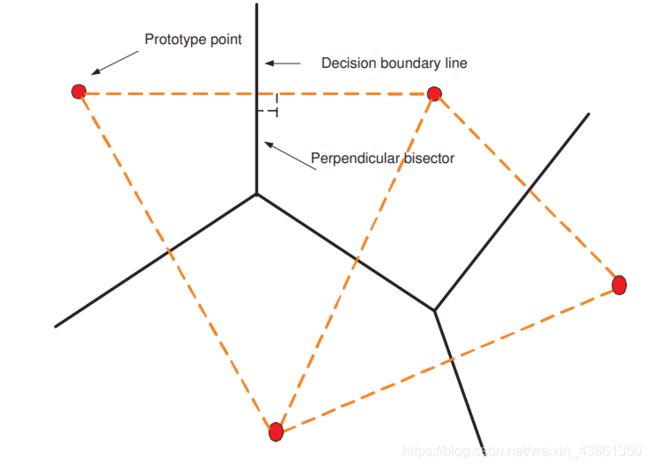
分段线性判别函数 (Piecewise Linear Discriminant Functions)
线性机拥有简单形式,但其也有限制,也就是其无法分离决策区域必须是非凸 (non-convex) 的情况。
下面的例子展示了线性判别式无法分离的二分类问题,其需要分段线性判别函数。

我们能通过使用 分段线性判别函数 来推广 最小距离分类器 以解决前面的 二分类问题。对于每个类别,我们允许多于一个原型点的存在。
假设在类别 ω i \omega_i ωi 有 n i n_i ni 个原型点, p i 1 , . . . , p i n i , i = 1 , . . . , C p_i^1, ..., p_i^{n_i}, i=1, ..., C pi1,...,pini,i=1,...,C
将模式 x x x 分配给 类别 ω i \omega_i ωi 的 判别函数 被定义为:

其中 g i j g_i^j gij 是一个 线性辅助判别函数 (linear subsidiary discriminant function),被定义为:
g i j ( x ) = x t p i j − 1 2 p i j t , j = 1 , . . . , n i ; i = 1 , . . . , C g_i^j(x) = x^tp_i^j -\frac{1}{2}p_i^{j^t}, j = 1, ..., n_i; i =1, ..., C gij(x)=xtpij−21pijt,j=1,...,ni;i=1,...,C
