《人工智能导论》 第5章 搜索求解策略

搜索求解策略

搜索的概念

搜索的基本问题与主要过程

• 搜索中需要解决的基本问题：
  • 是否一定能找到一个解。
  • 找到的解是否是最佳解。
  • 时间与空间复杂性如何。
  • 是否终止运行或是否会陷入一个死循环
• 搜索的主要过程
  1. 从初始或目的状态出发，并将它作为当前状态。
  2. 扫描操作算子集，将适用当前状态的一些操作算子作用在其上而得到新的状态，并建立指向其父结点的指针。
  3. 检查所生成的新状态是否满足结束状态，如果满足，则得到解，并可沿着有关指针从结束状态反向到达开始状态，给出一解答路径；否则，将新状态作为当前状态，返回第②步再进行搜索。

搜索策略

• 数据驱动：从初始状态出发的正向搜索。
• 目的驱动：从目的状态出发的逆向搜索。
• 盲目搜索：在不具有对特定问题的 任何有关信息的条件下，按固定的步骤（依次或随机调用操作算子）进行的搜索。
• 启发式搜索：考虑特定问题领域可应用的知识，动态地确定调用操作算子的步骤，优先选择较适合的操作算子，尽量减少不必要的搜索，以求 尽快地到达结束状态。

状态空间的搜索策略

状态空间表示法

状态空间表示法用状态变量和操作符号来表示系统或问题的符号体系。状态空间可以用一个四元组表示：
$$(S,O,S_0,G)$$
其中 $S$ 是状态集合。 $O$ 是操作算子的集合。 $S_0$ 是包含问题的初始状态，是 $S$ 的非空子集。 $G$ 是包含问题的目的状态若干具体状态或满足某些性质的路径信息描述。

• 状态：表示系统状态、事实等叙述型知识的一组变量或数组。
  $$Q=[q_1,q_2,\cdots ,q_n{]}^T$$

• 操作：表示引起状态变化的过程型知识的一组关系或函数。
  $$F=\{f_1,f_2,\cdots ,f_n\}$$

• 求解路径：从$S_0$节点到$G$节点的路径。

• 状态空间的一个解：一个有限的操作算子序列。
  $$S_0\stackrel{O_1}{⟶}{S}_1\stackrel{O_2}{⟶}{S}_2\stackrel{O_3}{⟶}\cdots \stackrel{O_k}{⟶}G$$
  其中 $O_1\cdot \cdot \cdot O_K$ 是状态空间的一个解。

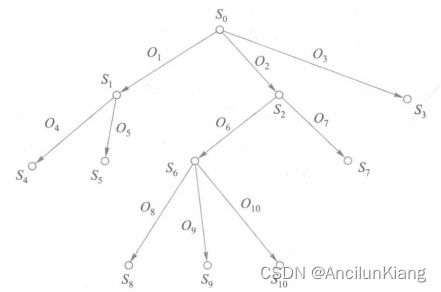
状态空间的图描述

状态空间可用有向图来描述，图的结点表示问题的状态，图的弧表示状态之间的关系，就是求解问题的步骤。初始状态对应于实际问题的已知信息，是图中的根结点。问题的状态空间描述中，寻找从一种状态转换为另一种状态的某个操作算子序列就等价于在一个图中寻找某一路径。

盲目的图搜索策略

回溯策略

从初始状态出发，不停地、试探性地寻找路径， 直到它到达目的或“不可解结点” ，即“死胡同” 为止。回溯策略是遇到不可解结点就回溯到路径中最近的 父结点上，查看该结点是否还有其他的子结点未被 扩展。若有，则沿这些子结点继续搜索；如果找到 目标，就成功退出搜索，返回解题路径。

回溯搜索的算法用三张表来保存状态空间中的不同性质节点：

• 路径状态表/PS表（path states）：保存当前搜索路径上的状态。如果找到了目的，PS就是解路径上的状态有序集。
• 新的路径状态表/NPS表（new path states）：新的路径状态表。它包含了等待搜索的状态，其后裔状态还未被搜索到，即未被生成扩展 。
• 不可解状态表/NSS表（no solvable states）：不可解状态集，列出了找不到解题路径的状态。如果在搜索中扩展出的状态是它的元素，则可立即将之排除，不必沿该状态继续搜索。

搜索算法的回溯思想：

1. 用未处理状态表（NPS）使算法能返回（回溯）到其中任一状态。
2. 用一张“死胡同”状态表（NSS）来避免算法重新搜索无解的路径。
3. 在PS 表中记录当前搜索路径的状态，当满足目的时可以将它作为结果返回。
4. 为避免陷入死循环必须对新生成的子状态进行检查， 看它是否在该三张表中 。

宽度优先搜索策略

在实际宽度优先搜索时，为了保存状态空间搜索的轨迹，用到了两个表：

• OPEN表：类似NPS表，记录了已生成但其子状态待考察的节点。宽度优先搜索算法中OPEN表是队列结构，其中状态的排列次序就是搜索的次序。
• CLOSED表：相当于PS表和NSS表的合并，记录了已被生成扩展过的状态。

宽度优先搜索过程：

1. 把起始节点放到OPEN表中。
2. 如果OPEN是个空表，则没有解， 失败退出，否则继续。
3. 把第一个节点（节点 n）从OPEN 表移出，并把它放入CLOSED扩展节点表中。
4. 考察节点n是否为目标节点。如果是，则求得了问题的解，退出。
5. 如果节点n不可扩展，则转第 2 步。
6. 把 n 的所有子节点放到OPEN表的尾部，并为其配置指向父节点的指针，然后转第 2 步。

宽度优先算法的改进：

由原来从OPEN表取出后放入CLOSE表前访问改为扩展其子节点时直接访问其子节点，可以避免访问目标节点的左侧同级节点。

1. 把起始节点放到OPEN表中。
2. 考察该初始节点是否为目标节点。如果是，则求得了问题的解，退出。
3. 如果OPEN是个空表，则没有解， 失败退出，否则继续。
4. 把第一个节点（节点 n）从OPEN 表移出，并把它放入CLOSED扩展节点表中。
5. 如果节点n不可扩展，则转第 2 步。
6. 考察节点n的子节点是否为目标节点。如果是，则求得了问题的解，退出。把 n 的所有子节点放到OPEN表的尾部，并为其配置指向父节点的指针，然后转第 2 步。

深度优先搜索策略

在实际深度优先搜索时，也用到了OPEN表和CLOSED表，不同的是，深度优先搜索算法中OPEN表是堆栈结构。且一般会对深度优先搜索进行深度上的限制，以免深度过深。

有界深度优先搜索算法过程：

1. 把起始节点Ｓ放到OPEN表中。如果此节点为一目标节点，则得到一个解。
2. 如果OPEN为一空表，则失败退出。
3. 把第一个节点（节点n）从OPEN表移到CLOSED表。
4. 如果节点n的深度等于最大深度dm，则转向 2 。
5. 扩展节点n ，产生其全部后裔，并把它们放入OPEN表的首部。如果没有后裔，则转向 2 。
6. 如果后继节点中有任一个为目标节点，则求得一个解， 成功退出；否则，转向 2 。

有界深度优先搜索算法的改进：

dm的值很难给出，不能保证找到最优解。可以使用可变的dm。当达了指定的dm仍未发现目标节点，且CLOSED表中仍有待扩展节点时，就将这些节点送回OPEN表，同时增大深度界限dm继续向下搜索。如此不断地增大dm，只要问题有解，就一定可以找到它。

启发式图搜索策略

启发式策略

启发式策略就是利用与问题有关的启发信息进行搜索。在状态空间搜索中，启发式被定义成一系列操作算子，并能从状态空间中选择最有希望到达问题解的 路径。

运用启发式策略的两种基本情况：

• 一个问题由于在问题陈述和数据获取方面固有的模糊性，可能会使它没有一个确定的解。
• 虽然一个问题可能有确定解，但是其状态空间特别大，搜索中生成扩展的状态数会随着搜索 的深度呈指数级增长。

启发信息和估价函数

在具体求解中，启发式搜索能够利用与该问题有关的信息来简化搜索过程，称此类信息为启发信息。启发信息按运用的方法不同可分为三种：

• 陈述性启发信息：一般被用于更准确、更精炼地描述状态，使问题的状态空间缩小，如待求问题的特定状况等属于此类信息。
• 过程性启发信息。一般被用于构造操作算子，使操作算子少而精，如一些规律性知识等属于此类信息。
• 控制性启发信息。它是表示控制策略方面的知识，包括协调整个问题求解过程中所使用的各种处理方法、搜索策略、控制结构等有关的知识。

为提高搜索效率就需要利用上述三种启发信息作为搜索的辅助性策略。这里主要介绍控制性的启发信息。利用控制性的启发信息有两种极端的情况：

• 一种是没有任何控制性知识作为搜索的依据，因而搜索的每一步完全是随意的，如随机搜索、宽度搜索、深度搜索等；
• 另一种是有充分的控制知识作为依据，因而搜索的每一步选择都是正确的，但这是不现实的。

一般情况介于二者之间。在搜索过程中需要根据这些启发信息估计各个结点的重要性。

用估价函数（Evaluation Function）估计待搜索结点的“有希望”程度，并依次给它们排定次序。一般来说，估计一个结点价值，必须综合考虑已经付出的代价和将要付出的代价两方面的因素，因此，估价函数 $f(n)$​ 定义为从初始结点经过 n 结点到达目的结的路径的最小代价估计值，其一般形式是：
$$f(n)=g(n)+h(n)$$
其中，$g(n)$ 是从初始结点到n结点的实际代价，而 $h(n)$ 是从n结点到目的结点的最佳路径的估计代价、因为实际代价$g(n)$ 可以根据已生成的搜索树实际计算出来，而估计代价 $h(n)$ 是对未生成的搜索路径的作某种经验性的估计。这种估计来源于对问题解的某些特性的认识，希望依靠这些特性来快速找到问题的解，因此主要是 $h(n)$ 体现了搜索的启发性。

A搜索算法

与宽度优先和深度优先搜索算法一样，启发式图搜索法算法也使用OPEN表和CLOSED表记录状态信息，不同的是，它既不同于宽度优先所使用的队列（先进先出），也不同于深度优先所使用的堆栈（先进后出），而是一个按状态的启发估价函数值的大小排列的一个表。进入open表的状态不是简单地排在队尾（或队首），而是根据其估值的大小插入到表中合适的位置，每次从表中优先取出启发估价函数值最小的状态加以扩展。

A算法是基于估价函数的一种加权启发式图搜索算法，具体步骤如下：

1. 把附有$f(S_0)$的初始结点$S_0$。放入OPEN表；
2. 若OPEN表为空，则搜索失败，退出；
3. 移出OPEN表中第一个结点N放入CLOSED表中，并顺序编号 n；
4. 若目标结点把附有$f(S_0)$的初始$S_g=N$，则搜索成功，结束；
5. 若$N$不可扩展，则转步骤2；
6. 扩展$N$，生成一组附有$f(x)$的子结点，对这组子结点作如下处理。
   1. 考察是否有已在OPEN表或CLOSED表中存在的结点。若有则再考察其中有无$N$的先辈结点，若有则删除之，对于其余结点也删除之，但由于它们又被第二次生成，因此需要考虑是否修改已经存在于OPEN表或CLOSED表中的这些结点及其后裔的返回指针和$f(x)$的值。修改原则是：选$f(x)$值小的路径走。
   2. 为其余子结点配上指向$N$的返回指针后放入OPEN表中，并对OPEN表按$f(x)$值以升序排序，转步骤2。

A*搜索算法

A* 搜索算法又称为最佳图搜索算法，定义$h^{\ast }(n)$为状态 n 到目的状态的最优路径的代价，则当A搜索算法的启发函数小于等于$h^{\ast }(n)$时被称为 A* 算法。

如果某一问题有解，那么利用 A* 搜索算法对该问题进行搜索则一定能搜索到解，并且一定能搜索到最优的解而结束。 A* 搜索算法有以下几个特征：

• 可采纳性：对于可解状态空间图，如果一个搜索算法在优先步内终止，并能得到最优解，就称该搜索算法是可采纳的。可证明所有 A* 搜索算法都是可采纳的，宽度优先搜索是 A* 搜索算法的一个特例，相当于 A* 搜索算法中$h(n)=0$和$f(n)=g(n)+0$，它也是可接纳的，只是效率太低。
• 单调性：对所有状态$n_i$和$n_j$，其中$n_j$是$n_i$的后裔，满足$h(n_i)-h(n_j)\le cost(n_i,n_j)$，其中$cost(n_i,n_j)$是二者之间的实际代价，且目的状态的启发函数值为0或$h(Goal)=0$，则称该启发函数是单调的。通俗的说就是在整个搜索空间都是局部可采纳的。 一个状态和任一个子状态之间的差由该状态与其子状态之间的实际代价所限定。
• 信息性：在两个 A* 启发策略的$h_1$和$h_2$中，如果对搜索空间中的任一状态 n 都有$h_1(n)\le h_2(n)$，就称策略 $h_2$ 比 $h_1$ 具有更多的信息性。