顶点从观察空间变换到裁剪空间

顶点从观察空间变换到裁剪空间

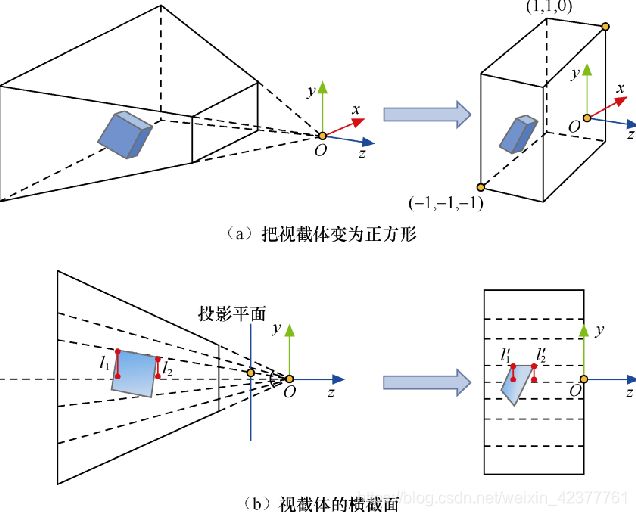
1.视截体

视截体简单的说就是摄像机的可视区域。
一个正交视图的摄像机，他的视截体是一个长方体。而一个使用了透视视图的摄像机，它的视截体则是一个正棱台。

视截体由多个因素决定。
1.field of view：视野区域角度，一般是只要知道竖直方向的角度。因为水平方向的视野可以通过aspect参数推出。如上图的∠UOD.
2.aspect：正棱台的宽高比。W / H。
3.far：视截体的远截面距离摄像机的距离。
4.near：视截体的近截面距离摄像机的距离。

2.投影矩阵

通过投影矩阵，可以把观察空间里的正棱台视截体形变拉伸为一个长方体的裁剪空间。

裁剪空间在经由透视除法之后，才会转化到宽高取值范围为[-1,1]，深度取值为[-1,0]的长方体方体（Direct3D平台）。这种投影变换称为透视投影。转化后的空间叫标准化设备坐标（NDC）。
下面尝试推导下投影矩阵。
假设视截体里的一个点P（x,y,z）,经过透视投影后转变为NDC坐标的P1(x1, y1, z1)。

因为NDC空间的高度正是2，并且在NDC空间中，PP1//AA1。那么上图的OP与蓝色投影线相交的P1点的高度值y1，就是转化到NDC空间后的P1点的y1值。
现在我们知道摄像机的参数有 纵角度FoY，远近截面f，n，宽高比aspect。
$$\angle UO{A}_1=FoY$$
$$\left|U{A}_1\right|=1$$
$$z_1=-\left|A_{1}O\right|=-ctan(\frac{\angle UO{A}_1}{2})=-ctan(\frac{FoY}{2})$$
因为△OPA和△OP1A1相似。有
$$\frac{y_1}{z_1}=\frac{y}{z}$$
可以先求得投影后的y1值为
$$y_1=\frac{y}{z}.z_1=-\frac{y}{z}.ctan(\frac{FoY}{2})..........①$$
同理，我们可以把符号y更换为符号x，符号FoY更换为FoX，就可以求得x1的等式。
$$x_1=\frac{x}{z}.z_1=-\frac{x}{z}.ctan(\frac{FoX}{2})..........②$$

因为FoX参数未知，我们可以通过已知的aspect和FoY参数，替换掉它。如下图

$$aspect=\frac{W}{H}=\frac{ctan(\frac{FoY}{2}).z_1}{ctan(\frac{FoX}{2}).z_1}$$
$$ctan(\frac{FoX}{2})=\frac{ctan(\frac{FoY}{2})}{aspect}..........③$$
③式代入②式后
$$x_1=\frac{x}{z}.z_1=-\frac{x}{z}.\frac{ctan(\frac{FoY}{2})}{aspect}$$
P1的x1，y1的表达式已经有了，P1新的坐标表示为
$$P_1=[-\frac{x}{z}.\frac{ctan(\frac{FoY}{2})}{aspect},-\frac{y}{z}.ctan(\frac{FoY}{2}),z_1]$$
齐次化的P1的坐标
$$P_1=[-\frac{x}{z}.\frac{ctan(\frac{FoY}{2})}{aspect},-\frac{y}{z}.ctan(\frac{FoY}{2}),z_1,1]$$
根据齐次坐标的性质，如果第四维w≠0，则（x，y，z，1）等价于（wx，wy，wz，w）。现在把P1 的坐标值乘以−z后
$$P_1=[x.\frac{ctan(\frac{FoY}{2})}{aspect},y.ctan(\frac{FoY}{2}),-z.z_1,-z]..........④$$
通过观察P1表达式的特点，P1可以拆分为点（x,y,z,1）右乘一个矩阵Mp
$$P_1=\left[\begin{array}{cccc}\frac{ctan(\frac{FoY}{2})}{aspect}& 1& 1& 1\\ 1& ctan(\frac{FoY}{2})& 1& 1\\ m1& m2& m3& m4\\ 0& 0& -1& 0\end{array}\right].\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$$
$$M_p=\left[\begin{array}{cccc}\frac{ctan(\frac{FoY}{2})}{aspect}& 1& 1& 1\\ 1& ctan(\frac{FoY}{2})& 1& 1\\ m1& m2& m3& m4\\ 0& 0& -1& 0\end{array}\right]$$
矩阵Mp中的m1 m2 m3 m4是未知的，且有一下表达式成立
$$-z.z_1=m1.x+m2.y+m3.z+m4$$
通过观察式子，可以猜想m1 = 0， m2 = 0（因为式子的左边不存在x和y）。这个也是必然的。因为对于P点，投影到投影面后，z1值都必定一致且和xy的取值无关。

所以上式进一步简化
$$-z.z_1=m3.z+m4$$
投影后z1的取值范围是[−1，0]，显然远截面的z（即−f）投影后的z1 为−1，近截面的z（即−n）投影后z1 为0。把值代入上式解二元一次方程
$$\begin{array}{r}\{\begin{array}{l}-f\cdot m_3+m_4=f\left(-1\right)\\ m_3\left(-n\right)+m_4=n\left(0\right)\end{array}\\ .\end{array}$$
求得m3 m4的表达式
$$m_3=\frac{f}{f-n}$$
$$m_4=\frac{nf}{f-n}$$

最后求得Mp的表达式为
$$M_p=\left[\begin{array}{cccc}\frac{ctan(\frac{FoY}{2})}{aspect}& 1& 1& 1\\ 1& ctan(\frac{FoY}{2})& 1& 1\\ 0& 0& \frac{f}{f-n}& \frac{nf}{f-n}\\ 0& 0& -1& 0\end{array}\right]$$
Mp就是我们的投影矩阵。
最后有一个需要注意的，我们的观察空间使用的是右手坐标系，而裁剪空间采用左手坐标系，要把Mp右乘一个倒转z轴的矩阵才能得到最终的投影矩阵Mp。
$$M_p=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& -1& 0\\ 0& 0& 0& 1\end{array}\right].\left[\begin{array}{cccc}\frac{ctan(\frac{FoY}{2})}{aspect}& 1& 1& 1\\ 1& ctan(\frac{FoY}{2})& 1& 1\\ 0& 0& \frac{f}{f-n}& \frac{nf}{f-n}\\ 0& 0& -1& 0\end{array}\right]$$
$$M_p=\left[\begin{array}{cccc}\frac{ctan(\frac{FoY}{2})}{aspect}& 1& 1& 1\\ 1& ctan(\frac{FoY}{2})& 1& 1\\ 0& 0& \frac{f}{n-f}& \frac{nf}{n-f}\\ 0& 0& -1& 0\end{array}\right]$$
因为在④的时候为了转化齐次坐标，乘了-z值。所以投影矩阵Mp乘以P点得到到的裁剪空间的P1坐标的w值并非为1，也即使说，P1点没有做透视除法。最后要把的到的P1点的所有坐标值除以它的w值（也是P点的z值），后才是NDC中的坐标值。
$$P_{NDC}=\frac{M_p.P}{w}$$

推导完结了。

3.举个栗子

现在有一个物体Cube，它呆在一个使用透视的摄像机前。我们可以在Unity通过坐标转化的方式，模拟它投影到屏幕前的样子。

所用到的场景中的物体有
一个透视投影的摄像机 MainCamera
一个任你摆布的模型cube Cube
一个表示NDC空间原点的空物体 ndcspace，这个空物体摆在世界坐标的原点。

步骤：
1.取得模型上的所有顶点
2.顶点坐标需要转化->世界坐标->观察空间坐标P。
3.P点右乘Mp投影矩阵，就可以的得到一个裁剪空间上的坐标P1。
3.P1还需要做透视除法处理：除以P1的w分量。
4.把所有的生成的P1点通过mesh连接起来，生成一个新的cube，放置在ndcspace节点的位置。
5.把Game视图的窗口设置为1：1，因为要和我们生成的NDC空间大小要一致，方便查看效果。
6.在scene视图，选择正交模式，沿着z轴的正方向观察ndcspace节点。

移动cube，观察生成的mesh和屏幕上的cube的投影。

在scene视图正交模式观察的mesh的表现，和投影在屏幕的cube的表现完全一致。

把cube拖到右上角，和屏幕的右上对其，mesh也和NDC的边缘对齐。

工程地址

矩阵的推导部分思路来自 《unity3d内建着色器源码剖析》一书，有解读的不对的地方望大佬们指出。