2.14---python z3库---IDA远程调试Linux程序
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档
文章目录
- 一. z3线性约束求解学习
-
- 1.解不等式
- 2.简化器
- 3.
- 4.表达式分析
- 5.数学运算
- 6.精度设置
- 7.创建有理数，实数
- 8. 不可满足/无解
- 9.布尔逻辑
- 10.布尔常量 True 和 False 可用于构建 Z3 布尔表达式
- 11.多项式和布尔约束的组合
- 12. SOLVERS 求解器
-
- 12.1 pop / push 断言堆栈
- 12.2 unknown
-
- 12.3 遍历约束及检查方法
- 13. 算术
- 14. 函数
- 二. IDA远程调试Linux程序
-
- 1. IDA调试器
-
- 1.1 加载目标文件
- 1.2 调试器界面
- 1.3 调试跟踪
- 1.4 断点
- 1.5 跟踪
- 2.远程调试(Linux)
- 三. 练习题
一. z3线性约束求解学习
注：print () python3要加括号，python2不加
1.解不等式
from z3 import *
x= Int('x')
y= Int('y')
solve(x>2,y<10,x+2*y==7)
# 输出[y = 0, x = 7]
- 函数 Int（‘x’） 在 Z3 中创建一个名为 x 的整数变量
- 像Python一样的Z3Py使用=进行赋值。运算符<、<=、>、>=、== 和 ！= 进行比较
2.简化器
from z3 import *
x = Int('x')
y = Int('y')
print (simplify(x + y + 2*x + 3))
# 输出3 + 3*x + y
- 这是Z3 公式/表达式简化器。
3.
from z3 import *
x = Int('x')
y = Int('y')
print x**2 + y**2 >= 1
set_option(html_mode=False)
print x**2 + y**2 >= 1
set_option(html_mode=True)
print x**2 + y**2 >= 1
输出：
x**2 + y**2 >= 1
x**2 + y**2 >= 1
x<sup>2</sup> + y<sup>2</sup> ≥ 1
- x2 就表示x的平方
- 命令set_option(html_mode = False)使得所有公式和表达式以Z3Py表示法显示。
- Z3使用数学符号显示公式和表达式。∧是逻辑和，∨是逻辑或
4.表达式分析
from z3 import *
x = Int('x')
y = Int('y')
n = x + y >= 3
print "num args: ", n.num_args()
print "children: ", n.children()
print "1st child:", n.arg(0)
print "2nd child:", n.arg(1)
print "operator: ", n.decl()
print "op name: ", n.decl().name()
num args: 2
children: [x + y, 3]
1st child: x + y
2nd child: 3
operator: >=
op name: >=
5.数学运算
from z3 import *
x = Real('x')
y = Real('y')
solve(x**2 + y**2 > 3, x**3 + y < 5)
[y = 2, x = 1/8]
- Real(‘x’)创建实际变量x。 Z3可以表示任意大的整数，有理数和无理数。 一个无理数是具有整数系数的多项式的根。 在内部，Z3精确地代表了所有这些数字。 无理数以十进制表示形式显示，以便读取结果。
- Z3 提供所有基本的数学运算。Z3Py使用与Python语言相同的运算符优先级。 像Python一样，**是幂运算符。Z3可以求解非线性多项式约束。
6.精度设置
x = Real('x')
y = Real('y')
solve(x**2 + y**2 == 3, x**3 == 2)
set_option(precision=30)
print "Solving, and displaying result with 30 decimal places"
solve(x**2 + y**2 == 3, x**3 == 2)
[x = 1.2599210498?, y = -1.1885280594?]
Solving, and displaying result with 30 decimal places
[x = 1.259921049894873164767210607278?,
y = -1.188528059421316533710369365015?]
- 选项set_option(precision = 30)设置显示结果时使用的小数位数。 这个？ 标记在1.2599210498？ 中表示输出被截断。
7.创建有理数，实数
- 过程 Q（num， den） 创建一个 Z3 有理数，其中 num 是分子，den 是分母。
- RealVal（1） 创建一个 Z3 实数 代表数字 1。
print RealVal(1)/3
print Q(1,3)
x = Real('x')
print x + Q(1,3)
print x + "1/3"
print x + 0.25
输出：1/3 1/3
- 这是第一行第二行的输出结果，当然也可以用十进制表示
x = Real('x')
solve(3*x == 1)
set_option(rational_to_decimal=True)
solve(3*x == 1)
set_option(precision=30)
solve(3*x == 1)
[x = 1/3]
[x = 0.3333333333?]
[x = 0.333333333333333333333333333333?]
8. 不可满足/无解
- 约束系统也可能没有解决方案。 在这种情况下，我们说这个系统是不可满足的。
x = Real('x')
solve(x > 4, x < 0)
no solution
9.布尔逻辑
- Z3支持布尔运算符：And, Or, Not, Implies (implication), If (if-then-else)。双含义符号用==表示。 以下示例显示如何解决一组简单的布尔约束。
p = Bool('p')
q = Bool('q')
r = Bool('r')
solve(Implies(p, q), r == Not(q), Or(Not(p), r))
[q = False, p = False, r = True]
- P / Q
F = Or(P, Q) - solve()函数来检查可满足性，这个solve()函数将创建一个solver实例来检验命题的可满足性，并且如果命题可满足的话输出一个模型
- Z3支持连接词：/(And), /(Or), ~(Not), ->(Implies)
- implies：设p、q为两个命题。复合命题"如果p，则q"称为p与q的蕴含式，记作p→q。并称p为蕴含式的前件，q为后件。并规定p→q为假当且仅当p为真q为假。
10.布尔常量 True 和 False 可用于构建 Z3 布尔表达式
p = Bool('p')
q = Bool('q')
print And(p, q, True)
print simplify(And(p, q, True))
print simplify(And(p, False))
And(p, q, True)
And(p, q)
False
11.多项式和布尔约束的组合
p = Bool('p')
x = Real('x')
solve(Or(x < 5, x > 10), Or(p, x**2 == 2), Not(p))
[x = -1.4142135623?, p = False]
12. SOLVERS 求解器
12.1 pop / push 断言堆栈
x = Int('x')
y = Int('y')
s = Solver()
print s
s.add(x > 10, y == x + 2)
print s
print "Solving constraints in the solver s ..."
print s.check()
print "Create a new scope..."
s.push()
s.add(y < 11)
print s
print "Solving updated set of constraints..."
print s.check()
print "Restoring state..."
s.pop()
print s
print "Solving restored set of constraints..."
print s.check()
[]
[x > 10, y == x + 2]
Solving constraints in the solver s ...
sat
Create a new scope...
[x > 10, y == x + 2, y < 11]
Solving updated set of constraints...
unsat
Restoring state...
[x > 10, y == x + 2]
Solving restored set of constraints...
sat
- 一开始求解器为空，后来加上两个断言之后，求解器有了那两个断言。check求解器得到结果。sat 意味着满足（satisfied）。接下来创建了一个新的范围，可以看到新增了一个断言，这时候check的结果就是unsat，意味着不可满足（unsatisfied）. 再把新增的assert 弹出（pop）之后，可以看到又sat了。
- Solver()命令创建一个通用求解器。
- 约束可以使用方法add添加。
- 方法check()解决了断言的约束。
- 如果找到解决方案，结果是sat（满足）。如果不存在解决方案，结果unsat（不可满足）。
- 命令push通过保存当前堆栈大小来创建一个新的作用域。命令pop删除它与匹配推送之间执行的任何断言。检查方法始终对求解器断言堆栈的内容进行操作。
12.2 unknown
x = Real('x')
s = Solver()
s.add(2**x == 3)
print s.check()
unknown
- Z3可以求解非线性多项式约束，但2 ** x不是一个多项式。
12.3 遍历约束及检查方法
- 当 Z3 找到断言约束集的解决方案时，命令检查将返回 sat。 我们说 Z3 满足了一组约束。我们说解决方案是断言集合的模型 约束。模型是一种解释，它使每个断言约束都为真。 以下示例显示了检查模型的基本方法。
x, y, z = Reals('x y z')
s = Solver()
s.add(x > 1, y > 1, x + y > 3, z - x < 10)
print s.check()
m = s.model()
print "x = %s" % m[x]
print "traversing model..."
for d in m.decls():
print "%s = %s" % (d.name(), m[d])
- 表达式 m[x] 返回模型中 x 的解释。 表达式 “%s = %s” % （d.name（）， m[d]） 返回一个字符串，其中第一个 %s 替换为 d 的名称（即 d.name（）），第二个 %s 具有 D的解释（即m[d]）。
13. 算术
x = Real('x')
y = Int('y')
a, b, c = Reals('a b c')
s, r = Ints('s r')
print x + y + 1 + (a + s)
print ToReal(y) + c
- 函数 ToReal 将整数表达式强制转换为实数表达式。
- 支持所有基本的算术运算
14. 函数
- 设不解释的整数常量（又名变量）x，y；设f是一个不解释函数，它接受一个类型（又名 sort）整数的参数并生成一个整数值。
x = Int('x')
y = Int('y')
f = Function('f', IntSort(), IntSort())
solve(f(f(x)) == x, f(x) == y, x != y)
输出：
[x = 0, y = 1, f = [0 -> 1, 1 -> 0, else -> 1]]
- f（0）= 1，f（1）= 0，并且对于全部不同于0和1的a， f（a）=1。
二. IDA远程调试Linux程序
1. IDA调试器
1.1 加载目标文件
1.2 调试器界面
1.3 调试跟踪
- F7，单步步进，遇到call指令跟进
- F8，单步步过，不跟进call指令
- F4，运行到光标所在行
- F9，运行程序
- F2，设置断点
1.4 断点
- 可以为断点在condition中设置条件断点
1.5 跟踪
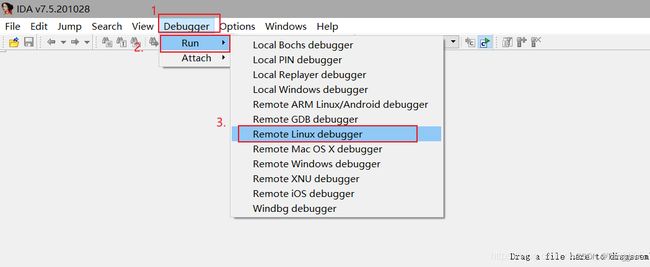
2.远程调试(Linux)
-
物理机作为调试器客户端，在其上运行的虚拟机作为目标文件的运行环境。
-
我们还需要在虚拟机里面运行相应的调试服务器组件（处理所有底层执行和调试操作），调试服务器组件可以在ida安装目录下的dbgsrv文件中找到，不同系统需要选择不同的组件传到虚拟机中。
-
将linux_server64（如果是虚拟机是32位系统就用inux_server）和待调试的文件(main)传到linux虚拟机中，放在/home目录下。
-
先在当前目录下进入terminal命令行输入如下指令赋予两个文件权限，
-
chmod +x linux_server64 chmod +x 你的待调试文件名 详细Linux命令看菜鸟教程Linux chmod命令 记得空格隔开 -
接下来输入如下指令运行调试服务器组件，设置连接密码
-
./linux_server64 -P123456 注意前面./后没空格 -
根据你待调试的目标文件字长选择相应的ida
-
设置好后就可以远程调试了
-
以上参考文章 http://t.csdn.cn/I8tvM
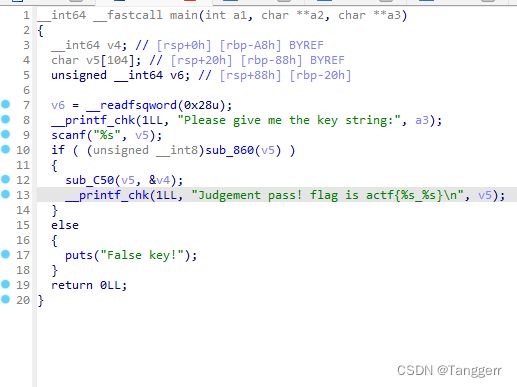
三. 练习题
- 拖进DIE中，看看
- 发现是无壳的64位ELF文件，再直接搞进IDA中
- 找到字符串，再找到主函数
- 找到关键函数，sub_860
bool __fastcall sub_860(char *a1)
{
int v1; // ecx
int v2; // esi
int v3; // edx
int v4; // r9d
int v5; // r11d
int v6; // ebp
int v7; // ebx
int v8; // r8d
int v9; // r10d
bool result; // al
int v11; // [rsp+0h] [rbp-38h]
v1 = a1[1];
v2 = *a1;
v3 = a1[2];
v4 = a1[3];
v5 = a1[4];
v6 = a1[6];
v7 = a1[5];
v8 = a1[7];
v9 = a1[8];
result = 0;
if ( -85 * v9 + 58 * v8 + 97 * v6 + v7 + -45 * v5 + 84 * v4 + 95 * v2 - 20 * v1 + 12 * v3 == 12613 )
{
v11 = a1[9];
if ( 30 * v11 + -70 * v9 + -122 * v6 + -81 * v7 + -66 * v5 + -115 * v4 + -41 * v3 + -86 * v1 - 15 * v2 - 30 * v8 == -54400
&& -103 * v11 + 120 * v8 + 108 * v7 + 48 * v4 + -89 * v3 + 78 * v1 - 41 * v2 + 31 * v5 - (v6 << 6) - 120 * v9 == -10283
&& 71 * v6 + (v7 << 7) + 99 * v5 + -111 * v3 + 85 * v1 + 79 * v2 - 30 * v4 - 119 * v8 + 48 * v9 - 16 * v11 == 22855
&& 5 * v11 + 23 * v9 + 122 * v8 + -19 * v6 + 99 * v7 + -117 * v5 + -69 * v3 + 22 * v1 - 98 * v2 + 10 * v4 == -2944
&& -54 * v11 + -23 * v8 + -82 * v3 + -85 * v2 + 124 * v1 - 11 * v4 - 8 * v5 - 60 * v7 + 95 * v6 + 100 * v9 == -2222
&& -83 * v11 + -111 * v7 + -57 * v2 + 41 * v1 + 73 * v3 - 18 * v4 + 26 * v5 + 16 * v6 + 77 * v8 - 63 * v9 == -13258
&& 81 * v11 + -48 * v9 + 66 * v8 + -104 * v6 + -121 * v7 + 95 * v5 + 85 * v4 + 60 * v3 + -85 * v2 + 80 * v1 == -1559
&& 101 * v11 + -85 * v9 + 7 * v6 + 117 * v7 + -83 * v5 + -101 * v4 + 90 * v3 + -28 * v1 + 18 * v2 - v8 == 6308 )
{
return 99 * v11 + -28 * v9 + 5 * v8 + 93 * v6 + -18 * v7 + -127 * v5 + 6 * v4 + -9 * v3 + -93 * v1 + 58 * v2 == -1697;
}
}
return result;
}
- 看到这一大堆数，很自然的想到z3库
- 逻辑简单，就是if语句，且我们若想得到flag，result不能作为返回值，而直接返回那一串式子，且算式必须为真
- 先写个脚本解出result
from z3 import *
s = Solver()
v1 = Int('v1')
v2 = Int('v2')
v3 = Int('v3')
v4 = Int('v4')
v5 = Int('v5')
v6 = Int('v6')
v7 = Int('v7')
v8 = Int('v8')
v9 = Int('v9')
v11 = Int('v11')
s.add(-85 * v9 + 58 * v8 + 97 * v6 + v7 + -45 * v5 + 84 * v4 + 95 * v2 - 20 * v1 + 12 * v3 == 12613)
s.add(30 * v11 + -70 * v9 + -122 * v6 + -81 * v7 + -66 * v5 + -115 * v4 + -41 * v3 + -86 * v1 - 15 * v2 - 30 * v8 == -54400)
s.add(-103 * v11 + 120 * v8 + 108 * v7 + 48 * v4 + -89 * v3 + 78 * v1 - 41 * v2 + 31 * v5 - (v6 *64) - 120 * v9 == -10283)
s.add(71 * v6 + (v7 *128) + 99 * v5 + -111 * v3 + 85 * v1 + 79 * v2 - 30 * v4 - 119 * v8 + 48 * v9 - 16 * v11 == 22855)
s.add(5 * v11 + 23 * v9 + 122 * v8 + -19 * v6 + 99 * v7 + -117 * v5 + -69 * v3 + 22 * v1 - 98 * v2 + 10 * v4 == -2944)
s.add(-54 * v11 + -23 * v8 + -82 * v3 + -85 * v2 + 124 * v1 - 11 * v4 - 8 * v5 - 60 * v7 + 95 * v6 + 100 * v9 == -2222)
s.add(-83 * v11 + -111 * v7 + -57 * v2 + 41 * v1 + 73 * v3 - 18 * v4 + 26 * v5 + 16 * v6 + 77 * v8 - 63 * v9 == -13258)
s.add(81 * v11 + -48 * v9 + 66 * v8 + -104 * v6 + -121 * v7 + 95 * v5 + 85 * v4 + 60 * v3 + -85 * v2 + 80 * v1 == -1559)
s.add(101 * v11 + -85 * v9 + 7 * v6 + 117 * v7 + -83 * v5 + -101 * v4 + 90 * v3 + -28 * v1 + 18 * v2 - v8 == 6308)
s.add(99 * v11 + -28 * v9 + 5 * v8 + 93 * v6 + -18 * v7 + -127 * v5 + 6 * v4 + -9 * v3 + -93 * v1 + 58 * v2 == -1697)
if s.check() == sat:
result = s.model()
print result
[v1 = 48,
v6 = 95,
v2 = 70,
v4 = 82,
v11 = 64,
v3 = 117,
v5 = 84,
v9 = 119,
v8 = 55,
v7 = 121]
- 这就是结果，然后看主函数中的if
- 找到关键函数，sub_C50
unsigned __int64 __fastcall sub_C50(const char *a1, _BYTE *a2)
{
size_t v4; // rax
unsigned int v5; // edx
int v6; // edi
int v7; // ecx
__int64 v8; // r8
__int128 *v9; // rsi
unsigned int v10; // ecx
int v11; // eax
int v12; // edi
int v13; // edx
int v14; // eax
_BYTE *v15; // rsi
_BYTE *v16; // rcx
_BYTE *v17; // r8
int *i; // rax
unsigned __int64 result; // rax
__int128 v20[2]; // [rsp+0h] [rbp-48h] BYREF
__int64 v21; // [rsp+20h] [rbp-28h]
unsigned __int64 v22; // [rsp+28h] [rbp-20h]
v22 = __readfsqword(0x28u);
memset(v20, 0, sizeof(v20));
v21 = 0LL;
v4 = strlen(a1);
v5 = 0;
v6 = 9;
while ( v5 < v4 )
{
v7 = a1[v5++];
v6 ^= v7;
}
if ( v6 )
{
v8 = 0LL;
v9 = v20;
while ( 1 )
{
v9 = (__int128 *)((char *)v9 + 4);
v10 = v8 + 1;
v11 = v6 / 10;
v12 = v6 % 10;
*((_DWORD *)v9 - 1) = v12;
LOBYTE(v13) = v12;
v6 = v11;
if ( !v11 )
break;
v8 = v10;
}
v14 = v8 - 1;
v15 = a2;
v16 = &a2[v10];
v17 = &a2[v8];
for ( i = (int *)v20 + v14; ; --i )
{
*v15 = v13 + 48;
if ( v17 == v15 )
break;
v13 = *i;
++v15;
}
}
else
{
v16 = a2;
}
result = __readfsqword(0x28u) ^ v22;
*v16 = 0;
return result;
}
- 将我们得到的v5 F0uRTy_7w@输入至程序中，运行即得flag
- 我们此时需要用linux系统下的虚拟机进行运行
- 上图是动态调试，这题用不着
- 终于，我们成功的发现了flag{F0uRTy_7w@_42}