Zama TFHE-rs白皮书(2)
前序博客有:
- 基于[Discretized] Torus的全同态加密指引(1)
- 基于[Discretized] Torus的全同态加密指引(2)
- TFHE——基于[Discretized] Torus的全同态加密 代码解析
- Zama TFHE-rs
- Zama TFHE-rs白皮书(1)
Zama TFHE-rs白皮书,见:
- Zama团队Ilaria Chillotti、Marc Joye、Pascal Paillier论文《Programmable Bootstrapping Enables Efficient Homomorphic Inference of Deep Neural Networks∗》。
4. Programmable Bootstrapping可编程自举
Programmable Bootstrapping可编程自举为bootstrapping技术的扩展,支持重置噪声到某固定级别,与此同时,对输入密文做某函数evaluate。
本节将详细介绍如何做常规bootstrapping,然后继续到可编程自举,同时展示如何将任意函数表示为look-up table来做evaluate。当可编程自举中的 f f f为identity函数时,其就是常规自举。
4.1 blind rotation
Gentry的bootstrapping为:
- 对某密文自身的解密密钥加密,使用该加密后的解密密钥,来对该密文进行同态解密,与此同时降低该密文中的噪声。
4.1.1 Intuition
Intuition:
对于 L W E ‾ \overline{LWE} LWE密文 c ˉ ← L W E ‾ s ( μ ˉ ) = ( a ˉ 1 , ⋯ , a ˉ n , b ˉ ) ∈ ( Z / q Z ) n + 1 \bar{c}\leftarrow\overline{LWE}_{\mathbf{s}}(\bar{\mu})=(\bar{a}_1,\cdots,\bar{a}_n,\bar{b})\in(\mathbb{Z}/q\mathbb{Z})^{n+1} cˉ←LWEs(μˉ)=(aˉ1,⋯,aˉn,bˉ)∈(Z/qZ)n+1,其中:
- a ˉ j ← § Z / q Z \bar{a}_j\xleftarrow{\S} \mathbb{Z}/q\mathbb{Z} aˉj§Z/qZ
- b ˉ = ∑ j = 1 n s j a ˉ j + μ ˉ ∗ \bar{b}=\sum_{j=1}^{n}s_j\bar{a}_j+\bar{\mu}^* bˉ=∑j=1nsjaˉj+μˉ∗,其中 μ ˉ ∗ = μ ˉ + e ˉ \bar{\mu}^*=\bar{\mu}+\bar{e} μˉ∗=μˉ+eˉ,离散噪声 e ˉ = ⌈ e q ⌋ ( m o d q ) \bar{e}=\lceil eq\rfloor(\mod q) eˉ=⌈eq⌋(modq), e ← N ( 0 , σ 2 ) e\leftarrow \mathcal{N}(0,\sigma^2) e←N(0,σ2)。
- 密文 c ˉ \bar{c} cˉ,为基于私钥 s = ( s 1 , ⋯ , s n ) ∈ B n \mathbf{s}=(s_1,\cdots,s_n)\in\mathbb{B}^n s=(s1,⋯,sn)∈Bn,对明文 μ ˉ ∈ Z / q Z \bar{\mu}\in \mathbb{Z}/q\mathbb{Z} μˉ∈Z/qZ的加密。
- 使用私钥 s \mathbf{s} s,对密文 c ˉ \bar{c} cˉ解密分为2步:
- μ ˉ ∗ ← b ˉ − ∑ j = 1 n s j a ˉ j \bar{\mu}^*\leftarrow \bar{b}-\sum_{j=1}^{n}s_j\bar{a}_j μˉ∗←bˉ−∑j=1nsjaˉj
- μ ˉ ← U p p e r q , p ( μ ˉ ∗ ) \bar{\mu}\leftarrow Upper_{q,p}(\bar{\mu}^*) μˉ←Upperq,p(μˉ∗)
为bootstrap,可将(无rounding)的解密看成是:
− μ ˉ ∗ = − b ˉ + ∑ j = 1 n s j a ˉ j ( m o d q ) -\bar{\mu}^*= -\bar{b}+\sum_{j=1}^{n}s_j\bar{a}_j(\mod q) −μˉ∗=−bˉ+∑j=1nsjaˉj(modq)
将该值作为 X X X的指数,获得单项式 X − μ ˉ ∗ X^{-\bar{\mu}^*} X−μˉ∗。注意, μ ˉ ∗ \bar{\mu}^* μˉ∗有 q q q个可能的取值。粗略的思想为,对于所有可能的 μ ˉ ∗ \bar{\mu}^* μˉ∗值,构建多项式——test polynomial,使得其每个系数都编码了对应 μ ˉ ∗ \bar{\mu}^* μˉ∗的无噪声值,即 μ ˉ = U p p e r q , p ( μ ˉ ∗ ) \bar{\mu}= Upper_{q,p}(\bar{\mu}^*) μˉ=Upperq,p(μˉ∗)。
特别地,假设该test polynomial为degree- q q q多项式 v ˉ = v ˉ 0 + v ˉ 1 X + ⋯ + v ˉ q − 1 X q − 1 \bar{v}=\bar{v}_0+\bar{v}_1X+\cdots+\bar{v}_{q-1}X^{q-1} vˉ=vˉ0+vˉ1X+⋯+vˉq−1Xq−1,则其第 i i i个系数设置为 v ˉ i = U p p e r q , p ( i m o d q ) \bar{v}_i=Upper_{q,p}(i\mod q) vˉi=Upperq,p(imodq)。
通过对该test polynomial v ˉ \bar{v} vˉ rotate μ ˉ ∗ \bar{\mu}^* μˉ∗ 个位置, μ ˉ \bar{\mu} μˉ值就移至了常量系数位置,然后剩下的就是extract该值了。如下图所示:

当然,该rotation是同态进行的,因此名为blind rotation。同时,由于 X − μ ˉ ∗ ⋅ v ˉ X^{-\bar{\mu}^*}\cdot \bar{v} X−μˉ∗⋅vˉ为多项式,这正是 G L W E ‾ \overline{GLWE} GLWE加密所要处理的。
G L W E ‾ \overline{GLWE} GLWE中的多项式都是基于模 X N + 1 X^N+1 XN+1定义的。这即意味着 X X X为 Z N [ X ] \mathbb{Z}_N[X] ZN[X]中order为 2 N 2N 2N的multiplicative元素。【 X N + i ≡ − X i ( m o d X N + 1 ) X^{N+i}\equiv -X^i(\mod X^N+1) XN+i≡−Xi(modXN+1),从而有 X N ≡ − 1 ( m o d X N + 1 ) X^{N}\equiv -1(\mod X^N+1) XN≡−1(modXN+1),以及 X 2 N ≡ 1 ( m o d X N + 1 ) X^{2N}\equiv 1(\mod X^N+1) X2N≡1(modXN+1)。】
但是在 L W E ‾ \overline{LWE} LWE加密中, μ ˉ ∗ \bar{\mu}^* μˉ∗是基于模 q q q定义的。因此,需要将其rescale为模 2 N 2N 2N。因此,不适用relation − μ ˉ ∗ = − b ˉ + ∑ j = 1 n s j a ˉ j ( m o d q ) -\bar{\mu}^*= -\bar{b}+\sum_{j=1}^{n}s_j\bar{a}_j(\mod q) −μˉ∗=−bˉ+∑j=1nsjaˉj(modq),而实际依赖于其近似值:
− μ ~ ∗ = − b ~ + ∑ j = 1 n s j a ~ j ( m o d 2 N ) -\tilde{\mu}^*= -\tilde{b}+\sum_{j=1}^{n}s_j\tilde{a}_j(\mod 2N) −μ~∗=−b~+∑j=1nsja~j(mod2N)
其中:
- b ~ = ⌈ 2 N ( b ˉ m o d q ) q ⌋ \tilde{b}=\lceil \frac{2N(\bar{b}\mod q)}{q}\rfloor b~=⌈q2N(bˉmodq)⌋
- a ~ j = ⌈ 2 N ( a ˉ j m o d q ) q ⌋ \tilde{a}_j=\lceil \frac{2N(\bar{a}_j\mod q)}{q}\rfloor a~j=⌈q2N(aˉjmodq)⌋
这种近似可能会生成一个小的额外error添加到噪声中。称该额外error为drift:
- drift 同时依赖 L W E ‾ \overline{LWE} LWE的size n n n,和, G L W E ‾ \overline{GLWE} GLWE中的ring size N N N
- 可通过小心选择参数,可处理drift对结果的影响。
同时,因为test polynomial v ˉ \bar{v} vˉ 属于 Z ^ N [ X ] \hat{\mathbb{Z}}_N[X] Z^N[X],因此其由 N N N个系数,最多可编码 N N N个 μ ~ ∗ \tilde{\mu}^* μ~∗值——对应的解决方案为,确保 μ ~ ∗ \tilde{\mu}^* μ~∗的最高有效位为 0 0 0,即要求参数 w ˉ ≥ 1 \bar{w}\geq 1 wˉ≥1。此时, μ ~ ∗ \tilde{\mu}^* μ~∗最多有 N N N个可能值,该test polynomial v ˉ = v ˉ 0 + ⋯ + v ˉ N − 1 X N − 1 \bar{v}=\bar{v}_0+\cdots+\bar{v}_{N-1}X^{N-1} vˉ=vˉ0+⋯+vˉN−1XN−1,其中:
v ˉ i = U p p e r q , p ( q 2 N i m o d q ) \bar{v}_i=Upper_{q,p}(\frac{q}{2N}i\mod q) vˉi=Upperq,p(2Nqimodq)。
4.1.2 implementation
接下来将解释在 G L W E ‾ \overline{GLWE} GLWE加密情况下,如何计算 X − μ ~ ∗ X^{-\tilde{\mu}^*} X−μ~∗与test polynomial v ˉ \bar{v} vˉ 之间的乘积——可通过一系列CMux gates来实现。
用于加密 L W E ‾ \overline{LWE} LWE密文的私钥bits s j s_j sj是不可公开的。基于某加密密钥 s ′ ∈ B N [ X ] k \mathfrak{s}'\in\mathbb{B}_N[X]^k s′∈BN[X]k,对 L W E ‾ \overline{LWE} LWE私钥逐bit做 G G S W ‾ \overline{GGSW} GGSW加密,可获得bootstrapping keys——对于所有的 j = 1 , ⋯ , n j=1,\cdots,n j=1,⋯,n,有:
b s k [ j ] ← G G S W ‾ s ′ ( s j ) bsk[j]\leftarrow \overline{GGSW}_{\mathfrak{s}'}(s_j) bsk[j]←GGSWs′(sj)。
对应的blind rotation算法见Algorithm 1:

Blind rotation算法中,循环结束时, A C C ACC ACC包含了,基于key s ′ \mathfrak{s}' s′ 对 X − μ ~ ∗ ⋅ v ˉ X^{-\tilde{\mu}^*}\cdot \bar{v} X−μ~∗⋅vˉ 做 G L W E ‾ \overline{GLWE} GLWE 加密的密文。
以 c ˉ j ′ \bar{\mathfrak{c}}_j' cˉj′来表示Algorithm 1中 i = j i=j i=j时 accumulator A C C ACC ACC 的值。则有:
c ˉ j ′ ← G L W E ‾ s ′ ( X − b ~ + ∑ i = 1 j s i a ~ i ⋅ v ˉ ) \bar{\mathfrak{c}}_j'\leftarrow \overline{GLWE}_{\mathfrak{s}'}(X^{-\tilde{b}+\sum_{i=1}^{j}s_i\tilde{a}_i}\cdot \bar{v}) cˉj′←GLWEs′(X−b~+∑i=1jsia~i⋅vˉ)。
令 c ˉ ′ = c ˉ n \bar{\mathfrak{c}}'=\bar{\mathfrak{c}}_n cˉ′=cˉn,则有:
c ˉ ′ ← G L W E ‾ s ′ ( X − b ~ + ∑ i = 1 n s i a ~ i ⋅ v ˉ ) ⏟ = G L W E ‾ s ′ ( X − μ ~ ∗ ⋅ v ˉ ) ← G L W E ‾ s ′ ( u ˉ ) \bar{\mathfrak{c}}'\leftarrow \underbrace{\overline{GLWE}_{\mathfrak{s}'}(X^{-\tilde{b}+\sum_{i=1}^{n}s_i\tilde{a}_i}\cdot \bar{v})}_{=\overline{GLWE}_{\mathfrak{s}'}(X^{-\tilde{\mu}^*}\cdot \bar{v})}\\ \leftarrow \overline{GLWE}_{\mathfrak{s}'}(\bar{u}) cˉ′←=GLWEs′(X−μ~∗⋅vˉ) GLWEs′(X−b~+∑i=1nsia~i⋅vˉ)←GLWEs′(uˉ)
其中,多项式 u ˉ ∈ Z ^ N [ X ] \bar{u}\in\hat{\mathbb{Z}}_N[X] uˉ∈Z^N[X]的常量项为 μ ˉ \bar{\mu} μˉ,即 u ˉ : = X − μ ~ ∗ ⋅ v ˉ = u ˉ 0 + u ˉ 1 X + ⋯ + u ˉ N − 1 X N − 1 \bar{u}:=X^{-\tilde{\mu}^*}\cdot \bar{v}=\bar{u}_0+\bar{u}_1X+\cdots+\bar{u}_{N-1}X^{N-1} uˉ:=X−μ~∗⋅vˉ=uˉ0+uˉ1X+⋯+uˉN−1XN−1,其中 u ˉ 0 = μ ˉ \bar{u}_0=\bar{\mu} uˉ0=μˉ。
bootstrapping剩余的步骤包含:
- sample extraction:
- 提取 u ˉ = X − μ ~ ∗ ⋅ v ˉ \bar{u}=X^{-\tilde{\mu}^*}\cdot \bar{v} uˉ=X−μ~∗⋅vˉ 作为 μ ˉ \bar{\mu} μˉ的 L W E ‾ \overline{LWE} LWE密文。
- 其实际是简单的提取 c ˉ ′ \bar{\mathfrak{c}}' cˉ′ G L W E ‾ \overline{GLWE} GLWE密文 中的一些系数。
sample extraction的实现细节为:
- 1)令 s ′ = ( s 1 ′ , ⋯ , s k ′ ) ∈ B N [ X ] k \mathfrak{s}'=(\mathfrak{s}'_1,\cdots,\mathfrak{s}'_k)\in\mathbb{B}_N[X]^k s′=(s1′,⋯,sk′)∈BN[X]k,其中对于 1 ≤ j ≤ k 1\leq j\leq k 1≤j≤k,有:
s j ′ = s j , 0 ′ + ⋯ + s j , N − 1 ′ X N − 1 \mathfrak{s}'_j=s_{j,0}'+\cdots +s_{j,N-1}'X^{N-1} sj′=sj,0′+⋯+sj,N−1′XN−1 - 2)将 c ˉ ′ ← G L W E ‾ s ′ ( u ˉ ) ∈ Z ^ N [ X ] k + 1 \bar{\mathfrak{c}}' \leftarrow \overline{GLWE}_{\mathfrak{s}'}(\bar{u})\in\hat{\mathbb{Z}}_N[X]^{k+1} cˉ′←GLWEs′(uˉ)∈Z^N[X]k+1解析为 ( a ˉ 1 ′ , ⋯ , a ˉ k ′ , b ˉ ′ ) (\bar{\mathfrak{a}}_1',\cdots,\bar{\mathfrak{a}}_k',\bar{\mathfrak{b}}') (aˉ1′,⋯,aˉk′,bˉ′),其中对于 1 ≤ j ≤ k 1\leq j\leq k 1≤j≤k,有:
a ˉ j ′ = a ˉ j , 0 ′ + ⋯ + a ˉ j , N − 1 ′ X N − 1 \bar{\mathfrak{a}}_j'=\bar{a}_{j,0}'+\cdots+\bar{a}_{j,N-1}'X^{N-1} aˉj′=aˉj,0′+⋯+aˉj,N−1′XN−1
b ˉ ′ = b ˉ 0 ′ + ⋯ + b ˉ N − 1 ′ X N − 1 \bar{\mathfrak{b}}'=\bar{b}_{0}'+\cdots+\bar{b}_{N-1}'X^{N-1} bˉ′=bˉ0′+⋯+bˉN−1′XN−1 - 3)可验证, c ˉ ′ : = ( a ˉ 1 , 0 ′ , − a ˉ 1 , N − 1 ′ , ⋯ , − a ˉ 1 , 1 ′ , ⋯ , a ˉ k , 0 ′ , − a ˉ k , N − 1 ′ , − a ˉ k , 1 ′ , b ˉ 0 ′ ) ∈ ( Z / q Z ) k N + 1 \bar{c}':=(\bar{a}_{1,0}',-\bar{a}_{1,N-1}',\cdots,-\bar{a}_{1,1}',\cdots,\bar{a}_{k,0}',-\bar{a}_{k,N-1}',-\bar{a}_{k,1}',\bar{b}_0')\in(\mathbb{Z}/q\mathbb{Z})^{kN+1} cˉ′:=(aˉ1,0′,−aˉ1,N−1′,⋯,−aˉ1,1′,⋯,aˉk,0′,−aˉk,N−1′,−aˉk,1′,bˉ0′)∈(Z/qZ)kN+1,为,基于key s ′ = ( s 1 ′ , ⋯ , s k N ′ ) ∈ B k N \mathbf{s}'=(s_1',\cdots,s'_{kN})\in\mathbb{B}^{kN} s′=(s1′,⋯,skN′)∈BkN,对 μ ˉ \bar{\mu} μˉ的 L W E ‾ \overline{LWE} LWE加密。其中对于 1 ≤ j ≤ k 1\leq j\leq k 1≤j≤k和 0 ≤ l ≤ N − 1 0\leq l\leq N-1 0≤l≤N−1,有 s l + 1 + ( j − 1 ) N ′ : = s j , l ′ s'_{l+1+(j-1)N}:=s'_{j,l} sl+1+(j−1)N′:=sj,l′。
4.1.3 key switching
经以上blind rotation和sample extraction之后,会将输入密文 c ˉ ← L W E ‾ s ( μ ˉ ) ∈ ( Z / q Z ) n + 1 \bar{c}\leftarrow\overline{LWE}_{\mathbf{s}}(\bar{\mu})\in(\mathbb{Z}/q\mathbb{Z})^{n+1} cˉ←LWEs(μˉ)∈(Z/qZ)n+1,转换为输出密文 c ˉ ′ ← L W E ‾ s ′ ( μ ˉ ) ∈ ( Z / q Z ) n + 1 \bar{c}'\leftarrow\overline{LWE}_{\mathbf{s}'}(\bar{\mu})\in(\mathbb{Z}/q\mathbb{Z})^{n+1} cˉ′←LWEs′(μˉ)∈(Z/qZ)n+1,二者加密的是相同的明文 μ ˉ \bar{\mu} μˉ,但使用的是不同的加密密钥,且具有不同的格式。
为将 c ˉ ′ \bar{c}' cˉ′转换为原始的 c ˉ \bar{c} cˉ,需要额外的操作:
- key switching
FHE中,key switching是经典技术,可用于:
- 在不同的参数设置下,对加密密钥进行switch。
实现key switching技术时,需用到key-switching keys。所谓key-switching keys,其本质为:
理论上看,key switching看起来与bootstrapping非常相似:
- bootstrapping:降低噪声,以满足计算要求。
- key switching:增加噪声,使得evaluate更便宜。
Remark 2:
如上所属,输入明文会经过3个转换:
- 1)blind rotation:有噪声的
- 2)sample extraction:无噪声的
- 3)key switching:有噪声的
c ˉ ( o u t ) ← K e y S w i t c h ∘ S a m p l e E x t r a c t ∘ B l i n d R o t a t e ( c ˉ ( i n ) ) \bar{c}^{(out)}\leftarrow KeySwitch \circ SampleExtract \circ BlindRotate (\bar{c}^{(in)}) cˉ(out)←KeySwitch∘SampleExtract∘BlindRotate(cˉ(in))

同时,在Florian Bourse等人2018年论文 Fast homomorphic evaluation of deep discretized neural networks中,作者发现,[nosiy] key switching流程可四处移动。
考虑到输入输出密文均属于 ( Z / q Z ) k N + 1 (\mathbb{Z}/q\mathbb{Z})^{kN+1} (Z/qZ)kN+1,则bootstrapping流程也可表示为:
c ˉ ′ ( o u t ) ← S a m p l e E x t r a c t ∘ B l i n d R o t a t e ∘ K e y S w i t c h ( c ˉ ′ ( i n ) ) \bar{c}'^{(out)}\leftarrow SampleExtract \circ BlindRotate \circ KeySwitch (\bar{c}'^{(in)}) cˉ′(out)←SampleExtract∘BlindRotate∘KeySwitch(cˉ′(in))
由于sample extraction是无噪声的,输出密文中包含的唯一噪声源自blind rotation。与key switching相对应的噪声不会相加。
4.2 Look-up Table Evaluation
之前章节中,blind rotation用于做bootstrapping。
此外,blind rotation技术还可调整用于对函数evaluate。函数会被evaluate为某编码进test polynomial的look-up table。
特别地,对于具有domain D \mathscr{D} D的任意函数 f f f,基于已加密数据进行evaluate,并想象有 F \mathscr{F} F:
f : D → F , x ↦ y = f ( x ) f:\mathscr{D}\rightarrow \mathscr{F},x\mapsto y=f(x) f:D→F,x↦y=f(x)。
假设已知编码函数 E n c o d e : D → Z / q Z Encode: \mathscr{D}\rightarrow \mathbb{Z}/q\mathbb{Z} Encode:D→Z/qZ 和 E n c o d e ′ : F → Z / q Z Encode': \mathscr{F}\rightarrow \mathbb{Z}/q\mathbb{Z} Encode′:F→Z/qZ,及其相应的解码函数 D e c o d e Decode Decode 和 D e c o d e ′ Decode' Decode′。
之前章节中提到,通过选择test polynomail v ˉ = v ˉ 0 + v ˉ 1 X + ⋯ + v ˉ N − 1 X N − 1 \bar{v}=\bar{v}_0+\bar{v}_1X+\cdots+\bar{v}_{N-1}X^{N-1} vˉ=vˉ0+vˉ1X+⋯+vˉN−1XN−1,其中 v ˉ i = U p p e r q , p ( q 2 N i m o d q ) \bar{v}_i=Upper_{q,p}(\frac{q}{2N}i\mod q) vˉi=Upperq,p(2Nqimodq),可将某 μ ˉ \bar{\mu} μˉ的密文,转换为具有更低噪声的、对相同 μ ˉ \bar{\mu} μˉ的密文。
对于 0 ≤ i ≤ N − 1 0\leq i \leq N-1 0≤i≤N−1,定义具有pairs ( i , T [ i ] ) (i,T[i]) (i,T[i])的look-up table,其中:
T [ i ] = E n c o d e ′ ∘ f ∘ D e c o d e ∘ U p p e r q , p ( q 2 N i m o d q ) T[i]=Encode' \circ f\circ Decode\circ Upper_{q,p}(\frac{q}{2N}i\mod q) T[i]=Encode′∘f∘Decode∘Upperq,p(2Nqimodq)

如上图所示,有test polynomail v ˉ = v ˉ 0 + v ˉ 1 X + ⋯ + v ˉ N − 1 X N − 1 \bar{v}=\bar{v}_0+\bar{v}_1X+\cdots+\bar{v}_{N-1}X^{N-1} vˉ=vˉ0+vˉ1X+⋯+vˉN−1XN−1,其中 v ˉ i = T [ i ] \bar{v}_i=T[i] vˉi=T[i]。剩下的处理流程与4.1节中的一致,保持不变。
这样,up to the drift, μ ˉ \bar{\mu} μˉ的输入密文( μ ˉ \bar{\mu} μˉ为对某 s ∈ D s\in\mathscr{D} s∈D值的编码),将被转换为编码了 f ( x ) f(x) f(x)值的密文。此外,作为bootstrapping的输出,最终的密文具有低级别的噪声。以上整个流程称为programmable bootstrapping。
Remark 3:
- 常规的bootstrapping,要求编码参数 w ˉ ≥ 1 \bar{w}\geq 1 wˉ≥1。
- 当look-up table中的元素是negacyclic时,可将常规bootstrapping提升为programmable bootstrapping。所谓negacyclic,是指 T [ i + N ] ≡ − T [ i ] ( m o d 2 N ) T[i+N]\equiv -T[i](\mod 2N) T[i+N]≡−T[i](mod2N),此时 2 N 2N 2N值实际是programmed。
5. 神经网络应用
至此,所有工具均已列出。本节,将把这些工具用于对神经网络进行同态evaluate。
Neural Network(NN,神经网络)最初是在计算机科学中通过类比人脑来构建的,目的是解决机器以前无法解决的复杂问题。神经网络可以被训练,然后用于对物体进行分类、探测疾病、进行人脸识别等。神经网络如下图所示,由相互连接的人工神经元组成,这些神经元会分层:
- 第一层包含初始数据,称为输入层。
- 最后一层称为输出层。
- 输入层与输出层之间的层用于计算,称为hidden隐藏层。

如下图展示了单个人工神经元示例结构。人工神经元模仿生物神经元。神经元接收: - d d d个输入信号 x i x_i xi,每个信号由参数 w i w_i wi(量化其各自的影响)加权
- 1个输入偏置参数$b。
- 输出信号为 z = f ( s ) z=f(s) z=f(s),其中 s = ∑ d i = w i x i + b s=\sum_d^i=w_i x_i+b s=∑di=wixi+b。函数 f f f是非线性的,并被称为激活函数。
神经网络中的不同层通常旨在从输入数据中连续提取辨别特征或模式。层的数量和在每层中执行的操作类型取决于神经网络试图实现的任务。
接下来回顾一些常用于构建神经网络的层。该清单并非详尽无遗。本文技术是通用的,支持所有已知类型的层。每个层接收来自前一层的输入,执行一些计算,并产生输出。输出然后作为输入流到下一层。在处理加密数据时,可以区分两种类型的层:
- 1)可使用分级运算(leveled operations)进行同态评估的层;【只要噪声超过某个阈值,第一类型的层也可以对一些中间值进行自举操作。】
- 2)涉及非线性或更复杂操作的层,在这种情况下,需要一个或多个可编程自举(PBS,Programmable bootstrappings)。
5.1 没有PBS的层
没有PBS的层有:
- 1)Dense/linear密集/线性层
- 2)convolution卷积层
- 3)addition加法层
- 4)Flatten拍平层
- 5)Global average pooling全局平均池化层
5.1.1 Dense/linear致密/线性层
(全连接)密集层,计算输入和权重矩阵之间的点积。可添加一个偏置向量。激活函数然后按逐个元素应用以产生输出。当没有激活函数时,密集层也称为线性层。
当以同态方式进行评估时,权重和偏置向量是明文停工的。因此,对密集层(激活除外)的评估包括一系列常数乘法和加法运算,这些运算都是leveled operations。
激活函数将在下一节中进行处理(请参见激活层)。
5.1.2 convolution卷积层
卷积层将输入层与由权重张量组成的卷积核(也称为filters滤波器)进行卷积,以产生输出张量。可以将偏差添加到输出中。此外,激活函数可以应用于输出。下图一个2D卷积。

filters是明文提供的。与密集层类似,对卷积层(激活除外)的评估包括一系列常数乘法和加法运算,这些运算都是leveled operations。
5.1.3 addition加法层
加法层会逐元素做加法运算。基于已加密数据,这些都是leveled operations。
5.1.4 Flatten拍平层
拍平层,会将输入,重整为低维度数组——如,喂入随后的密基层。
基于已加密数据,拍平函数简单地对输入密文进行重排。无需同态运算。
5.1.5 Global average pooling全局平均池化层
全局平均池化层,计算输入元素的平均值。若 n n n表示元素个数, a i a_i ai表示第 i i i个元素的值,则全局平均池化函数计算:
( ∑ i = 1 n a i ) / n (\sum_{i=1}^{n}a_i)/n (∑i=1nai)/n
在同态评估时,可将全局平均池化reduce为求和计算 ∑ i = 1 n a i \sum_{i=1}^{n}a_i ∑i=1nai。除以 n n n的运算可在后续programmable bootstrapping中进行——如在密集层或卷积层中,除以相同量的权重。因此,对全局平均池化层同态评估时,仅需要做密文加法运算——是leveled operations。
5.2 具有PBS的层
具有PBS的层有:
- 1)激活层:ReLU
- 2)最大池化层
5.2.1 激活层:ReLU
激活层,用于向神经网络中注入非线性性。在学习中,激活层至关重要。激活层中可使用很多激活函数。最流行的激活函数为:
其它常用的激活函数有:
- sigmoid函数
- hyperbolic tangent函数
如第4章所属,对激活函数(即任意函数)的同态评估,可通过programmable bootstrapping(PBS)来实现,该函数的输出编码在test polynomials内。
5.2.2 最大池化层
最大池化层,从输入中提取固定大小的元素子集,并计算其中的最大值。
初步看,max函数是多变量的(其对输入有多个参数),如何对其同态评估是并不清晰的。
通过2个参数,max函数可表示为【单变量】ReLU函数:
max ( x , y ) = y + R e L U ( x − y ) \max(x,y)=y+ReLU(x-y) max(x,y)=y+ReLU(x−y)
因此,通过密文 E n c r y p t ( x ) , E n c r y p t ( y ) Encrypt(x),Encrypt(y) Encrypt(x),Encrypt(y),有 E n c r y p t ( max ( x , y ) ) = E n c r y p t ( y ) + E n c r y p t ( R e L U ( z ) ) Encrypt(\max(x,y))=Encrypt(y)+Encrypt(ReLU(z)) Encrypt(max(x,y))=Encrypt(y)+Encrypt(ReLU(z)),其中 E n c r y p t ( z ) = E n c r y p t ( x ) − E n c r y p t ( y ) Encrypt(z)=Encrypt(x)-Encrypt(y) Encrypt(z)=Encrypt(x)−Encrypt(y)。这需要一组密文加减法,以及对ReLU函数的同态评估,对应的开销为one PBS。
为对具有更多参数的最大池化层进行评估,基本的关系为:
- max ( x , ⋯ , x k − 1 , x k ) = max ( y k , x k ) \max(x_,\cdots,x_{k-1},x_k)=\max(y_k,x_k) max(x,⋯,xk−1,xk)=max(yk,xk),其中:
- y k = max ( x , ⋯ , x k − 1 ) y_k=\max(x_,\cdots,x_{k-1}) yk=max(x,⋯,xk−1),以此类推。
对 k k k个元素 ( x 1 , ⋯ , x k ) (x_1,\cdots,x_k) (x1,⋯,xk)的最大池化函数进行同态评估,需要 k − 1 k-1 k−1个PBS。
6. 试验结果和benchmarks
本文进行了一系列试验以评估性能。基于MNIST数据集——其包含了手写数字的 28 × 28 28\times 28 28×28图片。为测试需要,设计了depth为20、50、100的神经网络,分别表示为 N N − 20 NN-20 NN−20、 N N − 50 NN-50 NN−50、 N N − 100 NN-100 NN−100。这些网络均包含了具有激活函数的密集层和卷积层,且每个隐藏层至少拥有92个活跃神经元。
6.1 parameter sets参数集
目标安全级别为80位和128位。word-size为 Ω = 64 \Omega=64 Ω=64位。针对 G L W E ‾ \overline{GLWE} GLWE加密的 ( k , N , σ ) (k,N,\sigma) (k,N,σ)参数,以及, L W E ‾ \overline{LWE} LWE加密的 ( n , σ ) (n,\sigma) (n,σ)参数为:

不同的参数集Ⅰ、Ⅱ、Ⅲ,均至少满足所声称的安全级别,且均使用lwe-estimator验证。这些参数集可用于最大精度为8位到12位的同态推理网络。
6.2 性能分析
性能测试时,主要针对2类不同机器:
- PC个人电脑: 2.6 GHz 6-Core Intel® Core™ i7处理器
- AWS云服务器:3.00 GHz Intel® Xeon® Platinum 8275CL processor with 96 vCPUs
下图Table 2中:
下图Table 3中:
- run-time和accuracy是针对已加密数据推理的。
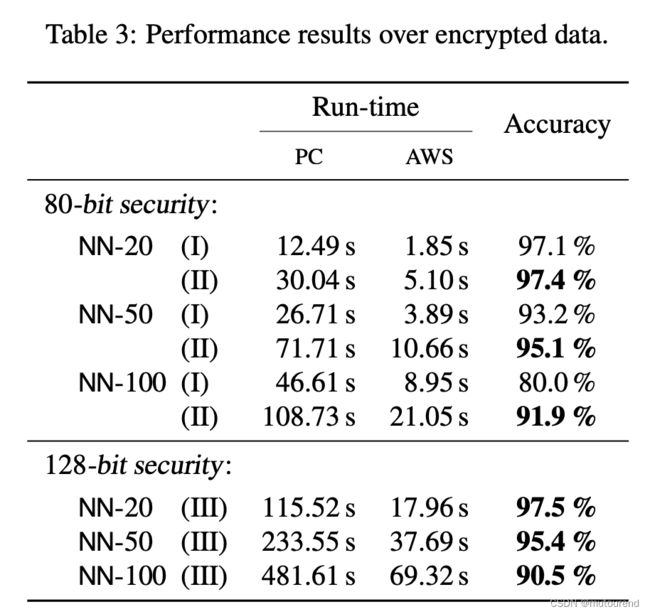
Table 3中结论,明确说明了参数选择的重要性,以及不同的取舍权衡。特别地,参数 N N N值越大,将增加accuracy,代价是更多的processing(即run-time)。
7. 结论
本文提出了一个使用全同态加密评估深度神经网络的通用框架。本文方法可有效地根据层数进行缩放,同时提供良好的精度结果。为此,采用了编码方法和可编程自举技术的通用组合。据已知信息,本文结果在深度神经网络的同态推理中创下了新纪录。
本文框架的实用性需要进一步的研究:
- 首先,了解在本文框架中使用专用硬件的影响是很有意思的。作者认为,通过这种方式可将处理时长提升几个数量级。
- 另一项有趣的工作是研究如何将本文技术扩展到神经网络的同态训练,或者更广泛地扩展到其他密集的机器学习任务。
FHE系列博客
- 技术探秘:在RISC Zero中验证FHE——由隐藏到证明:FHE验证的ZK路径(1)
- 基于[Discretized] Torus的全同态加密指引(1)
- 基于[Discretized] Torus的全同态加密指引(2)
- TFHE——基于[Discretized] Torus的全同态加密 代码解析
- 技术探秘:在RISC Zero中验证FHE——RISC Zero应用的DevOps(2)
- FHE简介
- Zama TFHE-rs
- Zama TFHE-rs白皮书(1)


