数据结构大作业:散列法电话号码查找
有偿分享程序源码和设计报告(.docx格式)
- 一、课题描述
- 二、需求分析
- 三、概要设计
-
- 3.1 数据逻辑结构、存储结构分析
-
- 3.1.1开放地址哈希表(stuA)
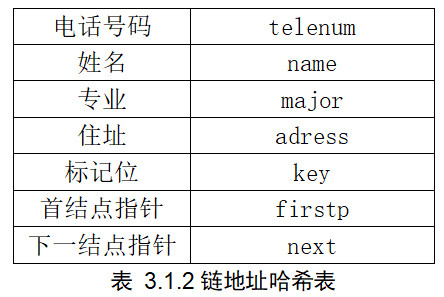
- 3.1.2链地址哈希表(chaining)
- 3.1.3用户输入电话号码结构体(input_callnumber)
- 3.2 程序设计图形展示
-
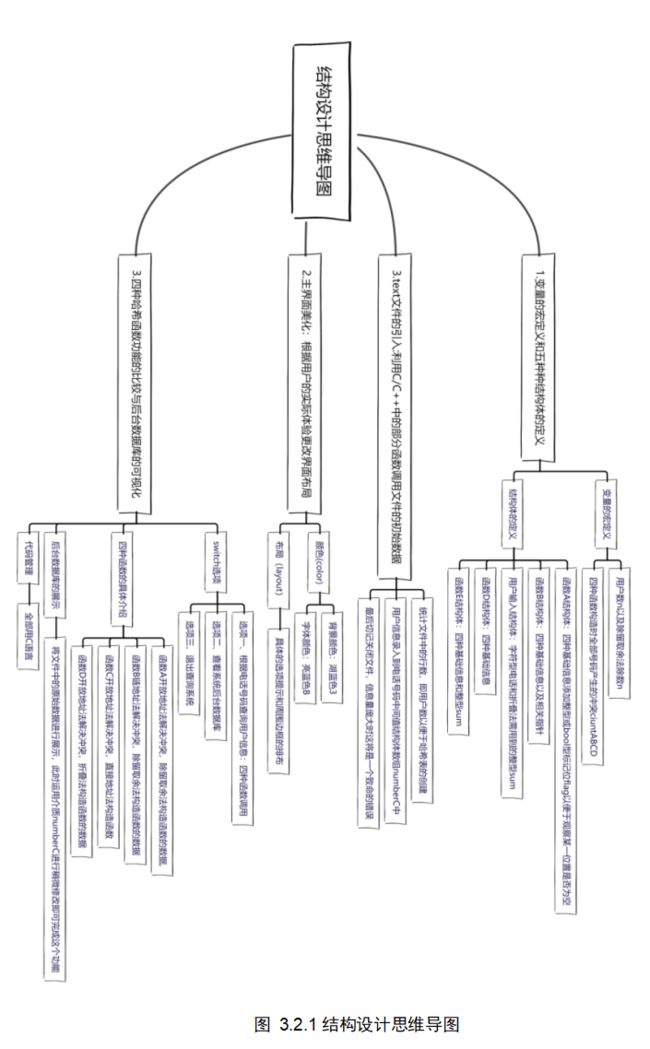
- 3.2.1 结构设计思维导图
- 3.2.2 程序流程图
- 3.3 程序结构及功能
-
- 3.3.1 一个主程序
- 3.3.2 六个子程序
-
- 3.3.2.1 美化界面beauty()
- 3.3.2.2 导入数据Statistics()
- 3.3.2.3 开放地址法 + 除留取余 Open()
- 3.3.2.4 开放地址法+ 折叠法folding()
- 3.3.2.5 开放地址法 + 直接地址direct()
- 3.3.2.6 链地址发解决冲突chaining()
- 四、详细设计
-
- 4.1 导入数据Statistics()
- 4.2 开放地址法 + 除留取余 Open()
- 4.3 开放地址法+ 折叠法folding()
- 4.4 开放地址法 + 直接地址direct()
- 4.5 链地址发解决冲突chaining()
- 五、测试数据及结果
-
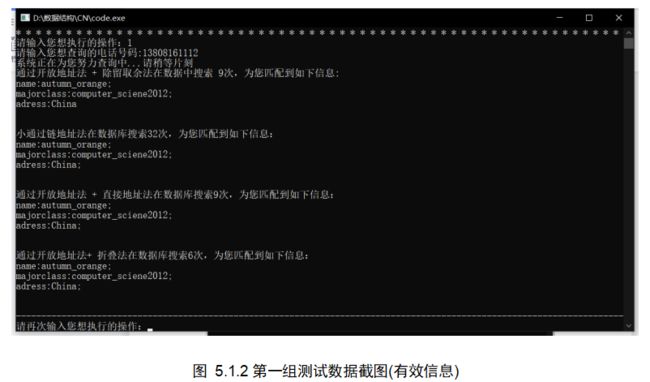
- 5.1按照电话号码查询用户信息
- 5.2数据统计模块
- 5.3算法设计模块
- 六、调试分析及总结
-
- 6.1调试过程中遇到的问题以及解决的方法描述
- 6.2 收获体会
一、课题描述
通过电话号码快速找出用户的信息。用户信息包括:手机号、姓名、班级、专业、住址等。
二、需求分析
用户数据信息包括电话号码、姓名、专业、住址等。软件需要实现以下功能:
(1)通过文件录入30个以上手机号开头为1380816的用户信息;能通过学号查询成绩;
(2)设计散列函数,以电话号码为关键字建立散列表;能统计每门被选课程的平均成绩;
(3)采用一定的方法解决冲突;
(4)显示每个电话号码的查询次数;
(5)能通过电话号码的查询用户其他的信息;
(6)要求设计两种以上散列函数,比较采用不同散列函数时全部号码的冲突次数。
三、概要设计
3.1 数据逻辑结构、存储结构分析
3.1.1开放地址哈希表(stuA)
3.1.2链地址哈希表(chaining)
3.1.3用户输入电话号码结构体(input_callnumber)
代码如下
typedef struct user_open
{
char telenum[maxn]; //电话号码
int sum;
char name[maxn]; //姓名
char major[maxn]; //专业
char adress[maxn]; //住址
int key;//标记位(若flag=false,则此处无数据。反之,则有。)
}stuA;
//单链表结点类型
typedef struct userB
{
char telenum[maxn];
int sum; //电话号码(telenumber)
char name[maxn];//姓名(name)
char major[maxn];//专业(major)
char adress[maxn];//住址(adress)
struct userB *next;//下一个结点指针 (node)
}spot;
typedef struct userb
{
spot *firstp; //首结点指针
}stuB;
//用户输入的电话号码
typedef struct input_callnumber
{
char number[maxn]; //用户输入的电话号码
int sum;
}icn;
以字符存储电话号码,存储上可以采用顺序、链式存储(结构体数组结构体链表),初始数据和结果数据采用文本文件(.txt)来保存。
也可以全部数据用一个结构体,但会造成很多冗余(重复)存储的数据,浪费存储空间。
3.2 程序设计图形展示
3.2.1 结构设计思维导图
3.2.2 程序流程图
3.3 程序结构及功能
3.3.1 一个主程序
主函数main的选项操作:
①根据电话号码查询用户信息,输入号码查询时的错误提示,利用goto即可解决问题(如少于13位,有字符)。
②查看系统后台数据。
③退出系统。
3.3.2 六个子程序
3.3.2.1 美化界面beauty()
(1)主题界面美化beauty()根据用户的实际体验更改界面布局
int main()
{
int choice;
FORWORD:
scanf("%d", &choice);
switch(choice)
{
case 1:
while(1)
{
flag=1;
printf("请输入您想查询的电话号码(1380816开头)\n");
scanf("%s",telenumber.number);
if(strlen(telenumber.number)<11)
{
printf("您输入的号码长度不足11位,请重新输入\n");
continue;
}
if(strlen(telenumber.number)>11)
{
printf("您输入的号码长度超过11位,请重新输入\n");
continue;
}
for(int i=0;i<strlen(telenumber.number);i++)
{
if('9'<telenumber.number[i]||telenumber.number[i]<'0')
{
flag=0;
}
}
if(flag==0)
{
printf("您输入的号码含有非法字符,请重新输入\n");
}
if(strlen(telenumber.number)==11&&flag==1)
{
break;
}
}
printf("系统正在为您努力查询中...请稍等片刻\n");
Creat_Open();
Search_Open();
Creat_Chaining();
Search_Chaining();
Creat_direct();
Search_direct();
Creat_folding();
Search_folding();
printf("------------------------------------------------------------------------------------------------------------------------");
printf("请再次输入您想执行的操作:");
goto FORWORD;
break;
case 2:
for(int i=0;i<n;i++)
{
printf("%s %s %s %s", numberC[i].telenum,numberC[i].name, numberC[i].major, numberC[i].adress);
}
printf("\nA全部号码冲突次数:%d\nB全部号码冲突次数:%d\nD全部号码冲突次数:%d\nE号码全部冲突次数:%d\n",countA, countB, countD, countE);
printf("\n\n------------------------------------------------------------------------------------------------------------------------");
printf("请再次输入您想执行的操作:\n");
goto FORWORD;
break;
case 3: printf("谢谢您使用本系统,\n\n再见\n");return 0;
default:
printf("您输入的操作系统暂时不支持,请再次输入您想执行的操作:");
goto FORWORD;} }
3.3.2.2 导入数据Statistics()
参数描述:n统计文件中的函数,numberC[maxn]来存储经过线性变化 后的初始数据,ch读取文件中的每一个字符;
功能描述:①初步分析统计原始文件并将其导入至媒介数组。
3.3.2.3 开放地址法 + 除留取余 Open()
参数描述:adr为哈希函数值,countA为函数A的全部号码冲突次数,key为标记位,判断该位置受否为空(空为0,非空为1),每次操作都得将其置为1,count为查询冲突次数,countA为构造全部号码时的冲突次数。
功能描述:①将媒介numberC[maxn]进行初步变换导入到numberA[maxn]中。②在构造好的哈希表电话簿中查找电话。
3.3.2.4 开放地址法+ 折叠法folding()
参数描述:adr为哈希函数值,countE为函数A的全部号码冲突次数,key为标记位,判断该位置受否为空(空为0,非空为1),每次操作都得将其置为1,count为查询冲突次数,countE为构造全部号码时的冲突次数。
功能描述:①将numberC[maxn]初步变化后导入numberC[maxn]中。②在哈希表E中寻找该号码。
3.3.2.5 开放地址法 + 直接地址direct()
参数描述:countd为查询冲突次数,k记录是否被找到
功能描述:①将numberC[maxn]直接导入D表中。②在哈希表中查找该号码
3.3.2.6 链地址发解决冲突chaining()
参数描述:adr为哈希函数值,countB为函数B的全部号码冲突次数,count为查询冲突次数,countB为构造全部号码时的冲突次数,结构体指针q为媒介,利用他来实现链表的创建与遍历。
功能描述:①将媒介numberC[maxn]进行初步变换导入到numberA[maxn]中。②在哈希链表中进行查找号码
四、详细设计
4.1 导入数据Statistics()
①初步分析统计原始文件并将其导入至媒介数组,运用fscanf函数进行字符串的导入,以及ch的逐个读取判断文本的行数;
时间复杂度为(n),无需额外空间。
//从文件中导入初始文本数据:统计文件中的用户数
void Statistics_Users()
{
char ch;
FILE *input_file;
if((input_file=fopen("info.txt","rb+"))==NULL)
{
printf("Can not open the file!\n");
exit(0);
}
while(!feof(input_file))
{
ch=fgetc(input_file);//从txt文本中读取一个字符赋值给ch
if(ch=='\n') //如果这个字符为换行符
n++;
}
fclose(input_file);
}
//从文件中导入初始文本数据:将用户信息录入到电话号码顺序表中
void Statistics_sequential()
{
FILE *input_file;
if((input_file=fopen("info.txt","rb+"))==NULL)
{
printf("Can not open the file!\n");
exit(0);
}
for(int i=0;i<n;i++)
{
fscanf(input_file,"%[^,],%[^,],%[^,],%s",numberC[i].telenum,numberC[i].name,numberC[i].major,numberC[i].adress);
}
fclose(input_file);
}
4.2 开放地址法 + 除留取余 Open()
①将媒介numberC[maxn]进行初步变换导入到numberA[maxn]中,先将numberA[maxn]置空,判断key是否为空,空则直接导入,非空则寻找下一空位补齐。
②在构造好的哈希表电话簿中查找电话,先将电话号码取余,再在号码表中利用while寻找,判断两个号码的关键是号码后四位的是否相同,是就输出,否则while循环查找。
时间复杂度为(n),空间复杂度为(n)
void Creat_Open()
{
for(int i=0;i<n;i++)
{
numberA[i].key=0; //哈希表置空
}
int adr;
for(int i=0;i<n;i++) //0到n个用户依次存入A表中
{
adr=numberC[i].sum%m; //计算哈希函数值
if(numberA[adr].key==0) //若adr处无数据(无冲突)
{
strcpy(numberA[adr].telenum,numberC[i].telenum); //将第i个用户存入adr中
strcpy(numberA[adr].name,numberC[i].name);
strcpy(numberA[adr].major,numberC[i].major);
strcpy(numberA[adr].adress,numberC[i].adress);
numberA[adr].sum=numberC[i].sum;
numberA[adr].key=1; //标记其有数据
}
else //adr处有数据(有冲突)
{
while(numberA[adr].key!=0)
{
adr++;
countA++;
}
strcpy(numberA[adr].telenum,numberC[i].telenum); //将第i个用户存入adr中
strcpy(numberA[adr].name,numberC[i].name);
strcpy(numberA[adr].major,numberC[i].major);
strcpy(numberA[adr].adress,numberC[i].adress);
numberA[adr].sum=numberC[i].sum;
numberA[adr].key=1;
}
}
}
//通过电话号码本A查询信息查询
void Search_Open()
{
int count=1, adr;
adr=telenumber.sum%m;
if(numberA[adr].telenum[17]-'0'==telenumber.number[7]-'0'&&numberA[adr].telenum[18]-'0'==telenumber.number[8]-'0'&&numberA[adr].telenum[19]-'0'==telenumber.number[9]-'0'&&numberA[adr].telenum[20]-'0'==telenumber.number[10]-'0')
{
printf("通过开放地址法 + 除留取余法在数据中搜索 %d次,为您匹配到如下信息:\n%s;\n%s;\n%s\n",count , numberA[adr].name, numberA[adr].major, numberA[adr].adress);
printf("\n\n");
}
else
{
while(numberA[adr].telenum[17]-'0'!=telenumber.number[7]-'0'||numberA[adr].telenum[18]-'0'!=telenumber.number[8]-'0'||numberA[adr].telenum[19]-'0'!=telenumber.number[9]-'0'||numberA[adr].telenum[20]-'0'!=telenumber.number[10]-'0')
{
adr++;
count++;
if(count > n)
{
printf("开放地址法 + 除留取余法未在数据库中匹配到此电话号码\n");
printf("\n\n");
return ;
}
}
printf("通过开放地址法 + 除留取余法在数据中搜索%d次,为您匹配到如下信息:\n%s;\n%s;\n%s\n",count , numberA[adr].name, numberA[adr].major, numberA[adr].adress);
printf("\n\n");
}
}
4.3 开放地址法+ 折叠法folding()
①将numberC[maxn]初步变化后导入numberC[maxn]中,首先将哈希表key置空方便后面的判断,然后计算后四位号码之和存入sum中,再记录最后两位的值存入telenum中,判断adr=(sum)处是否有冲突,若adr处无数据(无冲突) ,将第i个用户存入adr中;adr处有数据(有冲突) ,相后寻找空位插入数据。
②在哈希表E中寻找该号码,寻找i=sum的值,判断是否最后两位相等,相等则输出数据,否则往后继续查找。
时间复杂度为(n),空间复杂度为(n^2),
void Creat_folding()
{
for(int i=0;i<n;i++)
{
numberE[i].key=0; //哈希表置空
}
int count=1, adr;
for(int i=0;i<n;i++) //为折叠法做前奏
{
numberC[i].sum=(numberC[i].telenum[17]-'0')+(numberC[i].telenum[18]-'0')+(numberC[i].telenum[19]-'0')+(numberC[i].telenum[20]-'0');
telenumber.sum=(telenumber.number[7]-'0')+(telenumber.number[8]-'0')+(telenumber.number[9]-'0')+(telenumber.number[10]-'0');
}
for(int i=0;i<n;i++)
{
adr=numberC[i].sum;
if(numberE[adr].key==0) //若adr处无数据(无冲突)
{
strcpy(numberE[adr].telenum,numberC[i].telenum); //将第i个用户存入adr中
strcpy(numberE[adr].name,numberC[i].name);
strcpy(numberE[adr].major,numberC[i].major);
strcpy(numberE[adr].adress,numberC[i].adress);
numberE[adr].sum=numberC[i].sum;
numberE[adr].key=1; //标记其有数据
}
else //adr处有数据(有冲突)
{
while(numberE[adr].key!=0)
{
adr++;
count++;
}
strcpy(numberE[adr].telenum,numberC[i].telenum); //将第i个用户存入adr中
strcpy(numberE[adr].name,numberC[i].name);
strcpy(numberE[adr].major,numberC[i].major);
strcpy(numberE[adr].adress,numberC[i].adress);
numberE[adr].sum=numberC[i].sum;
numberE[adr].key=1;
}
}
countE=count;
}
void Search_folding()
{
int count=1,k=0;
for(int i=0;i<n;i++)
{
if(numberE[i].sum==telenumber.sum)
{
if(numberE[i].telenum[17]-'0'==telenumber.number[7]-'0'&&numberE[i].telenum[18]-'0'==telenumber.number[8]-'0'&&numberE[i].telenum[19]-'0'==telenumber.number[9]-'0'&&numberE[i].telenum[20]-'0'==telenumber.number[10]-'0')
{
printf("通过开放地址法+ 折叠法在数据库搜索%d次,为您匹配到如下信息:\n%s;\n%s;\n%s;\n\n\n", count, numberE[i].name, numberE[i].major, numberE[i].adress);
k=1;
}
}
else count++;
}
if(k==0) printf("开放地址法+ 折叠法未在数据库中未匹配到此电话号码\n\n");
}
4.4 开放地址法 + 直接地址direct()
①将numberC[maxn]直接导入D表中
②在哈希表中查找该号码时间复杂度为(n^2),空间复杂度为(n)
void Creat_direct()
{
int count;
for(int i=0;i<n;i++)
{
strcpy(numberD[i].telenum,numberC[i].telenum);
strcpy(numberD[i].name,numberC[i].name);
strcpy(numberD[i].major,numberC[i].major);
strcpy(numberD[i].adress,numberC[i].adress);
}
}
void Search_direct()
{
int countd=1, k=0;
for(int i=0;i<n;i++)
{
if(numberD[i].telenum[17]-'0'==telenumber.number[7]-'0'&&numberD[i].telenum[18]-'0'==telenumber.number[8]-'0'&&numberD[i].telenum[19]-'0'==telenumber.number[9]-'0'&&numberD[i].telenum[20]-'0'==telenumber.number[10]-'0')
{
printf("通过开放地址法 + 直接地址法在数据库搜索%d次,为您匹配到如下信息:\n%s;\n%s;\n%s;\n\n\n", countd, numberD[i].name, numberD[i].major, numberD[i].adress);
k=1;
}
else countd++;
}
if(k==0)
{
printf(开放地址法 + 直接地址法未在数据库中匹配到此电话号码\n\n");
}
}
4.5 链地址发解决冲突chaining()
①将媒介numberC[maxn]进行初步变换导入到numberA[maxn]中,将哈希表的firstp进行初始化,然后将0到n个用户利用for循环依次存入B表中,计算哈希函数值,创建一个结点存放学生信息,判断单链表是否为空,为空则将结点指针q链接放入数据,若非空则采用头插法插入到链表中。
②在哈希链表中进行查找号码,q指向对应单链表的首结点利用while扫描单链表adr的所有结点,找到就跳出循环结束程序。
时间复杂度(n), 空间复杂度(n)
void Creat_Chaining()
{
for(int i=0;i<n;i++) //哈希表的初始化
{
numberB[i].firstp=NULL;
}
int adr;
for(int i=0;i<n;i++) //0到n个用户依次存入B表中
{
adr=numberC[i].sum%m; //计算哈希函数值
spot *q;
q=(spot *)malloc(sizeof(spot));//创建一个结点存放学生信息
strcpy(q->telenum, numberC[i].telenum);
strcpy(q->name,numberC[i].name);
strcpy(q->major,numberC[i].major);
strcpy(q->adress,numberC[i].adress);
q->next=NULL;
if(numberB[adr].firstp==NULL) //若单链表为空
{
numberB[adr].firstp=q;
}
else //若单链表不为空
{
q->next=numberB[adr].firstp;//采用头插法插入到哈希表B单链表中
numberB[adr].firstp=q;
countB++;
}
}
}
//通过电话号码B查询信息查询
void Search_Chaining()
{
int count=1, adr;
adr=telenumber.sum%m;
spot *q;
q=numberB[adr].firstp; //q指向对应单链表的首结点
while(q!=NULL) //扫描单链表adr的所有结点
{
count++;
if(q->telenum[17]-'0'==telenumber.number[7]-'0'&&q->telenum[18]-'0'==telenumber.number[8]-'0'&&q->telenum[19]-'0'==telenumber.number[9]-'0'&&q->telenum[20]-'0'==telenumber.number[10]-'0') //查找成功则退出循环
{
break;
}
q=q->next;
}
if(q!=NULL)
{
printf("通过链地址法在数据库搜索%d次,为您匹配到如下信息:\n%s;\n%s;\n%s;\n\n\n", count, q->name,q->major,q->adress);
}
else
{
printf("链地址法未在数据库中匹配到此电话号码\n\n");
}
五、测试数据及结果
5.1按照电话号码查询用户信息
5.2数据统计模块

关于文件录入时的一些注意事项:
①读取文件时会读取到回车,并将其存储两个字符,所以第一行使用CN等值与其他行的首行两字符。
②利用英文逗号分割同一用户的不同信息,因为在文件引入时利用了读取“,”识别不同信息。
③利用下划线_代替空格,因为fscanf读取到空格或回车时会自动换行进行下一信息的读取导致身份信息出现紊乱。
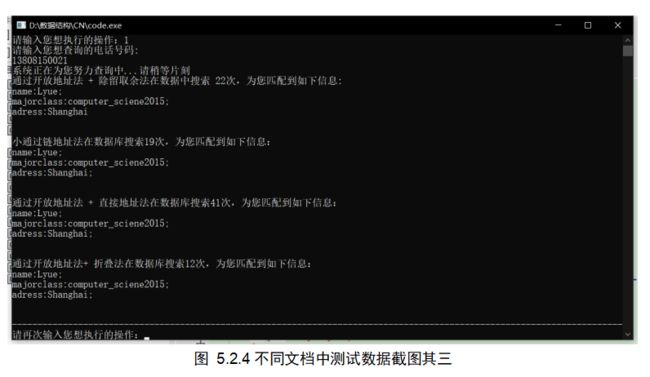
5.3算法设计模块
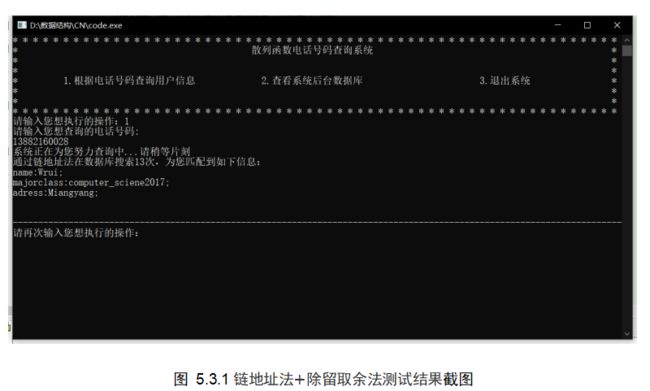
算法1 :链地址法+除留取余法
算法2 :开放地址法+除留取余法

算法3 : 开放地址法+直接地址法

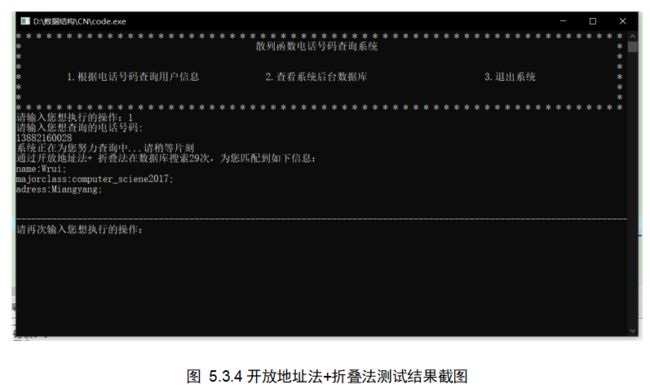
算法4 : 开放地址法+折叠法
总结 :
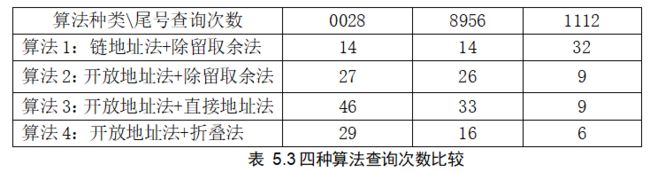
通过算法3和算法4的查询次数的比较得出折叠法的查询速度更快
通过算法2和算法4的查询次数比较得出折叠法与除留取余法相差不大
通过算法2和算法3的查询次数比较得出除留取余法的算法性能更高
通过算法1和算法2的查询次数比较得出链地址法解决冲突能提高算法性能
六、调试分析及总结
6.1调试过程中遇到的问题以及解决的方法描述
问题1:链地址法调试时发现所显示的变量为地址,不便于观察
问题截图:
问题解决方案:利用后台工具或者草图分析指针指向进行改正。
问题2:循环终止条件错误导致的电脑奔溃
调试截图:
问题解决方案:利用注释法逐步分析错误原因,逐行判断错误情况。
6.2 收获体会
此程序调试(debug)的具体步骤首先是设置断点,其次判断程序是否正常运行,然后判断当前变量是否符合预估条件,若符合就继续程序的运行直到找出错误为止,否则退出调试解决问题(比如循环终止条件的判断,指针指向异常等等情况)。以上方可同时采用printf()函数或将某些不必要的模块注释以便问题的查找。
调试时的几个注意点:
第一,调试时应当注意逻辑的或(||)与且(&&)是否有错误,这一步关系到号码查询时的次数,若处理不当严重时将会导致程序卡死在循环内导致电脑死机
第二,链地址法指针的指向问题,这一部分的调试只会显示地址导致数据不是非常的直观,建议利用画图工具或者纸质材料进行现场演算以找到错误原因。
宏定义的数据容量一定得足够大,否则数据库存放数据太多时将会导致程序奔溃,迟迟等不到运行结果。