模式识别与机器学习-SVM（线性支持向量机）

谨以此博客作为复习期间的记录

线性支持向量机

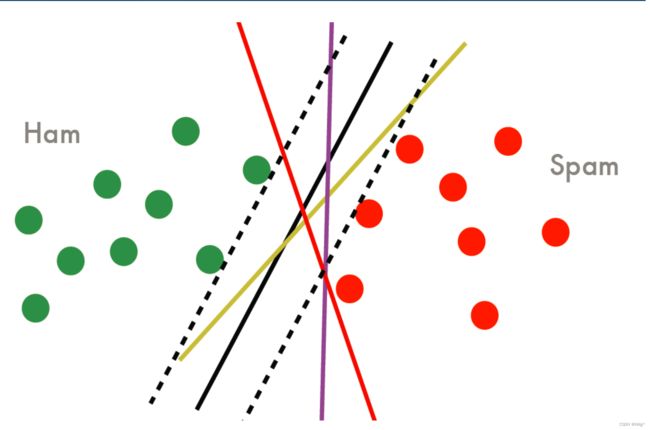
在以上四条线中，都可以作为分割平面，误差率也都为0。但是那个分割平面效果更好呢？其实可以看出，黑色的线具有更好的性质，因为如果将黑色的线作为分割平面，将会有更大的间隔距离。
其中，分割平面可以用以下式子表示:
$$wx+b=0$$
$w\text{和}b$都是有待学习的参数，SVM的核心思想之一就是找到这样的一个平面，使得间隔距离最大。那么该如何表述间隔距离呢？

间隔距离

在分割平面$wx+b=0$确定的情况下，对每一个样本点$x_i,|w{x}_i+b|$可以表示样本点$x_i$到分割平面的距离。而若是二分类，$y_i\in \{1,-1\}$，那么$y_i(w{x}_i+b)$同样可以表示样本点到分割平面的距离。

对于二分类问题，数据点 ${\mathbf{x}}_i$ 到超平面的函数间隔定义为：${\hat{\gamma }}_i=y_i(\mathbf{w}\cdot {\mathbf{x}}_i+b)$

函数间隔的正负号表示数据点所属的类别和超平面分割的一致性。当 ${\hat{\gamma }}_i>0$ 时，数据点 ${\mathbf{x}}_i$ 被正确地分类到超平面两侧的区域，而当 ${\hat{\gamma }}_i<0$ 时，数据点被错误地分类或位于超平面上。若 ${\hat{\gamma }}_i=0$，则表示数据点在超平面上。

而这里就可以得出SVM的初步思想:最大化最小函数间隔，公式表述如下
$$maxmin({\hat{\gamma }}_i)i=\mathrm{1...}N$$
也就是在所有样本点$(x_i,y_i)$中，可以找到离分割平面最近的点，我们想让这些点的距离达到最大。但是有一个问题，但是选择分离超平面时，只有函数间隔还不够．因为只要成比例地改变$w$和 $b$ ，例如将它们改为 $2w$ 和 $2b$ ，超平面并没有改变，但函数间隔却成为原来的 2 倍．这一事实启示我们，可以对分离超平面的法向量 $w$ 加某些约束，如规范化$||w||=1$,这时函数间隔就变为了几何间隔。
几何间隔 对于给定的训练数据集 $T$ 和超平面 $(w,b)$, 定义超平面 $(w,b)$ 关于样本点 $\left(x_i,y_i\right)$ 的几何间隔为
$${\gamma }_i=y_i\left(\frac{w}{\Vert w\Vert }\cdot x_i+\frac{b}{\Vert w\Vert }\right)$$

定义超平面 $(w,b)$ 关于训练数据集 $T$ 的几何间隔为超平面 $(w,b)$ 关于 $T$ 中所有样本点 $\left(x_i,y_i\right)$ 的几何间隔之最小值, 即
$$\gamma =\underset{i=1,\cdots ,N}{\min }{\gamma }_i$$

超平面 $(w,b)$ 关于样本点 $\left(x_i,y_i\right)$ 的几何间隔一般是实例点到超平面的带符号的距离 (signed distance), 当样本点被超平面正确分类时就是实例点到超平面的距离.

从函数间隔和几何间隔的定义 (式(7.3) 式(7.6)）可知, 函数间隔和几何间隔有下面的关系:
$$\begin{array}{c}{\gamma }_i=\frac{{\hat{\gamma }}_i}{\Vert w\Vert }\\ \gamma =\frac{\hat{\gamma }}{\Vert w\Vert }\end{array}$$

如果 $\Vert w\Vert =1$, 那么函数间隔和几何间隔相等. 如果超平面参数 $w$ 和 $b$ 成比例地改变 (超平面没有改变)，函数间隔也按此比例改变，而几何间隔不变.

那么，优化目标可以等价的表述如下
$$\begin{array}{rl}& \text{maximize}\gamma \\ & \text{subject to}\gamma \le y_i\left(\frac{\mathbf{w}}{\Vert \mathbf{w}\Vert }\cdot {\mathbf{x}}_i+\frac{b}{\Vert \mathbf{w}\Vert }\right),i=1,2,\dots ,n\end{array}$$
转化为几何间隔:

$$\begin{array}{rl}& \text{maximize}\frac{\hat{\gamma }}{\Vert w\Vert }\\ & \text{subject to}\hat{\gamma }\le y_i\left(\mathbf{w}\cdot {\mathbf{x}}_i+b\right),i=1,2,\dots ,n\end{array}$$
可以令$\hat{\gamma }=1$,目标函数变为$maximize\frac{1}{||w||}$,等价于$minimize\frac{1}{2}||w||$.原问题可化为以下形式.
$$\begin{array}{rl}& \text{minimize}\frac{1}{2}||w|{|}^2\\ & \text{subject to}{y}_i\left(\mathbf{w}\cdot {\mathbf{x}}_i+b\right)-1\ge 0,i=1,2,\dots ,n\end{array}$$
以上是一个凸优化问题，通过求解上述问题即可得到最终的最优决策平面。

在决定分离超平面时只有支持向量起作用，而其他实例点并不起作用．如果移动支持向量将改变所求的解；但是如果在间隔边界以外移动其他实例点，甚至去掉这些点，则解是不会改变的．由于支持向量在确定分离超平面中起着决定性作用，所以将这种分类模型称为支持向量机．支持向量的个数一般很少，所以支持向量机由很少的“重要的”训练样本确定．

学习的对偶算法

为了求解上述问题，可以构造拉格朗日函数，通过求解对偶问题得到原始问题的最优解。
这样做的优点，一是对偶问题往往更容易求解；二是自然引入核函数，进而推广到非线性分类问题。
首先构建拉格朗日函数 (Lagrange function). 为此, 对每一个不等式约束引进拉格朗日乘子 (Lagrange multiplier) ${\alpha }_i⩾0,i=1,2,\cdots ,N$, 定义拉格朗日函数:
$$L(w,b,\alpha )=\frac{1}{2}\Vert w{\Vert }^2-\sum _{i=1}^N{\alpha }_i{y}_i\left(w\cdot x_i+b\right)+\sum _{i=1}^N{\alpha }_i$$
其中, $\alpha ={\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_N\right)}^{\mathrm{T}}$ 为拉格朗日乘子向量.
根据拉格朗日对偶性，原始问题的对偶问题是极大极小问题:
$$\underset{\alpha }{\max }\underset{w,b}{\min }L(w,b,\alpha )$$

所以, 为了得到对偶问题的解, 需要先求 $L(w,b,\alpha )$ 对 $w,b$ 的极小, 再求对 $\alpha$ 的极大.

拉格朗日函数为：
$$L(w,b,\alpha )=\frac{1}{2}\Vert \mathbf{w}{\Vert }^2-\sum _{i=1}^N{\alpha }_i{y}_i(\mathbf{w}\cdot {\mathbf{x}}_i+b)+\sum _{i=1}^N{\alpha }_i$$

其中，$\alpha ={\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_N\right)}^{\mathrm{T}}$ 为拉格朗日乘子向量。

接下来，我们进行极小化 $L(w,b,\alpha )$ 对 $w$ 和 $b$的过程。需要对 $L(w,b,\alpha )$ 分别对 $w$ 和 $b$ 求偏导，并令其等于零：

对$w$ 的偏导数：
$\frac{\partial L}{\partial w}=w-{\sum }_{i=1}^N{\alpha }_i{y}_i{x}_i=0$
得到：$w={\sum }_{i=1}^N{\alpha }_i{y}_i{x}_i$

对 $b$ 的偏导数：
$\frac{\partial L}{\partial b}=-{\sum }_{i=1}^N{\alpha }_i{y}_i=0$
得到：${\sum }_{i=1}^N{\alpha }_i{y}_i=0$

将上述对 $w$ 和 $b$ 的结果代入拉格朗日函数 $L(w,b,\alpha )$，得到极小化后的结果

这样，对偶问题可以表示为：
$$\underset{\alpha }{\min }-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)+\sum _{i=1}^N{\alpha }_i$$
其中，${\alpha }_i⩾0$，$i=1,2,\cdots ,N$，并且满足 ${\sum }_{i=1}^N{\alpha }_i{y}_i=0$。
然后，对拉格朗日函数 $L(w,b,\alpha )$ 对 $\alpha$ 求极大值，这样就可以得到对偶问题的解。

那么求解得到$\alpha$之后，该如何反求出$w^{\ast },b^{\ast }$呢？
根据KKT条件，有
$$\begin{array}{rl}& {\nabla }_{w}L\left(w^{\ast },b^{\ast },{\alpha }^{\ast }\right)=w^{\ast }-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i=0\\ & {\nabla }_{b}L\left(w^{\ast },b^{\ast },{\alpha }^{\ast }\right)=-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i=0\\ & {\alpha }_i^{\ast }\left(y_i\left(w^{\ast }\cdot x_i+b^{\ast }\right)-1\right)=0,i=1,2,\cdots ,N\\ & y_i\left(w^{\ast }\cdot x_i+b^{\ast }\right)-1⩾0,i=1,2,\cdots ,N\\ & {\alpha }_i^{\ast }⩾0,i=1,2,\cdots ,N\end{array}$$
由此得
$$w^{\ast }=\sum _i{\alpha }_i^{\ast }{y}_i{x}_i$$
其中至少有一个 ${\alpha }_j^{\ast }>0$ (用反证法, 假设 ${\alpha }^{\ast }=0$, 由第一条KKT条件可知 $w^{\ast }=0$, 而 $w^{\ast }=0$不是原始最优化问题的解, 产生矛盾), 对此 $j$ 有
$$y_j\left(w^{\ast }\cdot x_j+b^{\ast }\right)-1=0$$
有$y_j^2=1$,$y_j\left(w^{\ast }\cdot x_j+b^{\ast }\right)-y_j^2=0$进而得出$w^{\ast }\cdot x_j+b^{\ast }-y_j=0$
因此，在求解出${\alpha }^{\ast }$之后，可以得到决策平面的$w^{\ast }和b^{\ast }$
$$\begin{gathered} w^{\ast }=\sum _i{\alpha }_i^{\ast }{y}_i{x}_i \\ {b}^{\ast }=y_j-w^{\ast }\cdot x_j \end{gathered}$$

算法:线性可分支持向量机学习算法

输入: 线性可分训练集 $T=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_N,y_N\right)\right\}$, 其中 $x_i\in \mathcal{X}={\mathbf{R}}^n,y_i\in$ $\mathcal{Y}=\{-1,+1\},i=1,2,\cdots ,N$;
输出: 分离超平面和分类决策函数.
（1）构造并求解约束最优化问题
$$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)-\sum _{i=1}^N{\alpha }_i\\ & \text{ s.t. }\sum _{i=1}^N{\alpha }_i{y}_i=0\\ & {\alpha }_i⩾0,i=1,2,\cdots ,N\end{array}$$

求得最优解 ${\alpha }^{\ast }={\left({\alpha }_1^{\ast },{\alpha }_2^{\ast },\cdots ,{\alpha }_N^{\ast }\right)}^{\mathrm{T}}$.
(2) 计算
$$w^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$$

并选择 ${\alpha }^{\ast }$ 的一个正分量 ${\alpha }_j^{\ast }>0$, 计算
$$b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i\left(x_i\cdot x_j\right)$$

(3) 求得分离超平面
$$w^{\ast }\cdot x+b^{\ast }=0$$

分类决策函数:
$$f(x)=\mathrm{sign}\left(w^{\ast }\cdot x+b^{\ast }\right)$$

在线性可分支持向量机中, $w^{\ast }$ 和 $b^{\ast }$ 只依赖于训练数据中对应于 ${\alpha }_i^{\ast }>0$ 的样本点 $\left(x_i,y_i\right)$, 而其他样本点对 $w^{\ast }$ 和 $b^{\ast }$ 没有影响. 我们将训练数据中对应于 ${\alpha }_i^{\ast }>0$ 的实例点 $x_i\in {\mathbf{R}}^n$ 称为支持向量.

线性可分支持向量机例子

带入
$$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)-\sum _{i=1}^N{\alpha }_i\\ & \text{ s.t. }\sum _{i=1}^N{\alpha }_i{y}_i=0\\ & {\alpha }_i⩾0,i=1,2,\cdots ,N\end{array}$$
解 根据所给数据, 对偶问题是
$$\begin{array}{ll}{\min }_{\alpha }& \frac{1}{2}{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)-{\sum }_{i=1}^N{\alpha }_i\\ & =\frac{1}{2}\left(18{\alpha }_1^2+25{\alpha }_2^2+2{\alpha }_3^2+42{\alpha }_1{\alpha }_2-12{\alpha }_1{\alpha }_3-14{\alpha }_2{\alpha }_3\right)-{\alpha }_1-{\alpha }_2-{\alpha }_3\\ \text{ s.t. }& {\alpha }_1+{\alpha }_2-{\alpha }_3=0\\ & {\alpha }_i⩾0,i=1,2,3\end{array}$$

解这一最优化问题. 将 ${\alpha }_3={\alpha }_1+{\alpha }_2$ 代入目标函数并记为
$$s\left({\alpha }_1,{\alpha }_2\right)=4{\alpha }_1^2+\frac{13}{2}{\alpha }_2^2+10{\alpha }_1{\alpha }_2-2{\alpha }_1-2{\alpha }_2$$

对 ${\alpha }_1,{\alpha }_2$ 求偏导数并令其为 0 , 易知 $s\left({\alpha }_1,{\alpha }_2\right)$ 在点 ${\left(\frac{3}{2},-1\right)}^{\mathrm{T}}$ 取极值, 但该点不满足约束条件 ${\alpha }_2⩾0$, 所以最小值应在边界上达到.
当 ${\alpha }_1=0$ 时, 最小值 $s\left(0,\frac{2}{13}\right)=-\frac{2}{13}$; 当 ${\alpha }_2=0$ 时, 最小值 $s\left(\frac{1}{4},0\right)=-\frac{1}{4}$. 于是 $s\left({\alpha }_1,{\alpha }_2\right)$ 在 ${\alpha }_1=\frac{1}{4},{\alpha }_2=0$ 达到最小, 此时 ${\alpha }_3={\alpha }_1+{\alpha }_2=\frac{1}{4}$.

这样, ${\alpha }_1^{\ast }={\alpha }_3^{\ast }=\frac{1}{4}$ 对应的实例点 $x_1,x_3$ 是支持向量. 计算得
$$\begin{array}{c}{w}_1^{\ast }=w_2^{\ast }=\frac{1}{2}\\ b^{\ast }=-2\end{array}$$

分离超平面为
$$\frac{1}{2}{x}^{(1)}+\frac{1}{2}{x}^{(2)}-2=0$$

分类决策函数为
$$f(x)=\mathrm{sign}\left(\frac{1}{2}{x}^{(1)}+\frac{1}{2}{x}^{(2)}-2\right)$$