第二章例2.1软件实现(spss,sas,stata,r)
例2-1`
例2-1 某医院用随机抽样方法检查了138名正常成年女子的红细胞数 ,其测量结果如下,试编制频数分布表。
3.96 4.23 4.42 3.59 5.12 4.02 4.32 3.72 4.76 4.16 4.61 4.26
3.77 4.20 4.36 3.07 4.89 3.97 4.28 3.64 4.66 4.04 4.55 4.25
4.63 3.91 4.41 3.52 5.03 4.01 4.30 4.19 4.75 4.14 4.57 4.26
4.56 3.79 3.89 4.21 4.95 3.98 4.29 3.67 4.69 4.12 4.56 4.26
4.66 4.28 3.83 4.20 5.24 4.02 4.33 3.76 4.81 4.17 3.96 3.27
4.61 4.26 3.96 4.23 3.76 4.01 4.29 3.67 3.39 4.12 4.27 3.61
4.98 4.24 3.83 4.20 3.71 4.03 4.34 4.69 3.62 4.18 4.26 4.36
5.28 4.21 4.42 4.36 3.66 4.02 4.31 4.83 3.59 3.97 3.96 4.49
5.11 4.20 4.36 4.54 3.72 3.97 4.28 4.76 3.21 4.04 4.56 4.25
4.92 4.23 4.47 3.60 5.23 4.02 4.32 4.68 4.76 3.69 4.61 4.26
3.89 4.21 4.36 3.42 5.01 4.01 4.29 3.68 4.71 4.13 4.57 4.26
4.03 5.46 4.16 3.64 4.16 3.76
- 求极差 极差(range)也称全距,即最大值和最小值之差,记作 。本例 。
2.确定组段数和组距 组段数通常取10~15组,分组过多计算繁琐,分组过少难以显现分布特征。组距可通过极差除以组段数求得,一般取方便阅读和计算的数字。本例组距 。
3.根据组距写出组段 每个组段的下限为 、上限为 ,变量 值的归组统一定为 ,最后组段写出上限。起始组段和最后组段应分别包含全部变量值的最小值和最大值,见表2-1第(1)栏。
4.分组划记并统计频数 各组段的频数见表2-1第(2)栏,然后求频数合计,完成频数表。
SPSS代码及结果
大概步骤:分析–描述统计–频率(依次点击即可)
FREQUENCIES
VARIABLES=红细胞数 /FORMAT=NOTABLE # 分析变量
/NTILES= 4 # 四分位数
/PERCENTILES= 2.5 97.5 # 百分位数
/STATISTICS=STDDEV SEMEAN MEAN SKEWNESS SESKEW KURTOSIS SEKURT # 统计量
/HISTOGRAM NORMAL # 直方图
/ORDER= ANALYSIS
SAS代码说明及结果
options nodate;
/*制作频数表*/
data ex2_1;
input x @@;
low=3.07;
dis=0.2;
z=x-mod(x-low,dis);
cards;
3.96 4.23 4.42 3.59 5.12 4.02 4.32 3.72 4.76 4.16 4.61 4.26
3.77 4.20 4.36 3.07 4.89 3.97 4.28 3.64 4.66 4.04 4.55 4.25
4.63 3.91 4.41 3.52 5.03 4.01 4.30 4.19 4.75 4.14 4.57 4.26
4.56 3.79 3.89 4.21 4.95 3.98 4.29 3.67 4.69 4.12 4.56 4.26
4.66 4.28 3.83 4.20 5.24 4.02 4.33 3.76 4.81 4.17 3.96 3.27
4.61 4.26 3.96 4.23 3.76 4.01 4.29 3.67 3.39 4.12 4.27 3.61
4.98 4.24 3.83 4.20 3.71 4.03 4.34 4.69 3.62 4.18 4.26 4.36
5.28 4.21 4.42 4.36 3.66 4.02 4.31 4.83 3.59 3.97 3.96 4.49
5.11 4.20 4.36 4.54 3.72 3.97 4.28 4.76 3.21 4.04 4.56 4.25
4.92 4.23 4.47 3.60 5.23 4.02 4.32 4.68 4.76 3.69 4.61 4.26
3.89 4.21 4.36 3.42 5.01 4.01 4.29 3.68 4.71 4.13 4.57 4.26
4.03 5.46 4.16 3.64 4.16 3.76
;
proc freq;
tables z;
run;
程序说明:创建数据集,用变量low定义最下限,用变量dis定义组距,用mod(x,y)函数新建变量Z,该变量就是将原始变量转换成该数据所在组段的下限值z=x-mod(x-low,dis)
mod(x,y)为取余函数
注意:两个小数求余取值规律:
被除数-(整商×除数)之后在第一位小数位进行四舍五入。 [1]
例:mod(9,1.2)=0.6即:9除以1.2其整商为7;7与除数1.2之积为8.4;被除数9与8.4之差为0.6。故结果为0.6。
用FREQ过程计算下限值的频数,则得到各个组段的频数。
备注:z=x-mod(x-low,dis),各位读者有更好的理解可评论
运行结果

/*用MEANS过程计算例数、均数、标准差、标准误和95%可信区间*/
proc means data=ex2_1
n mean std stderr clm;
var x;
run;
程序说明:调用means过程,计算例数、均数、标准差、标准误和95%可信区间
运行结果

/*用MEANS过程对频数表计算例数、均数、标准差、最小值和最大值*/
data ex2_1_1;
input x f @@;
cards;
3.17 2
3.37 3
3.57 9
3.77 14
3.97 22
4.17 30
4.37 21
4.57 15
4.77 10
4.97 6
5.17 4
5.37 2
;
proc means;
freq f;
var x;
run;
程序说明:在创建数据集时,应设置两个变量,一个变量表示各个组段的组中值,另一个变量为相应组段的频数,means过程中,ferq语句指明哪个变量为频数变量,本例子用f,用var语句指明哪个变量为组中值变量,本例子为x。
结果

/*用UNIVARIATE过程进行描述性统计*/
proc univariate data=ex2_1_1;
freq f;
var x;
run;
程序说明:univariate过程能够给出的描述性统计量比较多,除了means以外,还能输出符号统计量,正态性检验及自定义的百分位数,而且可以生成若干个描述变量分布的茎叶图等统计图。X为分析变量,f为频数变量。
运行结果:

/*计算2.5%和97.5%分位数*/
proc univariate data=ex2_1_1;
var x;
output out=pct
pctlpre=p
pctlpts=2.5 97.5;
run;
proc print data=pct;
run;
程序说明:output语句将univariate产生的部分统计量输出到新建的数据集中,out=pct 就是将要新建的数据集名称为pct,pltpts表示需要计算的百分位数,pctlpre表示新数据集中的变量中的百分位数的前缀,本例子表示为p.
运行结果:

/*作正态性检验、茎叶图、箱式图和正态概率图*/
proc univariate data=ex2_1_1
Normal
plot;
var x;
run;
程序说明:只需在univariate后面加上normal plot选项,就可以输出该组数据正态性检验的结果和茎叶图、箱式图及正态概率图。
运行结果:
STATA代码说明
summarize x /*一般描述、均数、标准差、最小值和最大值*/
summarize x,detail /*详细描述*/
means x /*计算几何均数*/
centile x /*计算中位数*/
centile x,centile(2.5 50 97.5) /*计算百分位数*/
gen group=int((x-3.07)/0.2+0.01)*0.2+3.07 /*产生分组变量*/
tab group /*制作频数表*/
histogram x,frequency bin(12) xlab(3.07(0.2)5.47)norm /*直方图,bin指的是条形数量*/
stem x,round(0.01) /*茎叶图*/
30* | 7
31* |
32* | 17
33* | 9
34* | 2
35* | 299
36* | 0124467789
37* | 12266679
38* | 3399
39* | 166667778
40* | 11122223344
41* | 2234666789
42* | 000011133345566666667888999
43* | 01223466666
44* | 12279
45* | 4566677
46* | 111366899
47* | 15666
48* | 139
49* | 258
50* | 13
51* | 12
52* | 348
53* |
54* | 6
R代码说明及结果
代码
# install.packages("readxl") # 第一运行该文件时加载readxl包用于读取Excel输入数据,将本行开始的#号删除即可
library( readxl ) # 调用外部数据程序包readxl
# 读取Data文件夹下的02_01例题的Excel数据文件(“../Data/E02_01.xls”代表上一级文件夹Data中的E02_01.xls)
E02_01 <- read_excel( "../Data/E02_01.xls" ) # 符号“../” 表示回溯到上一级文件夹
#################### 描述读取的例题数据 ###########################
library(pastecs) # 调用数据程序包pastecs
MyData <-E02_01[[1]]
typeof(MyData)
## [1] "double"
summary(MyData) # 通过summary()计算描述性统计量
#################### 下面为例题的统计分析 ##########################
stat.desc(E02_01$x, norm=TRUE) #通过pastecs包中的stat.desc()函数计算描述性统计量
length(E02_01$x) # 显示对象中元素的数量
max(E02_01$x) # 计算最大值
min(E02_01$x) # 计算最小值
mean(E02_01$x) # 计算平均值
median(E02_01$x) # 计算中位数
sd(E02_01$x) # 计算标准差
var(E02_01$x) # 计算方差
sd(E02_01$x)/sqrt(length(E02_01$x)) # 计算标准误
range(E02_01$x) # 计算值域
quantile(E02_01$x,c(0.025, 0.25, 0.5, 0.75, 0.975)) # 求分位数, 2.5%, 25%, 50%, 75%, 97.5 %的分位点
shapiro.test(E02_01$x) # 夏皮洛-威尔克正态性检验
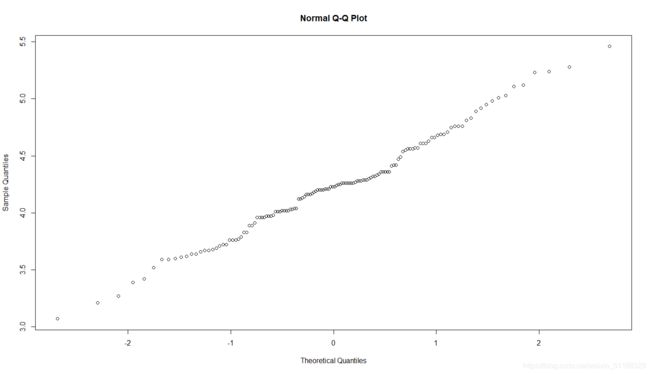
qqnorm( E02_01$x ) # 画出E02_01的Q-Q图
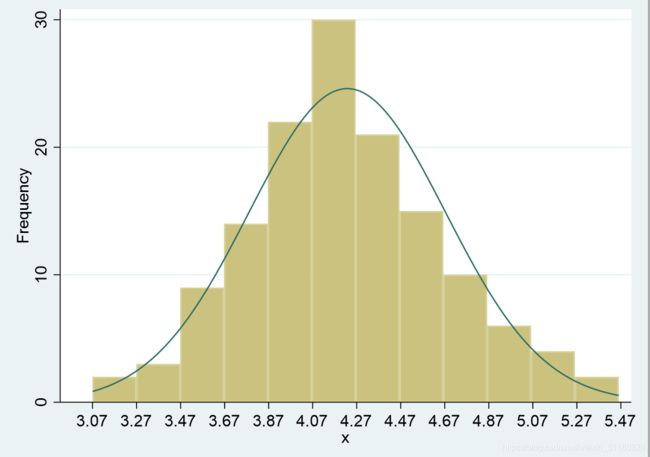
hist(E02_01$x) # 直方图
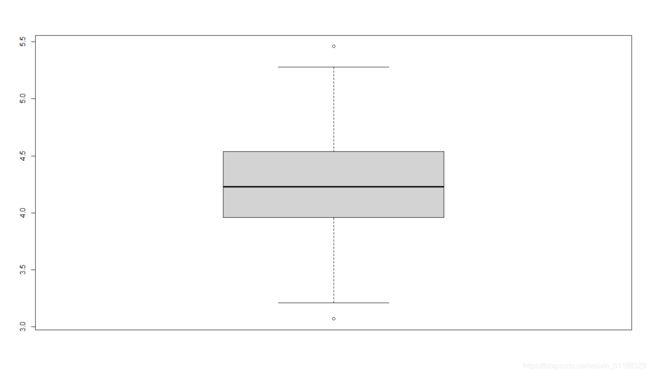
boxplot(E02_01$x) # 箱式图
plot(E02_01$x) # 散点图
stem(E02_01$x) # 将数据序列x从x轴到数据值按照茎状形式画出,以圆圈终止。杆图
X <- pretty( c(2.5, 6), 300 ) # pretty()函数用于创建美观的分割点
# dnorm()函数返回正态分布概率密度函数,求出X点的概率值
TranData <- dnorm( X, mean=mean(E02_01$x), sd = sd(E02_01$x) )
# X与X点的概率值之间的散点图
plot( X, TranData)
```{r E02_01 frequency analysis, message=FALSE, warning=FALSE }
#################### 读取例题02_01的数据 ###########################
library(readxl)
## 读取Data文件夹下的02_01例题的Excel数据文件(“../Data/E02_01.xls”代表上一级文件夹Data中的E02_01.xls)
E02_01 <- read_excel( "../Data/E02_01.xls" ) # 符号“../” 表示回溯到上一级文件夹
MyData <- E02_01[[1]]
#################### 下面为例题的统计分析 ###########################
CurrentRange <- range( MyData ) # 值域
Breaks <- seq( min(MyData),5.5,0.2) # seq()函数用于生成一个序列
Breaks
# cut()函数将连续型变量x分割为有n个水平的因子
MyTable <- cut(MyData, breaks = Breaks,right = TRUE )
MyTable
# 转换为数据框
df <- as.data.frame(table(MyTable))
df
X <- Breaks[1:12]+0.1
X
FinalFreqTable <- data.frame( df, X, fX = df[,2]*X, FX2= df[,2]*X^2 )
FinalFreqTable
运行结果:
#################### 描述读取的例题数据 ###########################
> library(readxl)
> E02_01 <- read_excel("F:/Data/E02_01.xls")
> library(pastecs) # 调用数据程序包pastecs
> MyData <-E02_01[[1]]
> typeof(MyData)
[1] "double"
> ## [1] "double"
> summary(MyData) # 通过summary()计算描述性统计量
Min. 1st Qu. Median Mean 3rd Qu. Max.
3.070 3.962 4.230 4.227 4.527 5.460
>
>
> #################### 下面为例题的统计分析 ##########################
>
> stat.desc(E02_01$x, norm=TRUE) #通过pastecs包中的stat.desc()函数计算描述性统计量
nbr.val nbr.null nbr.na min max range
138.00000000 0.00000000 0.00000000 3.07000000 5.46000000 2.39000000
sum median mean SE.mean CI.mean.0.95 var
583.33000000 4.23000000 4.22702899 0.03794304 0.07502975 0.19867505
std.dev coef.var skewness skew.2SE kurtosis kurt.2SE
0.44572980 0.10544754 0.18690931 0.45301429 0.04348952 0.05306434
normtest.W normtest.p
0.98908446 0.35243661
> length(E02_01$x) # 显示对象中元素的数量
[1] 138
> max(E02_01$x) # 计算最大值
[1] 5.46
> min(E02_01$x) # 计算最小值
[1] 3.07
> mean(E02_01$x) # 计算平均值
[1] 4.227029
> median(E02_01$x) # 计算中位数
[1] 4.23
> sd(E02_01$x) # 计算标准差
[1] 0.4457298
> var(E02_01$x) # 计算方差
[1] 0.1986751
> sd(E02_01$x)/sqrt(length(E02_01$x)) # 计算标准误
[1] 0.03794304
> range(E02_01$x) # 计算值域
[1] 3.07 5.46
> quantile(E02_01$x,c(0.025, 0.25, 0.5, 0.75, 0.975)) # 求分位数, 2.5%, 25%, 50%, 75%, 97.5 %的分位点
2.5% 25% 50% 75% 97.5%
3.40275 3.96250 4.23000 4.52750 5.18325
>
>
> shapiro.test(E02_01$x) # 夏皮洛-威尔克正态性检验
Shapiro-Wilk normality test
data: E02_01$x
W = 0.98908, p-value = 0.3524
> qqnorm( E02_01$x ) # 画出E02_01的Q-Q图
> hist(E02_01$x) # 直方图
> boxplot(E02_01$x) # 箱式图
> plot(E02_01$x) # 散点图
> stem(E02_01$x) # 将数据序列x从x轴到数据值按照茎状形式画出,以圆圈终止。杆图
The decimal point is 1 digit(s) to the left of the |
30 | 7
31 |
32 | 17
33 | 9
34 | 2
35 | 299
36 | 0124467789
37 | 12266679
38 | 3399
39 | 166667778
40 | 11122223344
41 | 2234666789
42 | 000011133345566666667888999
43 | 01223466666
44 | 12279
45 | 4566677
46 | 111366899
47 | 15666
48 | 139
49 | 258
50 | 13
51 | 12
52 | 348
53 |
54 | 6
> X <- pretty( c(2.5, 6), 300 ) # pretty()函数用于创建美观的分割点
> # dnorm()函数返回正态分布概率密度函数,求出X点的概率值
> TranData <- dnorm( X, mean=mean(E02_01$x), sd = sd(E02_01$x) )
> # X与X点的概率值之间的散点图
> plot( X, TranData)
> #################### 下面为例题的统计分析 ###########################
> CurrentRange <- range( MyData ) # 值域
> Breaks <- seq( min(MyData),5.5,0.2) # seq()函数用于生成一个序列
> Breaks
[1] 3.07 3.27 3.47 3.67 3.87 4.07 4.27 4.47 4.67 4.87 5.07 5.27 5.47
> # cut()函数将连续型变量x分割为有n个水平的因子
> MyTable <- cut(MyData, breaks = Breaks,right = TRUE )
> MyTable
[1] (3.87,4.07] (4.07,4.27] (4.27,4.47] (3.47,3.67] (5.07,5.27] (3.87,4.07]
[7] (4.27,4.47] (3.67,3.87] (4.67,4.87] (4.07,4.27] (4.47,4.67] (4.07,4.27]
[13] (3.67,3.87] (4.07,4.27] (4.27,4.47] <NA> (4.87,5.07] (3.87,4.07]
[19] (4.27,4.47] (3.47,3.67] (4.47,4.67] (3.87,4.07] (4.47,4.67] (4.07,4.27]
[25] (4.47,4.67] (3.87,4.07] (4.27,4.47] (3.47,3.67] (4.87,5.07] (3.87,4.07]
[31] (4.27,4.47] (4.07,4.27] (4.67,4.87] (4.07,4.27] (4.47,4.67] (4.07,4.27]
[37] (4.47,4.67] (3.67,3.87] (3.87,4.07] (4.07,4.27] (4.87,5.07] (3.87,4.07]
[43] (4.27,4.47] (3.47,3.67] (4.67,4.87] (4.07,4.27] (4.47,4.67] (4.07,4.27]
[49] (4.47,4.67] (4.27,4.47] (3.67,3.87] (4.07,4.27] (5.07,5.27] (3.87,4.07]
[55] (4.27,4.47] (3.67,3.87] (4.67,4.87] (4.07,4.27] (3.87,4.07] (3.07,3.27]
[61] (4.47,4.67] (4.07,4.27] (3.87,4.07] (4.07,4.27] (3.67,3.87] (3.87,4.07]
[67] (4.27,4.47] (3.47,3.67] (3.27,3.47] (4.07,4.27] (4.07,4.27] (3.47,3.67]
[73] (4.87,5.07] (4.07,4.27] (3.67,3.87] (4.07,4.27] (3.67,3.87] (3.87,4.07]
[79] (4.27,4.47] (4.67,4.87] (3.47,3.67] (4.07,4.27] (4.07,4.27] (4.27,4.47]
[85] (5.27,5.47] (4.07,4.27] (4.27,4.47] (4.27,4.47] (3.47,3.67] (3.87,4.07]
[91] (4.27,4.47] (4.67,4.87] (3.47,3.67] (3.87,4.07] (3.87,4.07] (4.47,4.67]
[97] (5.07,5.27] (4.07,4.27] (4.27,4.47] (4.47,4.67] (3.67,3.87] (3.87,4.07]
[103] (4.27,4.47] (4.67,4.87] (3.07,3.27] (3.87,4.07] (4.47,4.67] (4.07,4.27]
[109] (4.87,5.07] (4.07,4.27] (4.27,4.47] (3.47,3.67] (5.07,5.27] (3.87,4.07]
[115] (4.27,4.47] (4.67,4.87] (4.67,4.87] (3.67,3.87] (4.47,4.67] (4.07,4.27]
[121] (3.87,4.07] (4.07,4.27] (4.27,4.47] (3.27,3.47] (4.87,5.07] (3.87,4.07]
[127] (4.27,4.47] (3.67,3.87] (4.67,4.87] (4.07,4.27] (4.47,4.67] (4.07,4.27]
[133] (3.87,4.07] (5.27,5.47] (4.07,4.27] (3.47,3.67] (4.07,4.27] (3.67,3.87]
12 Levels: (3.07,3.27] (3.27,3.47] (3.47,3.67] (3.67,3.87] ... (5.27,5.47]
>
> # 转换为数据框
> df <- as.data.frame(table(MyTable))
> df
MyTable Freq
1 (3.07,3.27] 2
2 (3.27,3.47] 2
3 (3.47,3.67] 11
4 (3.67,3.87] 12
5 (3.87,4.07] 22
6 (4.07,4.27] 31
7 (4.27,4.47] 21
8 (4.47,4.67] 14
9 (4.67,4.87] 10
10 (4.87,5.07] 6
11 (5.07,5.27] 4
12 (5.27,5.47] 2
>
> X <- Breaks[1:12]+0.1
> X
[1] 3.17 3.37 3.57 3.77 3.97 4.17 4.37 4.57 4.77 4.97 5.17 5.37
> FinalFreqTable <- data.frame( df, X, fX = df[,2]*X, FX2= df[,2]*X^2 )
> FinalFreqTable
MyTable Freq X fX FX2
1 (3.07,3.27] 2 3.17 6.34 20.0978
2 (3.27,3.47] 2 3.37 6.74 22.7138
3 (3.47,3.67] 11 3.57 39.27 140.1939
4 (3.67,3.87] 12 3.77 45.24 170.5548
5 (3.87,4.07] 22 3.97 87.34 346.7398
6 (4.07,4.27] 31 4.17 129.27 539.0559
7 (4.27,4.47] 21 4.37 91.77 401.0349
8 (4.47,4.67] 14 4.57 63.98 292.3886
9 (4.67,4.87] 10 4.77 47.70 227.5290
10 (4.87,5.07] 6 4.97 29.82 148.2054
11 (5.07,5.27] 4 5.17 20.68 106.9156
12 (5.27,5.47] 2 5.37 10.74 57.6738