掌握激活函数（一）：深度学习的成功之源

引言

深度学习作为人工智能领域的一颗璀璨之星，其背后的神经网络模型是无数智能应用的基石。而在这些神经网络中，激活函数担任了不可或缺的角色。它们如同魔法一般，为神经网络带来了非线性特性，使其能够学习和模拟复杂的现实世界模式。没有激活函数，深度学习模型充其量只是一堆线性回归的堆叠。本文将带您逐渐深入掌握激活函数的原理、类型以及在深度学习中的应用，让您真正领略这背后的“魔法”之源。

---

基本概念

激活函数，也称为非线性激活函数，是神经网络中每一层的输出函数。在神经网络的构建中，激活函数发挥着至关重要的作用。它不仅赋予了神经元非线性特性，使得神经网络能够学习和模拟复杂的、非线性的数据模式，更是神经网络表达能力的核心驱动力。没有激活函数，神经网络将仅能执行线性的计算，极大地限制了其应用范围和表达能力。

---

常用激活函数举例

Sigmoid激活函数

Sigmoid函数是一种非常常用的激活函数，它可以将任何输入值映射到0到1之间。这个特性使得Sigmoid函数在二分类问题中特别受欢迎，因为输出可以被解释为属于某一类的概率。

公式

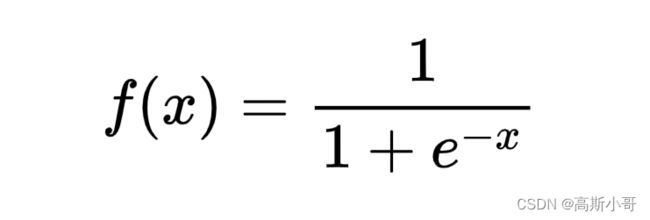
Sigmoid函数的数学特性

特性	描述
非线性	Sigmoid函数可以将输入映射到0-1之间的任意值，允许神经网络学习和模拟复杂的非线性模式。
饱和性	当输入值远离0时，Sigmoid函数的输出会非常接近0或1，这种现象称为饱和。
可微分性	Sigmoid函数是连续且可微的，这意味着基于梯度的优化算法（如反向传播）能够有效地用于训练神经网络。

示例

基于NumPy和PyTorch实现Sigmoid函数

# 基于NumPy实现Sigmoid函数
import numpy as np

def sigmoid(x):
    # 将输入值转换为浮点数
    x = np.float32(x)
    # 计算sigmoid值
    return 1 / (1 + np.exp(-x))

# 基于PyTorch实现Sigmoid函数(使用PyTorch的内置函数torch.sigmoid())
import torch  
  
# 创建一个张量  
x = torch.tensor([-1.0, 0.0, 1.0])  
  
# 应用sigmoid函数  
y = torch.sigmoid(x)  
  
print(y)

# 基于PyTorch实现Sigmoid函数(手动实现)
import torch  

def sigmoid(x):  
    return 1 / (1 + torch.exp(-x))
  
# 创建一个张量  
x = torch.tensor([-1.0, 0.0, 1.0])

# 应用sigmoid函数  
y = sigmoid(x)  

将Sigmoid函数应用于二分类任务

import torch  
import torch.nn as nn  
import torchvision.transforms as transforms  
import torchvision.datasets as datasets  
  
# 定义超参数  
input_size = 784       # 输入图像的维度（28*28）  
hidden_size = 100       # 隐藏层的大小  
num_epochs = 10           # 训练周期数  
batch_size = 100           # 批处理大小  
learning_rate = 0.001       # 学习率  
  
# 加载数据集并进行预处理  
transform = ... # 待定
train_dataset = ... # 待定
test_dataset = ... # 待定
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)  
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=batch_size, shuffle=False)  
  
# 定义模型结构  
class NeuralNetwork(nn.Module):  
    def __init__(self, input_size, hidden_size):  
        super(NeuralNetwork, self).__init__()  
        self.fc1 = nn.Linear(input_size, hidden_size)   
        self.relu = nn.ReLU()  
        self.fc2 = nn.Linear(hidden_size, 1)    
        self.sigmoid = nn.Sigmoid()  # 添加Sigmoid激活函数  
      
    def forward(self, x):  
        out = self.fc1(x)  
        out = self.relu(out)  
        out = self.fc2(out)  
        out = self.sigmoid(out)  # 在输出层使用Sigmoid激活函数  
        return out  
  
# 实例化模型、损失函数和优化器  
model = NeuralNetwork(input_size, hidden_size)  
criterion = ... # 待定
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)  # 使用Adam优化器  
  
# 训练模型  
for epoch in range(num_epochs):  
    for i, (images, labels) in enumerate(train_loader):  # 遍历每个批次的数据  
        # 将图像张量转换为2D张量（矩阵）形式，并作为模型的输入  
        inputs = images.view(-1, input_size)  
        labels = labels.long()  # 将标签转换为长整数型张量  
          
        # 前向传播，计算输出结果  
        outputs = model(inputs)  
        loss = criterion(outputs, labels)  # 计算损失值  
          
        # 反向传播，更新权重参数  
        optimizer.zero_grad()  # 清空梯度缓存，以便计算新的梯度值  
        loss.backward()  # 计算梯度值并累积在模型参数上  
        optimizer.step()  # 更新模型参数  
          

Sigmoid激活函数的局限性举例

Sigmoid函数在深度学习模型中作为激活函数使用，其局限性主要表现在以下几个方面：

1. 梯度消失问题：当输入值非常大或非常小时，Sigmoid函数的导数趋近于0。在深度神经网络中，误差反向传播时，梯度会逐层乘以激活函数的导数。当层数较深时，梯度的连乘可能导致梯度变得非常小，甚至接近于0，使得参数无法有效更新，这就是所谓的梯度消失问题。
2. 输出非0均值：Sigmoid函数的输出值恒大于0，不是0均值的。这会导致后层的神经元的输入是非0均值的信号，对梯度产生影响，进而影响网络的收敛速度(参考链接)。
3. 容易饱和：Sigmoid函数在输入值较大或较小时容易进入饱和区，此时函数的输出对输入的变化不敏感，可能导致模型训练困难。

---

ReLU激活函数

和Sigmoid函数一样，ReLU（Rectified Linear Unit）函数也是非常常用的激活函数。它将负值映射为0，对于正值则直接输出其本身。

公式

ReLU函数的数学特性

特性	描述
简单性	ReLU函数仅需比较输入值和0的大小来确定输出值，计算效率高。
非线性	ReLU函数实际上是非线性的，能够引入非线性因素，增强模型的表达能力。
激活稀疏性	当输入值小于0时，ReLU函数的输出为0，只激活输入中的一部分神经元，增强模型的泛化能力和鲁棒性。
缓解梯度消失问题	与传统的激活函数（如Sigmoid）相比，ReLU有助于缓解梯度消失问题，因为它的梯度在正区间为1，有助于更好地传播梯度。

ReLU函数的特点

1. 线性与非线性：ReLU函数在输入值大于0时表现为线性函数，即f(x)=x，这有助于提高计算速度。而在输入值小于或等于0时，ReLU函数表现为非线性，即输出值为0。这种线性与非线性的结合使得ReLU函数在深度学习中具有很好的性能。

2. 简单高效：ReLU函数的计算过程非常简单，只需要一次比较操作和一次赋值操作，因此计算速度非常快。这使得ReLU函数在训练深度神经网络时非常高效，可以显著加速模型的收敛速度。

3. 缓解梯度消失问题：与Sigmoid等激活函数相比，ReLU激活函数的梯度在反向传播过程中不会消失，有助于提高训练速度和模型的收敛效果。

4. 神经元"死亡"问题：与Sigmoid函数类似，ReLU函数也可能导致某些神经元在训练过程中始终处于"死亡"状态（即输出值一直为0），这可能会影响模型的性能。为了解决这个问题，一些变体的ReLU激活函数也被开发出来，如Leaky ReLU和Parametric ReLU等。

示例

基于NumPy和PyTorch实现ReLU函数

# 基于NumPy实现ReLU函数
import numpy as np  
  
def relu(x):  
    return np.maximum(0, x)
    
# 基于PyTorch实现ReLU函数(使用PyTorch的内置函数F.relu())
import torch.nn.functional as F
  
# 创建一个张量  
x = torch.tensor([-1.0, 0.0, 1.0])  
  
# 应用sigmoid函数  
y = F.relu(x)
  
print(y)

搭建基于ReLU函数的卷积神经网络（CNN）

import torch  
import torch.nn as nn  
  
# 定义一个简单的卷积神经网络  
class SimpleCNN(nn.Module):  
    def __init__(self):  
        super(SimpleCNN, self).__init__()  
        # 第一个卷积层，使用32个3x3的卷积核，输入通道数为1，输出通道数为32，ReLU激活函数  
        self.conv1 = nn.Conv2d(1, 32, 3, padding=1)  
        # 第二个卷积层，使用64个3x3的卷积核，输入通道数为32，输出通道数为64，ReLU激活函数  
        self.conv2 = nn.Conv2d(32, 64, 3, padding=1)  
        # 全连接层，输入节点数为64*7*7（假设输入图像大小为28x28），输出节点数为10（假设有10个类别）  
        self.fc = nn.Linear(64 * 7 * 7, 10)  
        # 输出层，全连接层的输出作为输入，输出节点数为10，使用softmax激活函数  
        self.out = nn.LogSoftmax(dim=1)  
  
    def forward(self, x):  
        # 通过第一个卷积层和ReLU激活函数  
        x = self.conv1(x)  
        x = nn.functional.relu(x)  
        # 通过第二个卷积层和ReLU激活函数  
        x = self.conv2(x)  
        x = nn.functional.relu(x)  
        # 将卷积层的输出展平，作为全连接层的输入  
        x = x.view(x.size(0), -1)  
        # 通过全连接层和softmax激活函数  
        x = self.fc(x)  
        x = self.out(x)  
        return x

在这个示例中：

• 我们定义了一个名为SimpleCNN的类，继承自nn.Module。这是PyTorch中定义神经网络的标准方式。
• 在__init__方法中，我们定义了网络中的各个层。首先有两个卷积层，每个卷积层后都使用了ReLU激活函数。然后是一个全连接层，最后是一个输出层。
• 在forward方法中，我们定义了数据在网络中的前向传播过程。数据首先通过两个卷积层和ReLU激活函数，然后被展平以便输入全连接层，最后通过全连接层和输出层。
• 我们使用了nn.functional模块中的函数来应用ReLU激活函数（nn.functional.relu）和Softmax激活函数（nn.functional.log_softmax）。注意，ReLU激活函数的参数默认为0，因此不需要额外指定。

结束语

• 亲爱的读者，感谢您花时间阅读我们的博客。我们非常重视您的反馈和意见，因此在这里鼓励您对我们的博客进行评论。
• 您的建议和看法对我们来说非常重要，这有助于我们更好地了解您的需求，并提供更高质量的内容和服务。
• 无论您是喜欢我们的博客还是对其有任何疑问或建议，我们都非常期待您的留言。让我们一起互动，共同进步！谢谢您的支持和参与！
• 我会坚持不懈地创作，并持续优化博文质量，为您提供更好的阅读体验。
• 谢谢您的阅读！