算法——字符串
这里结合的是之前一些算法,比如模拟、KMP等,题型比较丰富
最长公共前缀
最长公共前缀
题目解析
- 查找字符串数组中的最长公共前缀。
- 如果不存在公共前缀,返回空字符串 “”
算法原理
解法一:两两比较:定义一个指针i,扫描字符串,当字符串对应位置相同时,移动道下一个位置,直到其中一个字符串到头或者两者对应位置字符不同,结束循环。时间复杂度O(m*n) m为每个字符平均长度,n为字符串个数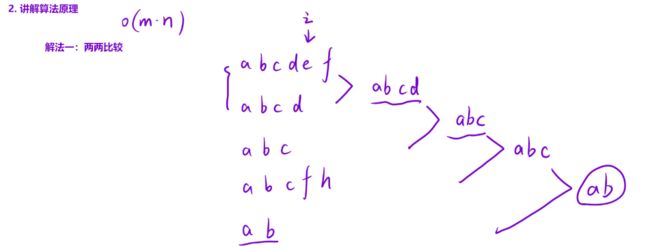
解法二:统一比较
一次比较一竖列,当一竖列都相等时,将他存储到ret里,ret是最终返回的字符串。在比较的时候我们可以那第一个字符串作为标准,例如当比较i位置的时候,拿第一个字符串第i位置的字符作比较,然后拿着该字符和他这一列一一作比较。所以在第一个for循环里,i<第一个字符串的长度即可,当然有些情况需要特判,比如说第一个字符判断到e时,那会发现第二个字符长度不够(这里只是举例子说明,他到不了e就可以停止),即越界,那我们就停止。
j是用来遍历一个一个字符串,从下标1位置开始。是拿j位置的第i个字符和我们刚刚的tmp作比较(tmp是作为基准元素,接下来的j是与第一行第i位置做比较的)如果第j行第i个位置不和tmp位置相等时,说明0~i-1这个位置时最长的公共前缀。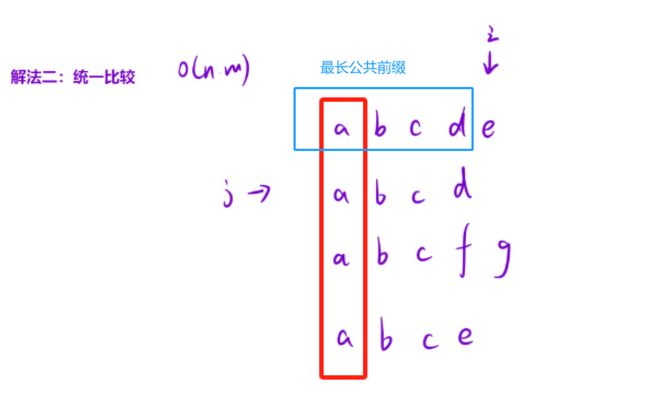
代码实现
class Solution
{
public:
string longestCommonPrefix(vector<string>& strs)
{
// 解法⼀:两两⽐较
string ret = strs[0];
for(int i = 1; i < strs.size(); i++)
ret = findCommon(ret, strs[i]);
return ret;
}
string findCommon(string& s1, string& s2)
{
int i = 0;
while(i < min(s1.size(), s2.size()) && s1[i] == s2[i]) i++;
return s1.substr(0, i);
}
};
class Solution
{
public:
string longestCommonPrefix(vector<string>& strs)
{
// 解法⼆:统⼀⽐较
for(int i = 0; i < strs[0].size(); i++)
{
char tmp = strs[0][i];
for(int j = 1; j < strs.size(); j++)
if(i == strs[j].size() || tmp != strs[j][i])
return strs[0].substr(0, i);
}
return strs[0];
}
};
最长回文子串
最长回文子串
题目解析
- 给你一个字符串 s,找到 s 中最长的回文子串。
- 如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
算法原理
这里我们用中心扩展算法解决:其实本质上还是暴力枚举,只不过我们借助了回文的特性来解决。以i位置为中心,看两边能扩展到什么位置。在中间位置时创建两个指针,分别向两边移动,当两个指针所指的元素相同时,向两边移动,当不相同或者越界时,停止移动,那么两个指针之间的就是最长回文串。但是我们这样枚举出的子串会永远是奇数长度,我们还要考虑偶数长度的情况。所以我们在代码编写的时候,先让left==right,来一次奇数级别的移动,再来一次循环来偶数级别的。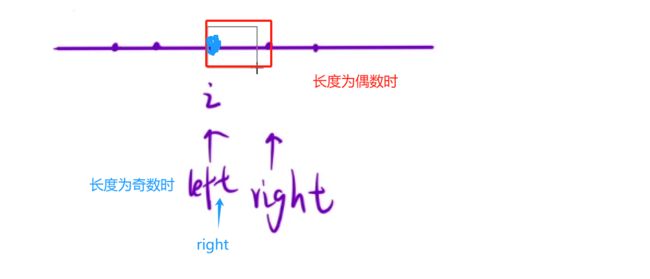

代码实现
class Solution
{
public:
string longestPalindrome(string s)
{
// 中⼼扩展算法
int begin = 0, len = 0, n = s.size();
for(int i = 0; i < n; i++) // 依次枚举所有的中点
{
// 先做⼀次奇数⻓度的扩展
int left = i, right = i;
while(left >= 0 && right < n && s[left] == s[right])
{
left--;
right++;
}
if(right - left - 1 > len) //left和right之间的长度
{
begin = left + 1;
len = right - left - 1;
}
// 偶数⻓度的扩展
left = i, right = i + 1;
while(left >= 0 && right < n && s[left] == s[right])
{
left--;
right++;
}
if(right - left - 1 > len)
{
begin = left + 1;
len = right - left - 1;
}
}
return s.substr(begin, len);
}
};
二进制求和
二进制求和
题目解析
背后是经典的高精度加法(正常数据类型是存不下的,数字非常大),算法思想是模拟。
- 给你两个二进制字符串 a 和 b ,以二进制字符串的形式返回它们的和
算法原理
解法:模拟列竖式运算
用t来模拟两数二进制相加,将其初始化为0,模2进1。从最低位开始加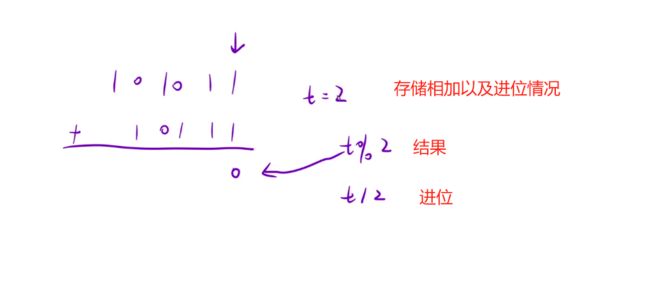
代码实现
class Solution
{
public:
string addBinary(string a, string b)
{
string ret;
int cur1 = a.size() - 1, cur2 = b.size() - 1, t = 0; //因为从最低位开始相加
while(cur1 >= 0 || cur2 >= 0 || t) //是否加完或者看进位上是否还有未加的
{
if(cur1 >= 0) t += a[cur1--] - '0';
if(cur2 >= 0) t += b[cur2--] - '0';
ret += t % 2 + '0';
t /= 2;
}
reverse(ret.begin(), ret.end());
return ret;
}
};
字符串相乘
字符串相乘
题目解析
字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
**注意:**不能使用任何内置的 BigInteger 库或直接将输入转换为整数。 因为这里乘积过后数字很大,就算是double类型也会溢出,所以用字符串形式返回
算法原理
- 解法:模拟小学的列竖式运算
还是用ret存储,然后拿其中一位去乘上面的字符串数字,用tmp记录,然后累加到ret中。即分别将738、615、492分别存储到tmp上,然后再加入ret中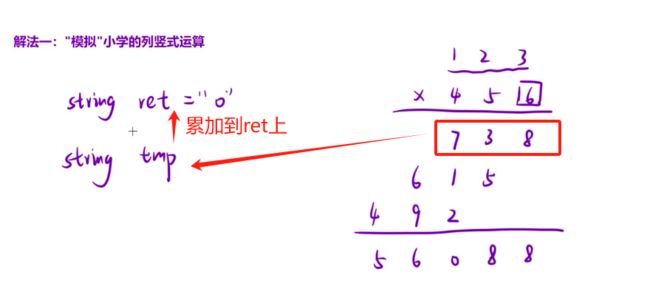
- 细节一:注意高位相乘时,要补上0,这里相加时,是738+6150而不是615.——解决办法:最好是将原字符串逆序。因为我么做运算时,是从最低位开始计算。当我们拿5去和上面数字相乘,此时5的下标位1,正好需要补一个0,同理4的下标位2,补两个0.最终我们放入tmp的结果是逆序的,累加到ret中,最后再逆序一次就得到我们最终求的结果
- 细节二:处理前导0:0去乘1 2 3时分别得到三个0,我们需要把前面两位去掉
- **细节三:注意计算结果的顺序 **返回结果需要再逆序
- 解法二:优化 ——无进位相乘然后相加最后处理进位
创建一个长度为m+n-1的数组,让下面的数去乘上面的数,判断放在哪个位置时,就让两个数字下标相加即可。比如用6去乘3,即都是0位置上,最终18就放在数组0下标的位置上。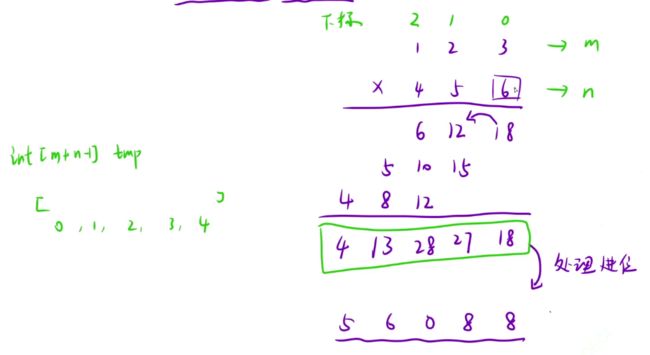
最终处理进位时,就相当于让tmp里的数再和0相加放入ret里就行。最后的最后处理前导0.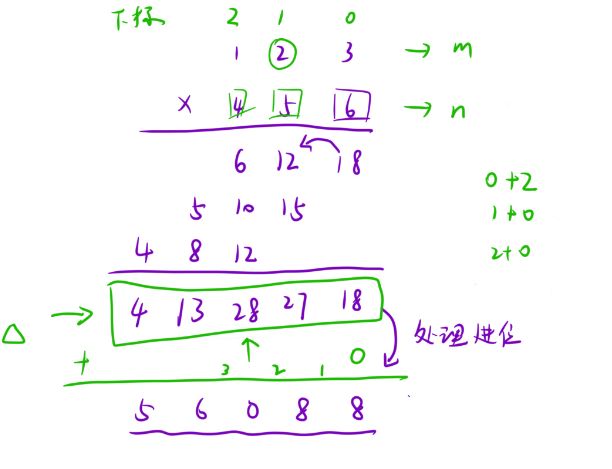
代码实现
class Solution
{
public:
string multiply(string num1, string num2)
{
// 解法:⽆进位相乘后相加,然后处理进位
int m = num1.size(), n = num2.size();
reverse(num1.begin(), num1.end());
reverse(num2.begin(), num2.end());
vector<int> tmp(m + n - 1);
// 1. ⽆进位相乘后相加
for(int i = 0; i < m; i++)
for(int j = 0; j < n; j++)
tmp[i + j] += (num1[i] - '0') * (num2[j] - '0');
// 2. 处理进位
int cur = 0, t = 0;
string ret;
while(cur < m + n - 1 || t)
{
if(cur < m + n - 1) t += tmp[cur++];
ret += t % 10 + '0';
t /= 10;
}
// 3. 处理前导零
while(ret.size() > 1 && ret.back() == '0') ret.pop_back();
reverse(ret.begin(), ret.end());
return ret;
}
};


