C++算法学习四.字符串

 根据代码随想录，记录学习一些算法经验

1.字符串的理论基础

字符串，c++提供一个string类，提供一个size（）接口，判断整个字符串的大小，c只能字符数组使用\0判断字符结束，获得大小。

2.反转字符串（344题）

题目描述：

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。

不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。

你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。

示例 1：
输入：["h","e","l","l","o"]
输出：["o","l","l","e","h"]

使用库函数reverse直接出结果，不建议使用，关键部分用库函数实现，则不使用库函数

class Solution {
public:
    void reverseString(vector& s) {
        for(int i = 0,j = s.size()-1;i < s.size()/2;i++,j--){//双指针，左指针从字符串的左，右指针从字符串的右，中间i

使用了swap库函数，没有使用reverse函数。

字符串也是一种数组，在内存中连续分布。

• 时间复杂度: O(n)
• 空间复杂度: O(1)

3.反转字符串II（541题）

题目描述：

给定一个字符串 s 和一个整数 k，从字符串开头算起, 每计数至 2k 个字符，就反转这 2k 个字符中的前 k 个字符。

如果剩余字符少于 k 个，则将剩余字符全部反转。

如果剩余字符小于 2k 但大于或等于 k 个，则反转前 k 个字符，其余字符保持原样。

示例:

输入: s = "abcdefg", k = 2
输出: "bacdfeg"

库函数解法:使用库函数reverse函数直接操作，在循环上做文章即可

class Solution {
public:
    string reverseStr(string s, int k) {
        for(int i = 0;i < s.size();i+=(2*k)){//前2k个字符的前k个字符进行反转
            if(i+k < s.size()){//反转2k字符的前k个字符
                reverse(s.begin()+i,s.begin()+i+k);//
                continue;
            }
            reverse(s.begin()+i,s.begin()+s.size());//不满足字符个数>k,但是小于2k，反转所有字符
        }
        return s;
    }
};

• 时间复杂度: O(n)
• 空间复杂度: O(1)

 自己实现的reverse函数：

class Solution {
public:
    void reverse(string &s,int strat,int end){
        for(int i = strat,j = end;i < j;i++,j--){
            swap(s[i],s[j]);
        }
    }
    string reverseStr(string s, int k) {
        for(int i = 0;i < s.size();i+=(2*k)){
            if(i + k <= s.size()){
                reverse(s,i,i+k-1);
                continue;
            }
            reverse(s,i,s.size()-1);
        }
        return s;
    }
};

4.替换数字（卡码网）

题目描述：

给定一个字符串 s，它包含小写字母和数字字符，请编写一个函数，将字符串中的字母字符保持不变，而将每个数字字符替换为number。

例如，对于输入字符串 "a1b2c3"，函数应该将其转换为 "anumberbnumbercnumber"。

对于输入字符串 "a5b"，函数应该将其转换为 "anumberb"

额外空间方法：申请一块额外的字符串，

#include
#include
using namespace std;

int main(){
    string s{ };
    string a{ };//申请额外的数组，存储结果
    cin >> s;//输入字符串
    for(char& c : s){//每个字符遍历，遇到数字的ascii值
        if(c>=48 && c<=57){//数字进行替换
            a+="number";
        }else{
            a+=c;//按照原来的输出
        }
    }
    cout<

双指针做法：

数组填充问题，做法都是先预先给数组扩容带填充后的大小，然后在从后向前进行操作。

不用申请新的内存空间，从后向前填充，避免移动数组带来不必要的时消耗，

#include
#include
using namespace std;

int main(){
    string s;
    while(cin>>s){
        int count = 0;//记录元素个数
        int size = s.size();//记录之前数组大小，也是双指针其中一个指针的位置
        for(int i = 0;i < s.size();i++){//记录字符串中有几个数字
            if(s[i]>='0' && s[i]<='9'){
                count++;
            }
        }
        s.resize(5*count+s.size());//对字符串数组扩容
        int newsize = s.size();//记录扩容之后的大小，也就是双指针的其中一个位置
        for(int i = newsize-1 ,j = size-1;j'9'||s[j]<0){//不是数字不改变
                s[i] = s[j];
            }else{//数字改变成number
                s[i] = 'r';
                s[i-1] = 'e';
                s[i - 2] = 'b';
                s[i - 3] = 'm';
                s[i - 4] = 'u';
                s[i - 5] = 'n';
                i -= 5;
            }
        }
        cout<< s <

• 时间复杂度：O(n)
• 空间复杂度：O(1)

 5.翻转字符串里的单词（151题）

题目描述：给定一个字符串，逐个翻转字符串中的每个单词。

示例 1：
输入: "the sky is blue"
输出: "blue is sky the"

思路：移除多余空格，将整个字符串反转，然后再将单词翻转，使用擦除函数就是实现可能实现时间复杂度比较高，其实也就是移除元素和反转字符串的合起来的应用。

class Solution {
public:
    void reverse(string& s, int start, int end) {//定义一个反转函数自己实现的双指针操作
        for (int i = start, j = end; i < j; i++, j--) {//在开始和结束位置，定义两个指针进行操作
            swap(s[i], s[j]);
        }
    }
    void removeExtraSpaces(string& s) {//删除多余空格，使用的是双指针方法，类似删除元素的操作
        int slow = 0;//慢指针
        for (int i = 0; i < s.size(); i++) {//快指针
            if (s[i] != ' ') {//处理多余空格
                if (slow != 0)//首位空格去掉，其他部分单词之间留出空格
                    s[slow++] = ' ';
                while (i < s.size() && s[i] != ' ') {//一个单词操作，两个指针同时移动
                    s[slow++] = s[i++];
                }
            }
        }
        s.resize(slow);//重新定义字符串的大小
    }
    string reverseWords(string s) {
        removeExtraSpaces(s);//删除多余空格
        reverse(s, 0, s.size() - 1);//反转全部字符串
        int start = 0;//慢指针
        for (int i = 0; i <= s.size(); ++i) {//快指针
            if (i == s.size() || s[i] == ' ') {//找到一个单词
                reverse(s, start, i - 1);//进行反转
                start = i + 1;//更新下标
            }
        }
        return s;
    }
};

• 时间复杂度: O(n)
• 空间复杂度: O(1) 或 O(n)

6.右旋转字符串（卡码网）

题目描述：

字符串的右旋转操作是把字符串尾部的若干个字符转移到字符串的前面。给定一个字符串 s 和一个正整数 k，请编写一个函数，将字符串中的后面 k 个字符移到字符串的前面，实现字符串的右旋转操作。

例如，对于输入字符串 "abcdefg" 和整数 2，函数应该将其转换为 "fgabcde"。

思路：就是将字符串先整个反转，然后再将左部分翻转，再将右部分翻转即可。

#include
#include
using namespace std;

void reverse(string& s, int start, int end){//自己实现的翻转函数
    for(int i = start, j = end; i < j; i++, j--){
        swap(s[i],s[j]);
    }
}
int main(){
    string s;
    int k;//输入的翻转位置
    cin>>k;
    while(cin>>s输入字符串
        reverse(s,0,s.size());//反转整个字符串
        reverse(s,0,k);//做了左部分的翻转
        reverse(s,k,s.size());//右部分的翻转
    }
    cout<

其实实现思路比较简单想明白就可以实现功能。

7.kmp算法的理论基础

kmp算法思想：当出现字符串不匹配时，可以记录一部分之前已经匹配的文本内容，利用这些信息避免从头再去做匹配。

KMP主要应用在字符串匹配上。next数组，

前缀表：next数组就是一个前缀表，前缀表是用来回退的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。

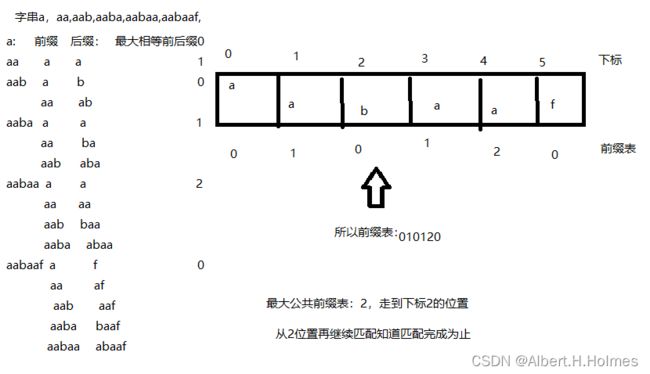
例：要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf。

前缀表就是避免重复的查找，如果匹配失败，定位匹配上的位置，重新开始匹配，也就是告知之后应该从哪个位置开始重新匹配。

前缀表：记录下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。

前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。

后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。

前缀表要求的就是相同前后缀的长度。下面是计算前缀表的过程。

 下标5之前这部分的字符串（也就是字符串aabaa）的最长相等的前缀 和 后缀字符串是 子字符串aa ，因为找到了最长相等的前缀和后缀，匹配失败的位置是后缀子串的后面，那么我们找到与其相同的前缀的后面重新匹配就可以了。

我们需要从找不到的位置看之前前缀表， next数组就可以是前缀表，但是很多实现都是把前缀表统一减一（右移一位，初始位置为-1）之后作为next数组。

n为文本串长度，m为模式串长度，整个KMP算法的时间复杂度是O(n+m)的。

8.找出字符串中第一个匹配项的下标（28题）

题目描述：给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回  -1 。

使用kmp算法来求解：首先构建一个next数组，初始化next数组，处理前后缀不相同情况，处理前后缀相同情况，定义两个指针i,j，j指向前缀起始的位置，i指向后缀起始的位置。

例如前缀表不减一的操作，设置int j = 0;next[j] = 0前后缀不相同情况：回退前一个前缀表位置j=next[j-1]；前后缀相同情况：j++;next[i]=j;

class Solution {
public:
    void getnext(int* next,const string& s){//构建前缀表数组函数
        int j = 0;//定义j指针并对其初始化
        next[j] = 0;//数组也要初始化，其实是第一个字符子串的最长相同前后缀长度
        for(int i = 1;i < s.size();i++){//快指针遍历整个数组下标，注意i从1开始
            while(j > 0 && s[i] != s[j]){//处理前后缀不相同情况，j要回退
                j = next[j-1];
            }
            if(s[i] == s[j]){//处理前后缀相同情况，将j的长度赋给next[i]
                j++;
            }
            next[i] = j;
        }
    }
    int strStr(string haystack, string needle) {//实现函数
        if(needle.size() == 0){//如果模式串大小等于0直接返回
            return 0;
        }
        int next[needle.size()];//构建数组，生成前缀表
        getnext(next,needle);
        int j = 0;//定义j指针
        for(int i = 0; i < haystack.size(); i++){//注意i从0开始
            while(j > 0 && haystack[i] != needle[j]){//不匹配
                j = next[j-1];//回退之前匹配位置
            }
            if(haystack[i] == needle[j]){//匹配，同时向前移动
                j++;
            }
            if(j == needle.size()){//文本串出现了模式串返回下标
                return (i - needle.size()+1);
            }
        }
        return -1;
    }
};

注：构建前缀表的数组i从1开始的，数组的j初始化0，next[j]初始化0，其他注意即可。

下面是前缀表减一的操作：

class Solution {
public:
    void getnext(int* next,const string& s){//构建前缀表数组函数
        int j = -1;//定义j指针并对其初始化
        next[0] = j;//数组也要初始化，其实是第一个字符子串的最长相同前后缀长度
        for(int i = 1;i < s.size();i++){//快指针遍历整个数组下标，注意i从1开始
            while(j >= 0 && s[i] != s[j+1]){//处理前后缀不相同情况，j要回退
                j = next[j];
            }
            if(s[i] == s[j+1]){//处理前后缀相同情况，将j的长度赋给next[i]
                j++;
            }
            next[i] = j;
        }
    }
    int strStr(string haystack, string needle) {//实现函数
        if(needle.size() == 0){//如果模式串大小等于0直接返回
            return 0;
        }
        int next[needle.size()];//构建数组，生成前缀表
        getnext(next,needle);
        int j = -1;//定义j指针
        for(int i = 0; i < haystack.size(); i++){//注意i从0开始
            while(j >= 0 && haystack[i] != needle[j+1]){//不匹配
                j = next[j];//回退之前匹配位置
            }
            if(haystack[i] == needle[j+1]){//匹配，同时向前移动
                j++;
            }
            if(j == needle.size()-1){//文本串出现了模式串返回下标
                return (i - needle.size()+1);
            }
        }
        return -1;
    }
};

• 时间复杂度: O(n + m)
• 空间复杂度: O(m)

注：前缀表的构建以及匹配的操作，还有何时跳出。

9.重复的子字符串（459题）

题目描述：

给定一个非空的字符串，判断它是否可以由它的一个子串重复多次构成。给定的字符串只含有小写英文字母，并且长度不超过10000。

示例 1:

• 输入: "abab"
• 输出: True
• 解释: 可由子字符串 "ab" 重复两次构成。

 使用kmp算法来解决：kmp解决一个串是否出现过另一个串，前缀表里，统计了各个位置为终点字符串的最长相同前后缀的长度。最长相等前后缀的长度为：next[len - 1] + 1。如果len % (len - (next[len - 1] + 1)) == 0 ，则说明数组的长度正好可以被 (数组长度-最长相等前后缀的长度) 整除 ，说明该字符串有重复的子字符串。数组长度减去最长相同前后缀的长度相当于是第一个周期的长度，也就是一个周期的长度，如果这个周期可以被整除，就说明整个数组就是这个周期的循环。

class Solution {
public:
    void getnext(int* next, string& s){//构建next前缀表数组
        int j = 0;//初始化，这部分采用原始前缀表
        next[j] = 0;
        for(int i = 1;i < s.size();i++){//注意i从1开始
            while(j > 0 && s[i] != s[j]){//处理前后缀不相同情况
                j = next[j-1];
            }
            if(s[i] == s[j]){//处理前后缀相同情况
                j++;
            }
            next[i] = j;
        }
    }
    bool repeatedSubstringPattern(string s) {//实现函数
        int next[s.size()];//构建数组
        getnext(next,s);
        int len = s.size();//求长度
        if(next[len - 1] != 0 && len % (len - (next[len - 1])) == 0){//满足的条件
            return true;
        }
        return false;
    }
};

• 时间复杂度: O(n)
• 空间复杂度: O(n)

 移动匹配：如果有相同重复子串，两个字符串拼接起来也一定会有字符串出现，那么断定有重复的子串，首先需要抛出第一个和最后一个字符，

class Solution {
public:
    bool repeatedSubstringPattern(string s) {
        string t = s + s;//拼接两个字符串
        t.erase(t.begin());//去掉头字符和尾字符
        t.erase(t.end() - 1);
        if(t.find(s) != std::string::npos){//如果找到相同字符串返回正确
            return true;
        }
        return false;
    }
};

• 时间复杂度: O(n)
• 空间复杂度: O(1)

 总结：

字符串的理论基础：其实是字符串数组，c++提供了size接口可以知道字符串的大小

反转字符串：reverse函数的自我实现，双指针，使用swap函数实现

反转字符串II：翻转一个长度固定的字符串，然后每隔k个字符进行反转，前部分翻转后面k字符不翻转，注意使用for循环步长设定即可，

替换数字：可以申请额外空间进行操作，如果字符是数字则加入固定的字符串，经典数组填充问题，需要从后向前填充，首先先对数组进行扩容，记录新数组大小，定义两个指针，两个指针的起始位置都是从后面开始，后面可以覆盖。

翻转字符串里的单词：首先去掉多余的空格，再全部反转字符，再每一个单词进行反转即可实现，这里使用双指针进行操作就可以实现删除多余空格，自己定义的翻转函数，删除空格部分有点绕，不过想通了，很好的一道题！

右旋转字符串：这个就是自己实现一个反转函数，然后整体字符翻转，再将分割两个部分翻转即可。

kmp算法理论：常用字符串匹配问题，不匹配时，记录匹配的文本，避免从头匹配，前缀表next数组存放最大相等的前后缀长度，要了解前缀和后缀概念，知道如何计算前缀表

找出字符串匹配的下标：首先构建next数组，初始化next数组，然后再处理前后缀不相等的情况，处理前后缀相等情况，前缀表有两种形式-1和正常，前缀表要回退前一个下标的next数组位置，还有注意i从1开始遍历，值得多看几遍这个题很好，思考有点绕，不过想法很好。

重复子字符串：kmp算法查看是否出现相同子串，数组的长度正好可以被 (数组长度-最长相等前后缀的长度) 整除 ，字符串有重复的子字符串，注意条件设定，其他kmp算法老生常谈，移动匹配思想很好，将两个字符串拼接在一起，去掉第一个字符和最后一个字符，如果还有s字符串代表有重复字符串，很好的想法，kmp算法真的好好复习！！！！！！！