力扣:968. 监控二叉树(贪心,二叉树)
题目:
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
输入:[0,0,null,0,0]
输出:1
解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
输入:[0,0,null,0,null,0,null,null,0]
输出:2
解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。
思路:
这道题目首先要想,如何放置,才能让摄像头最小的呢?
从题目中示例,其实可以得到启发,我们发现题目示例中的摄像头都没有放在叶子节点上!
这是很重要的一个线索,摄像头可以覆盖上中下三层,如果把摄像头放在叶子节点上,就浪费的一层的覆盖。
所以把摄像头放在叶子节点的父节点位置,才能充分利用摄像头的覆盖面积。
为什么不从头结点开始看起呢,为啥要从叶子节点看呢?
因为头结点放不放摄像头也就省下一个摄像头, 叶子节点放不放摄像头省下了的摄像头数量是指数阶别的。
所以我们要从下往上看,局部最优:让叶子节点的父节点安摄像头,所用摄像头最少,整体最优:全部摄像头数量所用最少!局部最优推出全局最优
此时,大体思路就是从低到上,先给叶子节点父节点放个摄像头,然后隔两个节点放一个摄像头,直至到二叉树头结点。
此时这道题目还有两个难点:
- 二叉树的遍历
- 如何隔两个节点放一个摄像头
确定遍历顺序
因为是从下往上推,所以采用后序(左右中)遍历顺序
如何隔两个节点放一个摄像头
首先来分析每个节点可能出现的状态
每个节点可能有三种状态:
- 该节点无覆盖
- 本节点有摄像头
- 本节点有覆盖
我们分别有三个数字来表示:
- 0:该节点无覆盖
- 1:本节点有摄像头
- 2:本节点有覆盖
因为在遍历树的过程中,就会遇到空节点,那么问题来了,空节点究竟是哪一种状态呢? 空节点表示无覆盖? 表示有摄像头?还是有覆盖呢?
回归本质,为了让摄像头数量最少,我们要尽量让叶子节点的父节点安装摄像头,这样才能摄像头的数量最少。
那么空节点不能是无覆盖的状态,这样叶子节点就要放摄像头了,空节点也不能是有摄像头的状态,这样叶子节点的父节点就没有必要放摄像头了,而是可以把摄像头放在叶子节点的爷爷节点上。
所以空节点的状态只能是有覆盖,这样就可以在叶子节点的父节点放摄像头了
接下来就是递推关系。
那么递归的终止条件应该是遇到了空节点,此时应该返回2(有覆盖),原因上面已经解释过了。
代码如下:
if not root:
return 2 # 如果节点为空,返回2表示该节点被覆盖
递归的函数,以及终止条件已经确定了,再来看单层逻辑处理。
主要有如下四类情况:
- 情况1:左右节点都有覆盖
左孩子有覆盖,右孩子有覆盖,那么此时中间节点应该就是无覆盖的状态了。
下图采用代码随想录的图:
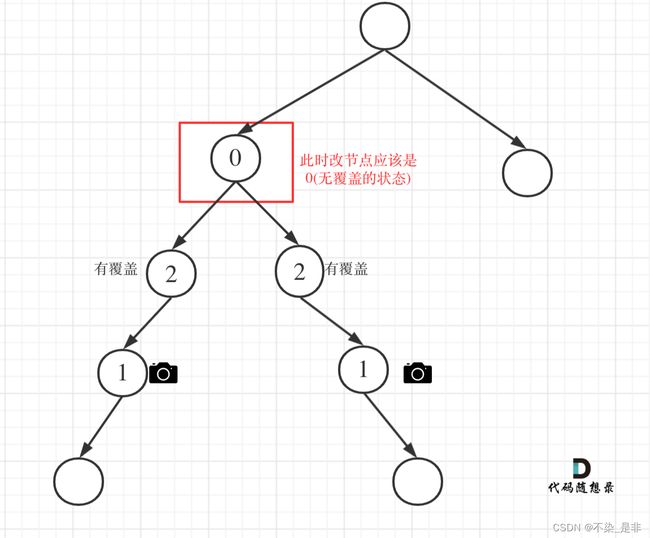
代码如下:
if left == 2 and right == 2:
return 0 # 如果左右子节点都被覆盖,当前节点未被覆盖
- 情况2:左右节点至少有一个无覆盖的情况
只要左右孩子中有一个无覆盖,则父节点都应该安摄像头
代码如下:
if left == 0 or right == 0:
self.result += 1 # 如果左子节点或右子节点未被覆盖,需要在当前节点放置摄像头
return 1 # 返回1表示当前节点放置了摄像头
- 情况3:左右节点至少有一个有摄像头
左右孩子节点有一个有摄像头了,那么其父节点就应该是2(覆盖的状态)
代码如下:
if left == 1 or right == 1:
return 2 # 如果左子节点或右子节点放置了摄像头,当前节点被覆盖
其实还有一种情况,左右孩子都有摄像头,但父节点是根节点,到父节点后就遍历完树了,但根节点未覆盖
- 情况4:头结点没有覆盖
如图:
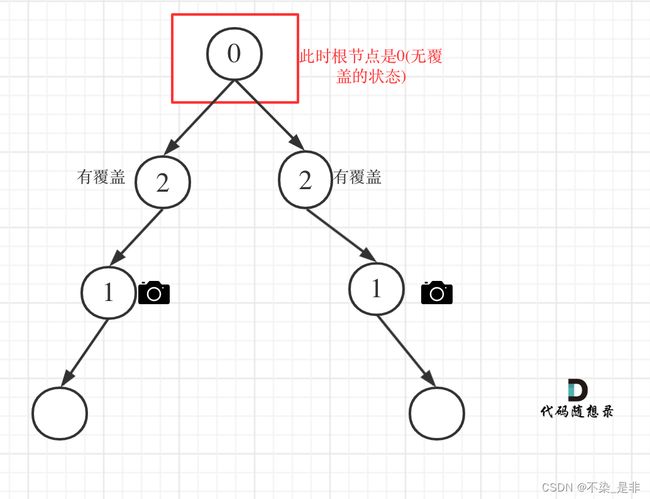
所以递归结束之后,还要判断根节点,如果没有覆盖,self.result += 1,代码如下:
def minCameraCover(self, root: Optional[TreeNode]) -> int:
self.result = 0 # 初始化,用于存储最小摄像头数量
if self.traversal(root) == 0:
self.result += 1
return self.result
以上就是所有分析
完整代码:
# 这是一个二叉树节点的定义
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val # 节点的值
# self.left = left # 左子节点
# self.right = right # 右子节点
# 从下往上安装摄像头:跳过leaves这样安装数量最少,局部最优 -> 全局最优
# 先给leaves的父节点安装,然后每隔两层节点安装一个摄像头,直到Head
# 0: 该节点未覆盖
# 1: 该节点有摄像头
# 2: 该节点有覆盖
class Solution:
def minCameraCover(self, root: Optional[TreeNode]) -> int:
self.result = 0 # 初始化,用于存储最小摄像头数量
if self.traversal(root) == 0:
self.result += 1
return self.result
def traversal(self, root):
if not root:
return 2 # 如果节点为空,返回2表示该节点被覆盖
left = self.traversal(root.left) # 递归遍历左子树
right = self.traversal(root.right) # 递归遍历右子树
if left == 0 or right == 0:
self.result += 1 # 如果左子节点或右子节点未被覆盖,需要在当前节点放置摄像头
return 1 # 返回1表示当前节点放置了摄像头
if left == 1 or right == 1:
return 2 # 如果左子节点或右子节点放置了摄像头,当前节点被覆盖
if left == 2 and right == 2:
return 0 # 如果左右子节点都被覆盖,当前节点未被覆盖
复杂度分析:
- 时间复杂度: O(n),需要遍历二叉树上的每个节点
- 空间复杂度: O(n)