AVL树(超详解)
文章目录
- 前言
- AVL树的概念
- AVL树的实现
-
- 定义AVL树
- insert
- 单旋
-
- 左单旋
- 右单旋
- 左单旋代码
- 右单旋代码
- 双旋
-
- 左右双旋
- 右左双旋
- 测试
- AVL树的性能
前言
AVL树是怎么来的呢?
我们知道搜索二叉树会存在退化问题,退化以后就变成单支或者接近单支。
它的效率就变成O(N)了,无法保证搜索效率。
无法保证搜索效率我们就必须做一件事,
我们得去控制平衡。
AVL树的概念
看到上面的解决方案,我们肯定会思考一个问题,
为什么是左右高度差不超过1,而不是相等呢?
因为做不到,一个结点可以做到相等,两个结点怎么做都做不到,
因为你的值是一个一个插入的,无法保证数据个数。就比如下面的图:

有些结点数量是永远保证不了的
AVL树实现有很多种方式,我们这里使用下面这一种方式来控制平衡。
这种方式叫做平衡因子。
我们引入了平衡因子来控制平衡。
![]()
平衡因子就是左右高度差,右减左。

任何一个结点都有一个平衡因子,只要所有结点平衡因子都是
0,1,-1,它就是AVL树
看一颗树是不是AVL树:
如果它的平衡因子百分之百正确的话,只需要看它的平衡因子。
AVL树的实现
定义AVL树
我们直接定义成key/value结构,因为能实现key/value就能实现key,并且它们本质也差不多

在这里我们第一次引入三叉链,也就是除了_left,_right还有parent,
没有parent也可以,但是实现起来麻烦很多。
parnet也带来了额外的负担,就像单链表改为双向链表以后,我们多了一个指针来维护。
这里有个三叉链,有个parent,就可以向上倒着遍历,但是如果进行调整,插入的时候就要维护这个指针。
以前我们是没有使用parent指针的,但是这会付出很大的代价,我们后面会说,
我们在做旋转的时候这个会非常恶心,但是这个指针又带来了很强的便利性。
这里我们构造就懒得写,直接给个参数
insert
首先插入一个值。
![]()
AVL树插入值没有什么诀窍,跟我们之前文章的搜索树是一样的。
可以用递归可以用非递归,我们这里推荐用非递归,这种写循环就非常
顺畅的我们就没有用递归了。




这里有个问题,父指针是怎么链接的呢?
我们可以再处理一步。来个反向链接。
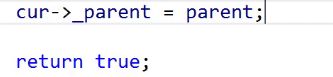
parent是怎么链接上的呢?
根不需要链接,根没有父亲,但其他结点都有父亲。
其他结点比它大往右边走,比它小往左边走,然后插入了以后,
跟父亲的左右链接了,自己要反向过来链接父亲。
搜索树的部分已经完成了,AVL树才刚刚开始。
AVL树插入了怎么办呢?
根据插入的结点位置可以分为下面的一些情况。

新增结点的平衡因子是多少?
首先影响一个结点平衡因子的因素是什么?左右子树的高度。
新增结点的平衡因子不用想,肯定都是0.因为它左树和右树的高度没有任何影响。
怎么衡量一颗树有没有受到影响呢?比如有没有出问题呢,需要我们处理一下。
怎么衡量,更新平衡因子。新增结点是0,就不用说了。

旋转是我们说到的最重要的一个概念。这是个比较复杂的东西,我们后面会讲解。
我们新增一个结点会影响哪些结点?
它只会影响它的祖先,从它到根的路径下的结点。

更准确讲,插入一个结点指挥影响它的部分祖先结点。
到底会影响谁,不好说。
所以我们得沿着路径往上更新。
所以我们也就清楚前面为什么要加parent
不加parent不好处理,加了parent才好处理。
我们现在来分析一下平衡因子如何更新?
如果新增结点在父亲的左边怎么办?如果新增结点在父亲的右边怎么办?
父亲的平衡因子怎么办?
新增结点意味着子树的高度变化。子树的高度变化就会影响父亲的平衡因子。


注意,它不一定所有的祖先会受到影响。
我们继续要往上更新,有三叉链就很好走。
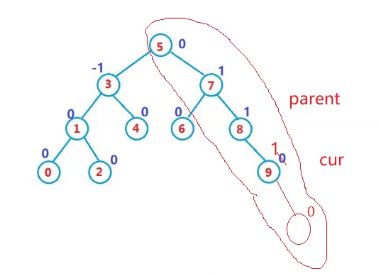
要不要往上更新,取决于更新完一遍以后,父亲的平衡因子怎么办。
这个时候又分为三种情况。
什么决定了要不要往上更新?

旋转怎么办?我们这里先说结论
旋转完,它就好了,它的本质是降低高度,它又恢复之前的高度,
并且它又变成平衡树了。
旋转又有四种旋转,而且还很复杂。
第三种情况:
变成0,要不要继续往上更新?
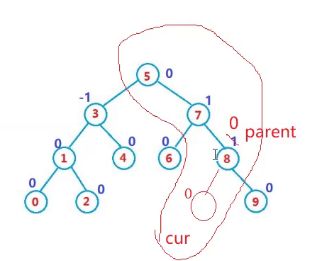

0不需要继续往上更新,0就像相当于把我给治愈了,
由相对平衡变成绝对平衡了。 它不需要继续玩了。
到现在AVL树的大框架已经完成了.
有时候需要不断更新,一直更新到根节点。像下面这种情况。

现在要插入一个结点。

为什么不建议直接用else呢?
有可能这棵树在插入之前就已经出问题了。
比如有些结点的平衡因子插入之前就是2,-2或者更大,都混到这个情况里就很麻烦。
上面也就是AVL树的大框架
当出现局部的不平衡怎么办?这里先说一个简单的情况
这里是最简单的一种情况,叫做单旋。还要延伸出很多种情况,慢慢处理。
但是无论哪种形状都可以通过旋转,让它平衡且降低高度。
旋转有两大目的:
1.把这颗子树从不平衡变成平衡
2.降低这颗子树的高度。
注意AVL树可以直接控制高度,比如插入一个结点去看左树和
右树的高度差有没有问题,出现问题再去处理。
但是这种实时的方式不那么好控制。我们这里是引入了平衡因子。
单旋
接下来我们要把四种旋转讲清楚,而且这四种旋转还挺复杂的,
我们一点一点讲。
左单旋
我们先来看最简单的情况,上面已经提到过。这种情况感觉很简单,
但实际会很复杂的。
插入结点之后,这颗树的右边高,我们就往它的左边进行旋转。
看起来是下面这样,我们来分析一下它的实际是怎么样子 。

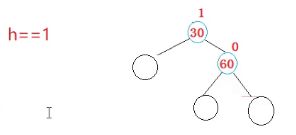
刚才的情况右边高,它叫做左单旋。
旋转的这颗树不一定是整棵树,他可能是局部的一颗子树。

h为2的情况就多了。

我们先说结论,等下再具体解释

我们先随便画一种出来看一下

看,它符合30和60的平衡因子。
当然a,b也可能是y,z;
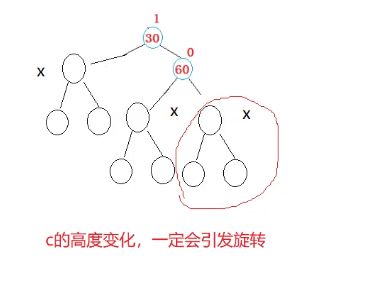
具象图无穷无尽,而且越往下组合情况越多,我们这里只是举例到了h==2;
只要c的高度发生变化就会引发旋转。
c种插入一个结点都会引发30bf变成2;
具体可以自己演示
c为什么只能是y,z?
c是y,z不会影响30bf变成2,为什么?
假设c是y这个样子

如果我是从最下面插入
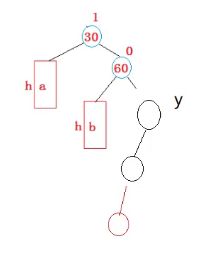
现在这样的话,y自己就出问题了,它自己要旋转,不会到30.
如果这样插入
![]()
由-1变成0,它就不会继续往上更新。
看上面只有变成x,才能任意一个位置插入都会引发旋转
因为如果是y,z的话,要么就是自己会引发旋转,要么就是不会影响旋转,只是让它自己变平衡
我们先把30bf的变成2的情况都分析出来
我们不可能把h的情况画完,那AVL树到底怎么走?
它们是刚才的任意一种情况,它们的处理规则都是一样的。
也就是当c这颗树的高度从0变成1,从1变成2,从2变成3,
它都会引发30bf变成2.
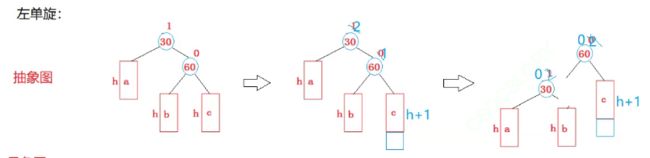
它的旋转简单总结就是两步,看起来简单,但是等下我们处理起来有一些麻烦

为什么这么变呢?

我们怎么保持搜索树的规则呢?
b为什么可以变成30的右边?
b这棵树的结点比30大比60小,所以变成30的右边肯定是没有问题的。
可以看到30这颗树整体都比60小。
旋转不是乱旋,它是保持搜索树的规则。
上面我们讲了旋转的目的,旋转的原则,旋转的过程
面试不会让你手撕一颗AVL树,但是可能会让你讲这个过程,
为什么这么旋转一定要分析得清清楚楚。
我们为什么要这样旋转?
因为旋转有无数多种情况,就像h有数种情况,组合起来也有无数种,
但是不管h有多少种情况,旋转方式都是一样的。
右单旋
在讲这个左单旋的之前,我们可以把左单旋画一下,在哪里插入会引发旋转,
画一两个具象图看一下
左单旋代码
接着我们把代码写上一些。
首先我们看一下左单旋怎么走?
插入数据,更新,接着往上更新。
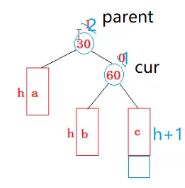
现在我们要进行左单旋,怎么旋转呢?我们现在来实现这个函数,这个函数还是比较复杂的?
首先我们传参需要给parent

左单旋看起来很简单,实际处理起来并不简单。
我们先标一下要动的结点。



现在看起来就是我们的左旋,但是思考思考这个左旋有没有什么问题?
这里最大的问题在哪呢?
第一,我们没有维护parent(不维护parent,肯定是不行的)
b的paren还是指向60,这就乱套了

所以我们的代码还得改:

继续看上面的代码,还有没有什么问题?
这个旋转看起来简单,但是暗藏杀机,稍不注意就搞错了。
subRL可能是空
h==0,subRL就是空
看下面,parent, subR不为空,但是subRL为空

subRL为空,上面的代码就崩了
改一下,不等于空再改,等于空就不动了。
这里还剩一个很大的问题。
你旋转的这棵树不一定是整颗树
因为旋转的这棵树可能是局部的子树
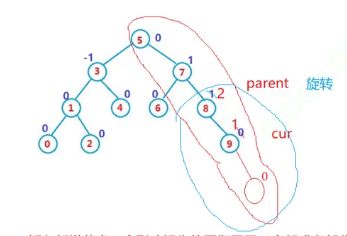
所以基于这样的原因我们还得判断一下,这上面可能还有一个结点

如果30是根,新的根就是60
如果30不是根,那就要更新这个结点。这个结点还是指向30的,这棵树就变成下面这样 了,
这棵树就出问题了

这种情况,我们先把parent保存起来,不然等下就找不到了。
我们分两种方式来改:
1.ppnode为空,说明它就是根,因为一颗二叉树里面只有根节点没有父亲。
这里要注意一下,subR的panret是指向30的,把它旋转了,还是指向30,这里得更新一把。
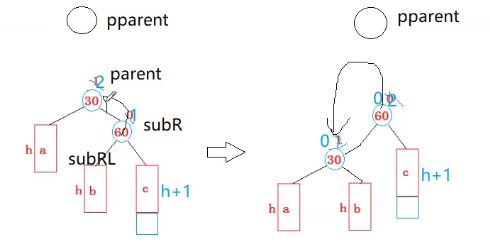
最后更新一下平衡因子

我们之前说过,三叉链是要付出代价的,因为你除了要更新左右还要 更新parent
但是它也带来了便利,因为没有parent就找不到,就找不到ppnode,跟上一层的链接还会更麻烦。
所以我们的一切都是在做一件事情,除了更新左右还有parent。
parent的平衡因子一定为0,为什么?
这个抽象图看起来是非常清楚的,因为影响平衡因子的是左右子树的高度。
void RotateL(Node* parent)
{
Node* subR = parent->_right;
subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* ppnode = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (ppnode == nullptr)
{
_root = subR;
_root->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = subR;
}
else
{
ppnode->_right = subR;
}
subR->_parent = ppnode;
}
parent->_bf = subR->_bf = 0;
}
右单旋代码
右单旋大家可以自己先写一下,旋转是我们AVL树最重要的,
后面红黑树也有旋转。
注意,每改一个结点,都把它的parent改一下
OK和上面一样,我们这里要再做改善,parent不一定是原来的根。

这里我们换一种方式去比较。
最后要注意,不要忘记更新平衡因子。

void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* ppnode = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (parent == _root)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = subL;
}
else
{
ppnode->_right = subL;
}
subL->_parent = ppnode;
}
subL->_bf = parent->_bf = 0;
}
那我们什么时候来调用这两个旋转呢?
我们仔细观察就会发现:

还有两种旋转我们等下再考虑。
这块旋转还是很复杂的,我们对照着仔细看一下
这块最重要的不是代码,大家一定要把图画一遍,把图画一遍这是非常重要的。
双旋
双旋听起来很复杂,其实没那么复杂。
双旋就是两个单旋,但是双旋也有让你感觉头疼的一些情况
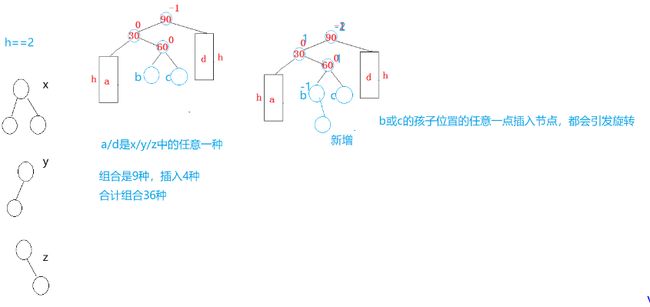
还是跟刚才一样,这是一个抽象图,我们要把它分析成具象图
我们先来分析第一种双旋的情况:
其实大家可以看到,单旋它是一根直线,单纯的一边高

双旋就更复杂一些
a,b,c,d都是空,b,c就不存在了,甚至60都不存在
60是新增
什么时候会引发旋转呢?
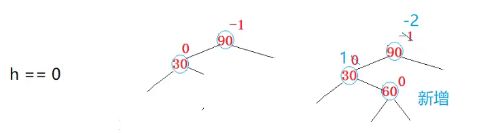

a插入就是单纯的左边高,是单旋。
现在知识b,c插入。
这个旋转终究引发的点在哪呢?
b,c的位置发生变化就会引发旋转。
这个旋转有个很恶心的点,我们上面的单旋已经解决不了这里的问题。
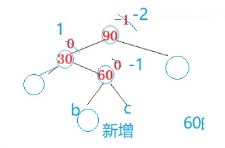
如果我们按上面的单旋玩不转。
看,-2是左边高,如果我们往右旋,不起作用。

从形状来说,双旋是一个折线形状,整体是左边高,但是30这个轴点又是右边高


没有平衡,左边的高度是1,右边的高度是3.
就是换了一个方向的问题,所以单旋解决不了这里的问题
所以这里要用一个双旋来解决问题。
如何双旋呢?
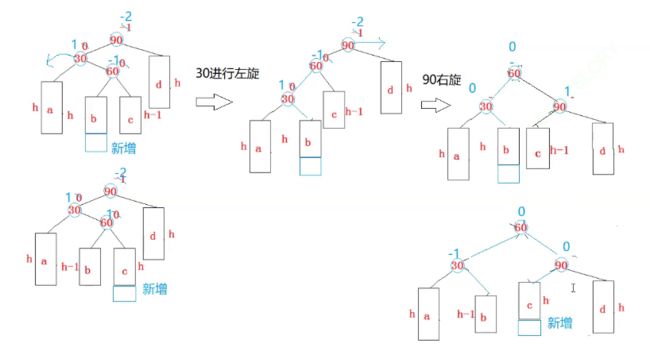
这块涉及平衡因子更新,我们分开来画。
我们先进行一个左旋,对30的位置左旋。

旋转完之后会发现这个图好熟悉,就是一边高。


旋转不需要我们自己写了
左右双旋
从双旋最终的结果来看,把60推上去做根,60的左右分给了30和90,b,c分给了30和90的左边右边。
但是双旋这里最最最复杂的是平衡因子的调节
这三个位置不都是0,也不是把它们更新为-1
它们跟单旋,单旋是旋转完之后,那两个平衡因子一定为0.
那现在问题来了,我们怎么知道是在b插入还是c插入呢?
如何识别?在b插入60bf就是-1,c插入60bf就是1,好像就能识别这里的情况。
但是还有一种情况,不是在b,c插入,看如果h是0,它是什么情况。
如果60本身就是新增,60的平衡因子就是0.
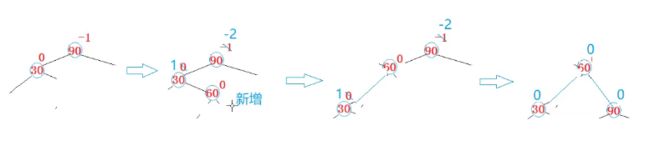
这三种情况的旋转是一样的,但是平衡因子的更新是不一样的。
怎么看它的平衡因子?
我们先记录下来,不然等下不好更新。

我们看subLR的平衡因子就可以了。
因为旋转之后它都会把这些结点的平衡因子变为0,所以我们提前记录一下subLR的平衡因子。

void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == 1)
{
parent->_bf = 0;
subLR->_bf = 0;
subL->_bf = -1;
}
else if (bf == -1)
{
parent->_bf = 1;
subLR->_bf = 0;
subL->_bf = 0;
}
else if (bf == 0)
{
parent->_bf = 0;
subLR->_bf = 0;
subL->_bf = 0;
}
else
{
assert(false);
}
}
右左双旋
右左双旋,大家得对照着画图一点点分析,跟上面的逻辑和过程完全是一摸一样的。
我们先简单的把大框架写出来。

这里的过程是一样的,我们得去看subRL的平衡因子,
有可能是1,-1,0;

这里只画了在c新增,有可能在b新增,有可能60就是新增,大家都要画出来。
待更新

我们为什么要画抽象图呢?
因为它代表无数多种情况。


在60的左右新增都会引发旋转,也就是说,整体而言,都是60这棵树的高度变化
引发了要更新90,90再要更新30,30的这个位置就要进行旋转。
h等于2就更复杂一些。

这些情况是无穷无尽的,我们不能针对具体情况分析,针对具体情况分析你就坏了,
你就处于被动的局面,所以我们要把这些情况进行分析和总结。
这里我想带大家进一步看到的是,不管h0,h1,h==2,它们做的动作都是一样的,
双旋的操作都是一样的,先对90进行右单旋,在对30进行左单旋,就搞定了。
单旋把平衡因子搞成0是不太合适的
下一步我们要对平衡因子进行具体的分析。
这里有三种情况:

如果60自己身就是新增,它旋转完了之后没毛病。
但是如果在b插入,c插入是要分开对待的。
在这个整个走的过程中,我们要去具体的分析怎么去区分这三种情况呢?
只要针对分析出这三种情况,我们就能看到旋转怎么控制,平衡因子怎么办。
这里的核心就是我们可以去观察60的平衡因子,因为旋转一定
是由60这里引发的,这个位置是根源点,这个位置会引发90更新,30更新,
最终引发旋转

这里想要控制好,我们要记录,因为旋转完之后就不给改了


旋转都有一个特点,旋转变成平衡树的同时,它在降低高度。
所以旋转完之后可以break,因为降低高度它对上一层是不会有影响的
所以它是一个局部的子树,它对上一层没有什么影响,所以旋转完了,就结束了。
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 1)
{
subR->_bf = 0;
parent->_bf = -1;
subRL->_bf = 0;
}
else if (bf == -1)
{
subR->_bf = 1;
parent->_bf = 0;
subRL->_bf = 0;
}
else if (bf == 0)
{
subR->_bf = 0;
parent->_bf = 0;
subRL->_bf = 0;
}
else
{
assert(false);
}
}
测试
下一步,我们要对AVL树进行测试。
这里给大家准备了两种情况,第一组是普通情况,第二种包含一个双旋


然后我们再走一个中序。
![]()

但是这个东西不能说明什么任何东西?
这个东西只能证明是搜索树,搜索距离AVL树还是有距离的。
我们现在要判断一颗二叉树是不是平衡树
怎么判断呢?
在这一块我们还是可以快速去判断的。

我们给上一个结点之后怎么办呢?
我们想要判断当前这棵树是不是一颗平衡树 。
我们只把平衡因子检查一遍是不顶事的,因为平衡因子是你自己更新的,万一你更新错了呢!
所以我们这里就是老老实实求高度。
如果它是一颗空树,肯定是一颗平衡树。
如果它不是空树,我们就求出左树的高度和右树的高度,然后算出它的高度差。

但是当前玩的平衡树的求法不符合条件
看下面一种情况:

这棵树按照刚才的检查,这符合AVL树
但是这里不符合,因为你所有的子树都要检查,你不能把当前树看一下就可以了
AVL树不是要求当前树,它是要求所有的树都要符合规则。
怎么对所有子树都检查呢?
我们可以用递归。
我们再去递归它的左右子树进行进一步的检查,因为每个结点进去的时候继续检查它的子树。

当前这颗树是比较简单的,我们再看另外一个场景。
经过测试也是符合的。
我们还需要做一件事,有没有一种可能,你的AVL树是没问题的,但是你的平衡因子更新的有问题
平衡因子更新错的话,现阶段没问题,后续有问题。我们举个简单的例子。

我们不小心把根的平衡因子更新成了0,这就会引发下一步的问题。
现阶段你去检查这棵树是不是AVL树,你去检查高度,检查不出来有问题。

下面新增一个结点之后,更新平衡因子,这个时候导致你该旋转的时候没有旋转
也可能你不该旋转的时候,你旋转了。
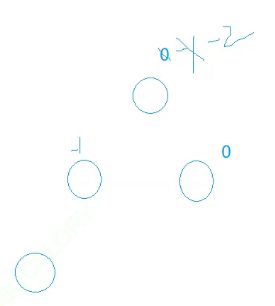
所以平衡因子错误,当前不会爆发问题,后续会爆发很大的问题。
所以我们还得把平衡因子检查一遍。

平衡因子更新错的话,当前树没有问题,后面会爆发很大的问题。
但是这样写就能代表你这颗树是一颗AVL树了吗?
我们刚才上面这样写,并不能说明什么问题。
我们要上一波随机值再来测一下。
待更新
AVL树调试不好调

每次插入要再检查,其实消耗还是挺大的,因为要不断检查这颗树,检查这颗树要用递归还是挺慢的。
我们就最后检查一次吧。

可以多测几次
如果没有出现问题,那这颗树也就没有很大的问题了。
像这种随机插入几万个值,基本上能把所有场景覆盖调。
AVL树还有查找和删除,查找和搜索树是一样的,这里就不写了。
删除就不讲了。我们后面红黑树也是这样。
因为删除的思路和插入的思路基本上是类似的,
还是三个大步骤:
第一,先找到要删除的结点。
第二,更新平衡因子。
第三,看是否需要旋转。
但是删除的过程是要比插入更复杂一些些的。
另一个我们需要注意的是,我们学习AVL树,红黑树的目的,
不是为了工作的时候要手撕红黑树,不是这样的。
这么说吧,大多数的数据结构我们学习它都只是了解,
可能以后我们会自己写一个链表,甚至自己写一个红黑树,
但是99%我们都不可能手撕这颗树,因为你手撕的可能不靠谱,在有些细节上面。
库里面都有,也有很多很成熟的。
我们学习它的意义是,我们要了解它是如何做到平衡,
如何控制住它的效率的。
待更新
AVL树的性能
AVL树的性能是很接近满二叉树的,它就最后一两层缺了一点点。
更严格说,它的形状上有点像完全二叉树,只是完全二叉树要最后的结点是从左到右连续的,
它不是,但是它缺的结点几乎可以忽略不计。
所以它的高度就是logN,增删查改的效率都可以达到logN,这个效率都已经非常高了。
因为10亿个结点你查找一个值最多才三十次。